неравенства »

решите неравенство с дробями

  • решите неравенство x-(5x/2+x дробью)≥0


    Решение: x-(5x/2+x дробью)≥0

    зводим до спільного знаменника 

    x множим на (х + 2 )

    2х + х квадрат - 5х ≥ 0

    х квадрат - зх  ≥ 0 

    Д= 9 - 4 помножити на 1 і 0 = 9 = 3 в квадраті

    хперше 3+3/ 1 = 6 не задовольняє нерівність

    х друге 3-3 /1 = 0

    отже, 0 ≥ 0

    відповідь: квадратна дужка 0 до + нескінченності - кругла дужка

  • 1)11/x+5=11/5(дробью) 2)найти значение выражения 1/7x-7x+2y/14xy(дробью) при x = корень из 10, y=1/2
    3)решить неравенство x в квадрате-4x-12 меньше 0


    Решение: 1.накрест перемножаем числа и получается:
    11*5=11(х+5)
    55=11х+55
    11х=0
    х=0
    ответ:0
    3. 1)задаем функцию.
    у=х²-4х-12
    2)Область определения функции R,т.е. все действительные числа
    3)находим нули функции: у=0; х²-4х-12=0
      D=4+12=16
      х1=2+4=6
      х2=2-4=-6
    4) наносим полученные числа на прямую. ответ получается промежуток (-2;6)

     

  • Решите неравенство дробь: 3x-1/3x+1<=0


    Решение: 3х-1=< 0 3x+1=<0
    3x=<1 3x=<-1

    x,=<1/3 x..=<-1/3

    Не верно предыдущее решение.
    нужно писать 2 системы
    3х-1>=0. 3х-1<=0
    3х+1<0. 3х+1>0

    3х>=1. 3х<=1
    3х<-1. 3х>-1

    х>=1/3. х<=1/3
    х<-1/3. х>-1/3
    ответ (-1/3;1/3]
    скобки и знаки должны быть как написано

  • Решите неравенство /-дробьx+3/x-5 < 0


    Решение: Решаем неравенство методом интервалов.
    Находим нули функции у=    (x+3)/(х-5)
    x+3=0
    х=-3
    Находим нуль знаменателя
    х-5=0
    х=5
    Отмечаем точки на числовой прямой пустым кружком (здесь это круглые скобки) и расставляем знаки :  + - +
    при х =10 получаем (10+3)(10-5)>0
    поэтому на интервале, содержащем точку (10), ставим знак "плюс", далее знаки чередуем. 
       +  _  +
    -------------(-3)------------(5)-----------------------

    Ответ: (−3;5)

  • Решите неравенство дробь в числителе 4x в знаменателе x+1 потом + дробь в числителе 6 в знаменателе x²-x-2 потом +1 ≤ 0


    Решение: $$ \frac{4x}{x+1} + \frac{6}{x^2-x-2} +1 \leq 0 $$
    ОДЗ:$$ \left \{ {{x+1 eq 0} \atop {x^2-x-2 eq 0}} \right. $$
    Разложим знаменатель дроби на множители
    $$ 1+ \frac{4x}{x+1}+ \frac{6}{(x-2)(x+1)} \leq 0 $$
    Приводим дроби к общему знаменателю
    $$ 1+ \frac{4x(x-2)}{(x+1)(x-2)} + \frac{6}{(x-2)(x+1)} \leq 0 $$
    Приводим сложение дробей с одинаковыми знаменателями
    $$ 1+ \frac{4x(x-2)+6}{(x+1)(x-2)} \leq 0 $$
    Раскрываем скобки
    $$ 1+\frac{4x^2-8x+6}{(x+1)(x-2)} \leq 0 $$
    Приводим дроби к общему знаменателю
    $$ \frac{(x+1)(x-2)+4x^2-8x+6}{(x+1)(x-2)} \leq 0 $$
    Раскрываем скобки
    $$ \frac{x^2-x-2+4x^2-8x+6}{(x+1)(x-2)} \leq 0 $$
    Приводим подобные члены
    $$ \frac{5x^2-9x+4}{(x+1)(x-2)} \leq 0 $$
    Решаем уравнение
    $$ 5x^2-9x+4=0 $$
      Находим дискриминант
      $$ D=b^2-4ac=(-9)^2-4*5*4=1 $$
      Дискриминант положителен значит уравнение имеет 2 корня
      $$ x_1,_2= \frac{-b^+_- \sqrt{D} }{2a} \\ x_1= \frac{9-1}{2*5} =0.8;x_2= \frac{9+1}{2*5} =1 $$
    Смотрим знаки на промежутке во вложения

    Ответ: $$ (-1;0.8]U[1;2) $$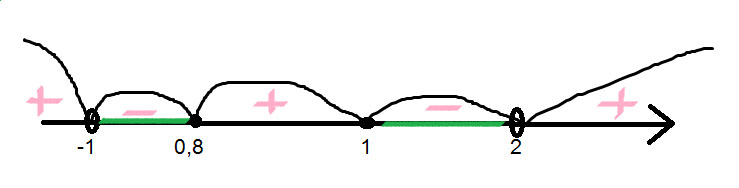

    frac x x frac x -x- leq ОДЗ left x eq atop x -x- eq right. Разложим знаменатель дроби на множители frac x x frac x- x leq Приводим дроби к общему знаменателю frac x x- x x-...
1 2 3 > >>