неравенства »
решить рациональное неравенство
1.Найдите пересечение и объединение множества рациональных чисел и множества действительных чисел.
2.При каких значениях b неравенство bx>6имеет такое же множество решений, что и неравенство x>(6)\(b)
Решение: 1) Q - множество рациональных чисел. R - действительных чисел.$$ Q \cup\ R = R\\Q \cap\ R = Q $$
2) При каких значениях b неравенство bx>6 имеет такое же множество решений, что и неравенство x>(6)\(b)
Если b < 0, то bx>6 тогда, когда x <6/b (покажем это, b = -c, -cx>6, x<-6/c=(6/(-c))=(6/b))
b = 0 рассматриваем, очевидно, остается b > 0.
Рациональные неравенства. Решите неравенства:
$$ (x - \frac{1}{4})(x + 4) > 0 $$
$$ (x - \frac{4}{9})(x - \frac{1}{3}) < 0 $$
Решение: В) (x-1/4)*(x+4)>0
-∞_______+________-4________-______1/4_______+______+∞
x∈(-∞;-4)U(1/4;+∞).
г) (x-4/9)*(x-1/3)<0 4/9≈0,44 1/3≈0,33
-∞________+________1/3_______-________4/9________+_______+∞
x∈(1/3;4/9).Произведение множителей равно нули, когда хотя бы один из множителей равен нулю.
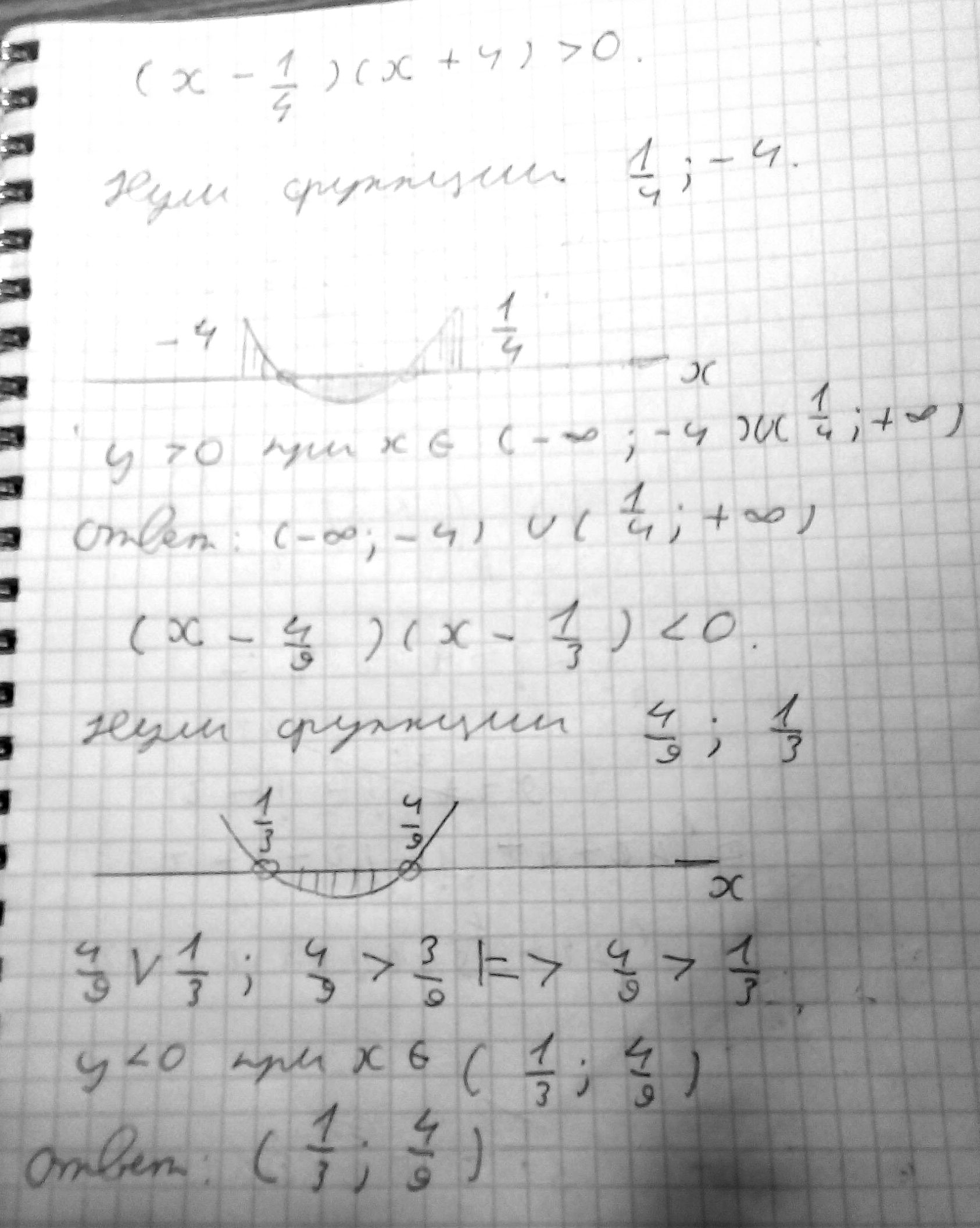
Решение рациональных неравенств $$ \frac{1}{x - 2} + \frac{1}{x - 1} \ge \frac{1}{x} $$
Решение: $$ \frac{1}{x-2} + \frac{1}{x-1} \geq \frac{1}{x} \\ \frac{1}{x-2}+ \frac{1}{x-1}-\frac{1}{x} \geq 0 $$
Приводим дроби к общему знаменателю
$$ \frac{x(x-1)+x(x-2)-(x-2)(x-1)}{x(x-2)(x-1)} \geq 0 \\ \frac{x^2-x+x^2-2x-x^2+3x-2}{x(x-2)(x-1)} \geq 0 \\ \frac{x^2-2}{x(x-2)(x-1)} \geq 0 $$
Рассмотрим функцию
$$ y= \frac{x^2-2}{x(x-2)(x-1)} $$
$$ x(x-2)(x-1)eq 0 \\ x_1e 0 \\ x_2e 2 \\ x_3e 1 $$
$$ D(y)=(-\infty;0)\cup(0;1)\cup(1;2)\cup(2;+\infty) $$
y=0
$$ \frac{x^2-2}{x(x-2)(x-1)}=0 \\ x^2-2=0 \\ x=\pm \sqrt{2} $$
Ответ: $$ x \in [- \sqrt{2} ;0)\cup(1;\sqrt{2}]\cup(2;+\infty) $$
Решите системы рациональных неравенств неравенств 4(9х+3)-9(4х+3)>3(х-2) (х+9)<0
Решение:
−15>3⇒−18>04(9x+3)−9(4x+3)=Раскрытие скобок:36x+12−36x−27=12−27=Приведение подобных:−15
−15>3⇒−18>0
Ответ: x∈∅ , т.е. решений нет.
Т.к. первое неравенство не имеет решений, то и данная система неравенств не имеет решений.Опишите применение метода интервалов для решения дробно-рациональных неравенств
Решение: Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
Метод интервалов позволяет решить его за пару минут.В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.Метод интервалов основан на следующем свойстве дробно-рациональной функции.Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида . Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.Эти точки разбивают ось на N промежутков.Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».

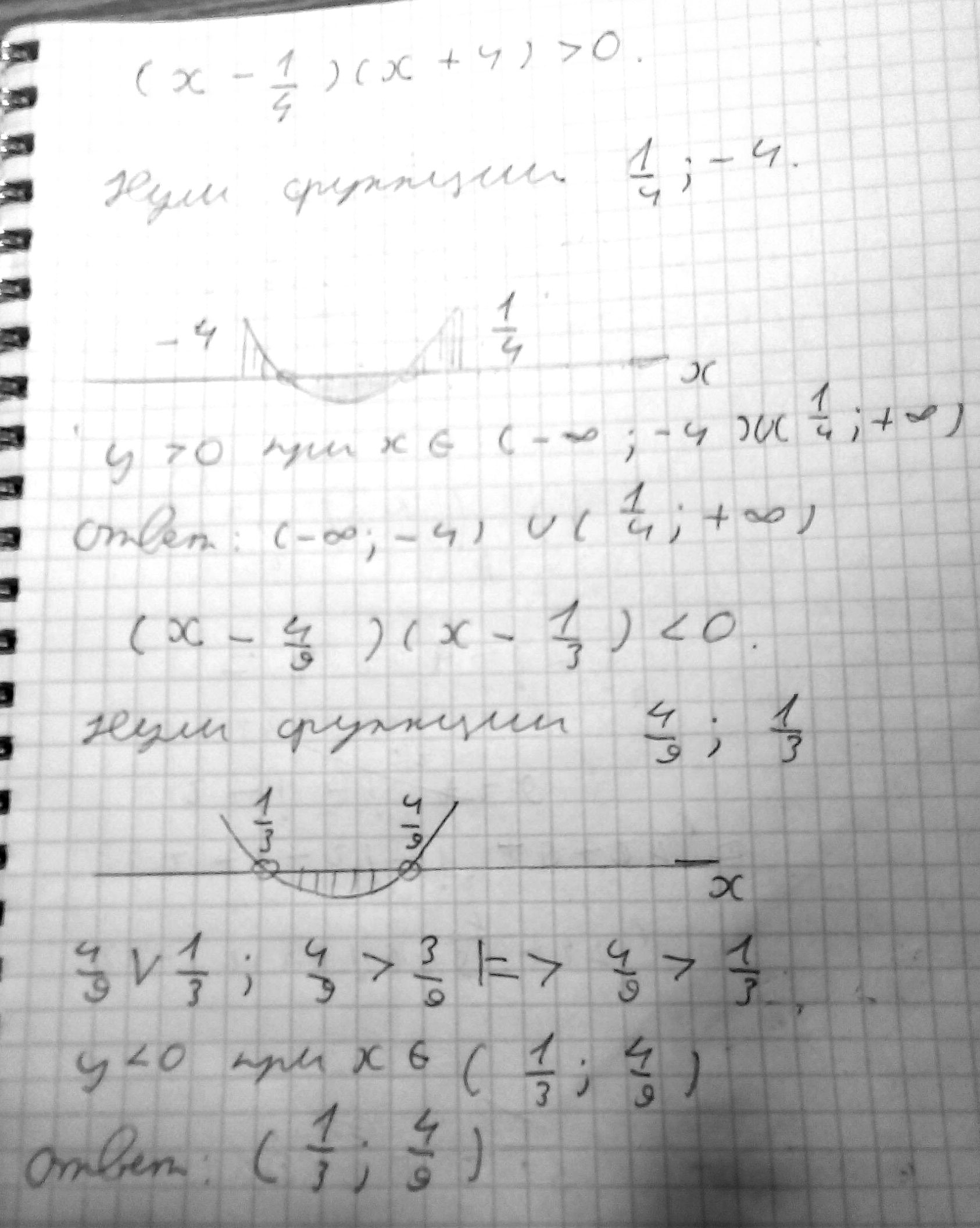

 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...