неравенства »
решить рациональное неравенство - страница 2
Тема: "Рациональные неравенства", решить с пояснениями:
1. (2x-3)(5x+2)>(или =) (2x-3)(3x-8)
2.x^2(x^2-16)<(или =) 9(x^2-16)
Решение:1. (2x-3)(5x+2)≥ (2x-3)(3x-8)
(2x-3)(5x+2)- (2x-3)(3x-8)≥0
(2x-3)(5x+2-3x+8)≥0
(2x-3)(2x+10)≥.
x=1,5 x=-5
x∈(-∞;-5] U [1,5;∞)
2.x^2(x^2-16)≤ 9(x^2-16)
x^2(x^2-16)-9(x^2-16) ≤0
(x²-16)(x²-9)≤0
(x-4)(x+4)(x-3)(x+3)≤0
x=4 x=-4 x=3 x=-3
+ _ + _ +
---------[-4]-------------[-3]----------[3]---------[4]------------------
x∈[-4;-3] U [3;4]
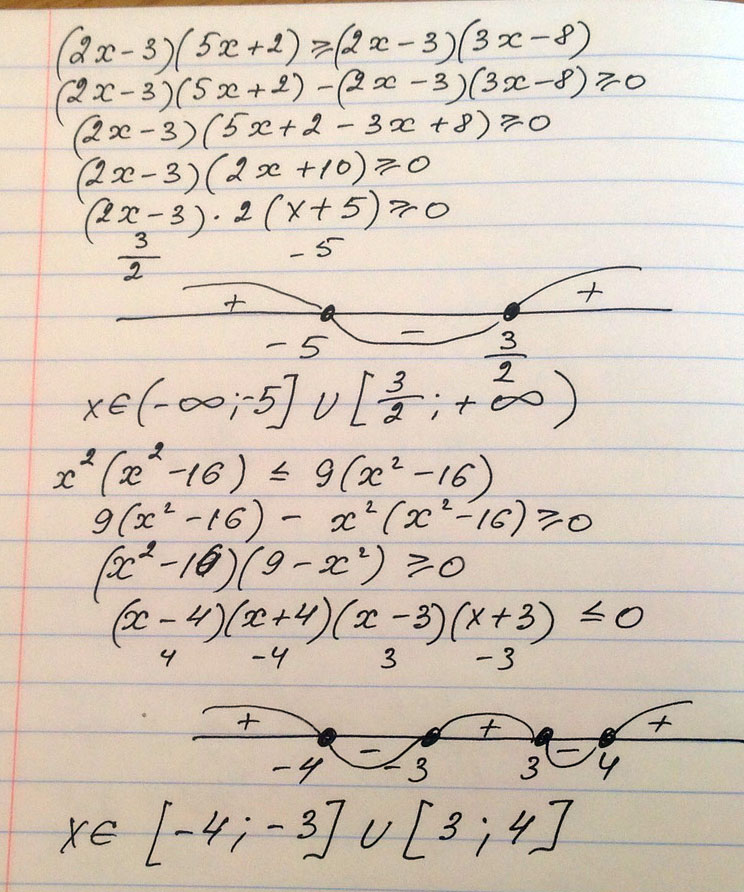
Решите иррациональное неравенство.(х-2)(2х-3)(5-х)≥0
Решение: Все множители приравниваем к 0: x=2 x=1.5 x=5.
Нарисуем числовую прямую (координатную), расставим на ней вычисленные нами точки( наши х), расставим знаки на этой прямой начиная с минуса, тогда
х принадлежит ( - бесконечности; 1.5]U[2;5]. И это не иррациональное неравенство!решите иррациональное неравенство:
корень из икс больше или равно 2
Решение: корень из икс больше или равно 2, то есть решением искомого неравенства будут все числа, квадратный корень из которых будет больше или равен 2. Следовательно, этому условию удовлетворяют числа, находящиеся в промежутке от 4 (включительно) до плюс бесконечности.корень из Х > или = 2
Х > или = 4
ответ: Х = [ 4; + ∞)
Решите иррациональное неравенство $$ x^2 - \sqrt{x^2 - 2x} < 2x + 12 $$
Решение: $$ (x^2-2x)-\sqrt{x^2-2x}-12 < 0 \\ \sqrt{x^2-2x} = t $$
$$ \begin{cases} t \geq 0 \\ t^2-t-12 < 0 \end{cases} < = > \begin{cases} t \geq 0 \\ (t+3)(t-4) < 0\end{cases} < = > \begin{cases} t \geq 0 \\ -3 < t < 4\end{cases} \\ = > 0 \leq t < 4 $$
$$ 0 \leq \sqrt{x^2-2x} < 4 \\ 0 \leq x^2-2x < 16 \\ \begin{cases} x^2-2x \geq 0 \\ x^2-2x -16 < 0 \end{cases} < = > \begin{cases} x(x-2) \geq 0 \\ (x-1+\sqrt{17})(x-1-\sqrt{17}) < 0\end{cases} < = > $$
$$ \begin{cases} x \in (-\infty; 0] \cup [2; +\infty) \\ x \in (1-\sqrt{17}; 1+\sqrt{17}) \end{cases} => \boxed {x \in (1-\sqrt{17};0] \cup [2; 1+\sqrt{17}) } $$
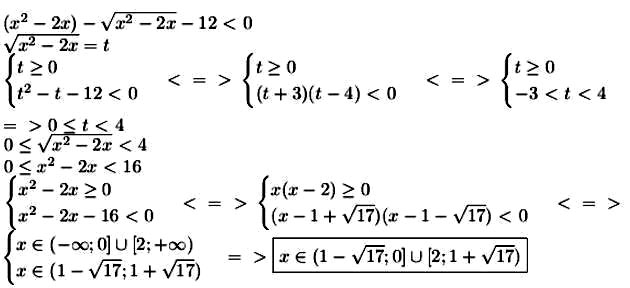
Решить иррациональное неравенство $$ \sqrt{7x+5} = \sqrt{2-3x} $$
Решение: 1) $$ \sqrt{7x+5} = \sqrt{2-3x} $$
ОДЗ: 7x+5≥0 2-3x≥0
7x≥ -5 -3x≥ -2
x≥ -5/7 x≤ 2/3
x∈[-5/7; 2/3]
7x+5=2-3x
7x+3x=2-5
4x= -3
x= -3/4
-5/7 = (-5*4)/(7*4)= -20/28
-3/4 = (-3*7)/(4*7)= -21/28
x=-3/4∉[-5/7; 2/3]
нет решений.
Ответ: нет решений.

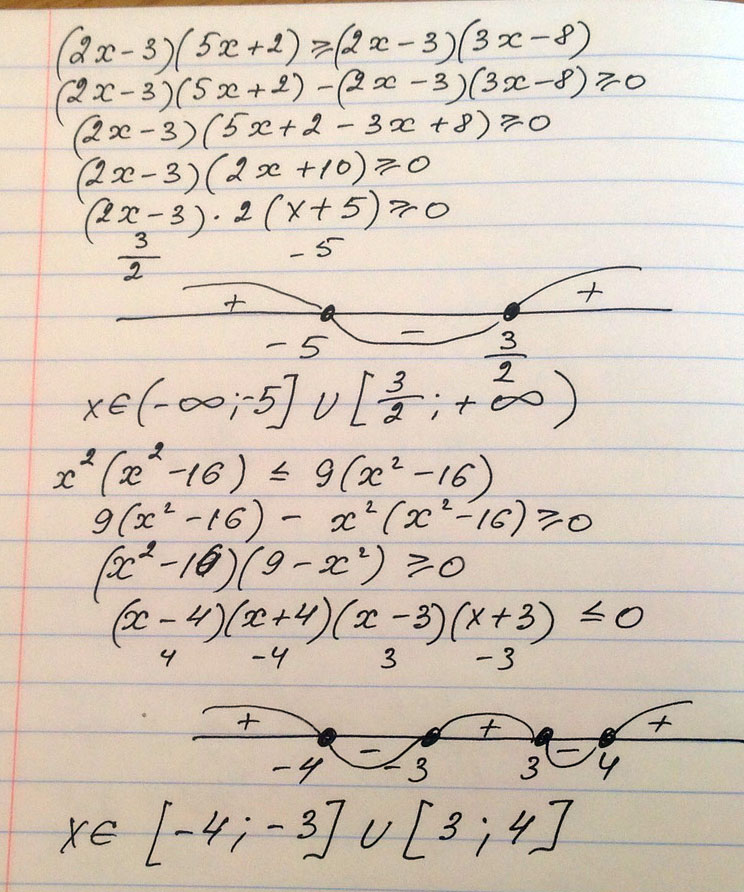
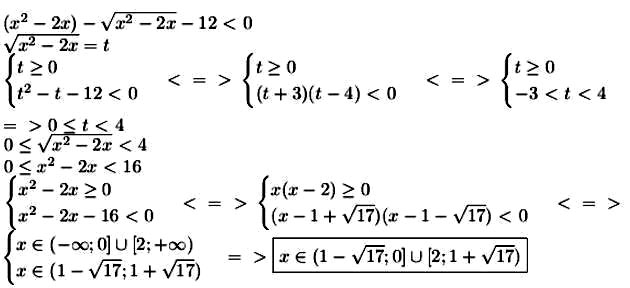
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...