неравенства »
решить рациональное неравенство - страница 3
Решите иррациональное неравенство. $$ \sqrt{x^2-3x+2}<5-x $$
Решение: $$ \sqrt{x^2-3x+2}<5-x;\\ D(f): \left\{{{5-x>0} \atop {x^2-3x+2 \geq 0}}\right. \\ D=9-8=1; x_1= \frac{3-1}{2}=1;x_2= \frac{3+1}{2}=2;\\ \left\{ {{x<5} \atop { \left[{{x\leq1} \atop {x\geq2}} \right. }} \right. \\ x\in(-\infty;1]\bigcup[2;5) x^2-3x+2<(5-x)^2;\\ x^2-3x+2<25-10x+x^2;\\ 7x<23;\\ x< \frac{23}{7}=3 \frac{2}{7} \\ x\in(-\infty;1]\bigcup[2;3\frac{2}{7}) $$Вариант решения во вложении:
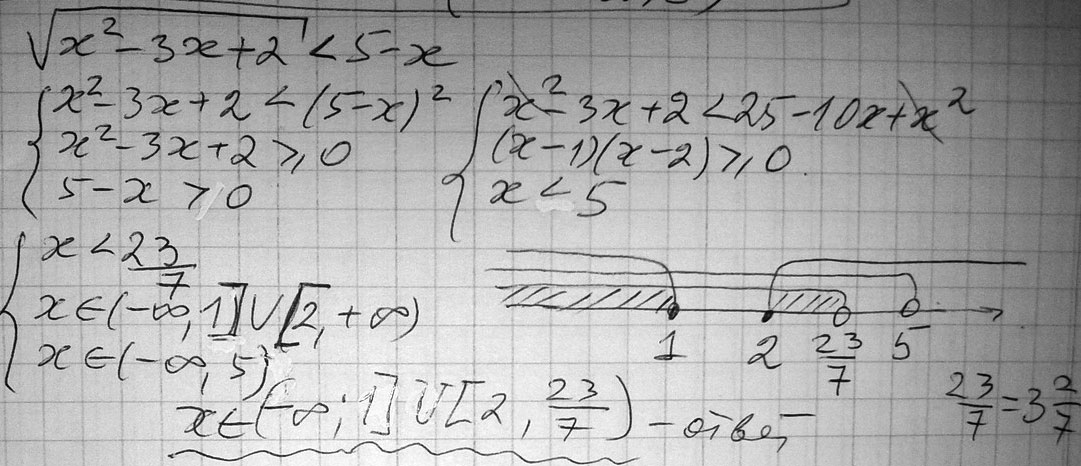
Решите одно иррациональное неравенство $$ 3 \sqrt{x-4}=14-x $$
Решение: Решите одно иррациональное неравенство 3√(x-4) = 14 -x ;
ОДЗ x - 4 ≥ 0 ⇒ x ≥4 .
Если 14 -x ≥ 0 ⇒x ≤ 14 * * * 4 ≤ x≤ 14⇔ x∈[4 ;14] * * *
то :
(3√(x-4 ))² = (14 -x)² ;
9(x-4) = 196 -28x +x² ;
x² -37x +232 =0 ;
x₁ = 8 ∈ [4 ; 14]
x₂ = 29 ∉ [4 ; 14]
ответ: 8 .
Вариант 2
ОДЗ x-4≥0⇒x≥4 U 14-x≥0⇒x≤14⇒x∈[4;14]
9(x-4)=196-28x+x²
x²-28x+196-9x+36=0
x²-37x+232=0
x1+x2=37 U x1*x2=232
x1=8
x2=29∉ОДЗ
Ответ х=8
Решить иррациональные уравнения и неравенство: √х+9= х-3
под корнем х-2= под корнем х^2-4
под корнем 12+х^2<6-х
Решение: V - знак корня
1)V(x+9) =x-3
ОДЗ:
{x+9>=0; x>=-9
{x-3>=0; x>=3
Решение ОДЗ: x>=3
Т.к. обе части уравнения неотрицательны, возведем их в квадрат:
x+9= (x-3)^2
x+9= x^2-6x+9
x+9-x^2+6x-9=0
-x^2+7x=0
x^2-7x=0
x(x-7)=0
x=0; x=7
x=0 нам не подходит по ОДЗ
Ответ:{7}
2)V(x-2)= V(x^2-4)
ОДЗ:
{x-2>=0; x>=2
{x^2-4>=0; x<=-2, x>=2
Решение ОДЗ: x>=2
Возведем в квадрат обе части:
x-2=x^2-4
x-2-x^2+4=0
-x^2+x+2=0
x^2-x-2=0
D=(-1)^2-4*1*(-2)=9
x1=(1-3)/2=-1 - не подходит по ОДЗ
x2=(1+3)/2=2
Ответ:{2}
3)V(12+x^2) <6-x
В левой части неравенства стоит корень,принимающий только неотрицательные значения. Следовательно, и правая часть должна быть положительной.
ОДЗ:
{12+x^2>=0 при x e R
{6-x>0, x<6
Решение ОДЗ: x<6
Возведем в квадрат обе части:
12+x^2<(6-x)^2
12+x^2<36-12x+x^2
12+x^2-36+12x-x^2<0
12x-24<0
12x<24
x<2
С учетом ОДЗ: x <2Решить рациональное неравенство.(x^2+2x-15)(x^2-4x+3)(x-1)≤0
Решение: Квадратные трехчлены разложим на множители:
x^{2} +2х-15 = (х - 3)(х + 5); x^{2} - 4х + 3 = (х - 1)(х - 3);
получим (х - 3)(х + 5)(х - 1)(х - 3)(х - 1) ≤ 0. Решим методом интервалов.
Найдем нули функции: х = 3, х = - 5, х = 1, х = 3, х = 1. Отметим их на оси х, определим знак на каждом интервале, берем промежутки со знаком -, т.к. неравенство ≤ 0. Ответ: [- ∞; - 5] и х = 1, х = 3.РЕШИТЬ РАЦИОНАЛЬНОЕ НЕРАВЕНСТВО : 3/(Х-2)≥Х
Решение: ОДЗ: $$ x eq 2 $$
Переносим в левую часть, решаем уравнение...
$$ \frac{3}{x-2} -x \geq 0 $$
$$ \frac{3- x^{2} +2x}{x-2} \geq 0 $$
Умножаем на -1
$$ \frac{ x^{2} -2x-3}{x-2} \leq 0 $$
$$ \frac{(x+1)(x-3)}{x-2} \leq 0 $$
Решаем методом интервалов.
$$ x=-1,x=3,x eq 2 $$
Отмечаем значения на прямой, интервалы чередуются справа на лево + - + -.
Берём те значения, где -.
То есть ответ: (-бесконечности;-1] и (2;3]

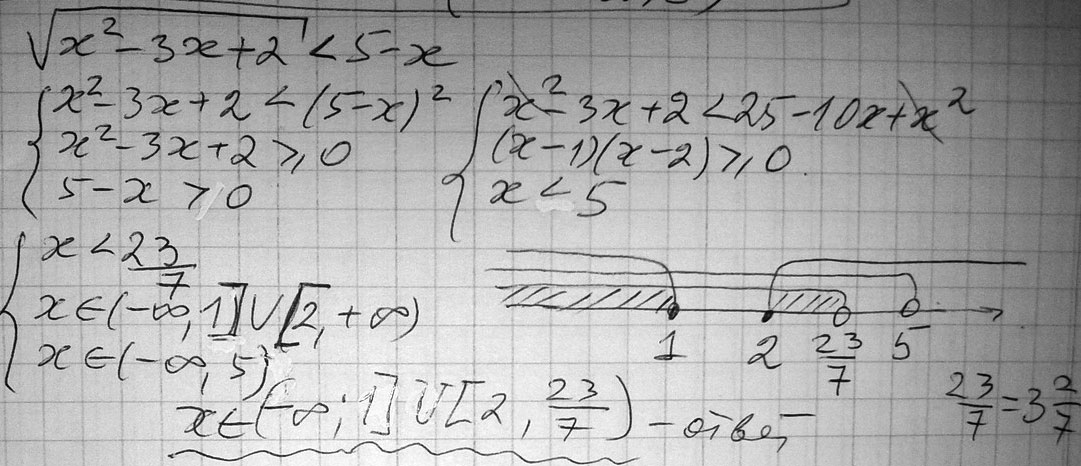
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...