неравенства »

найдите решение системы неравенств

  • Система неравенств. $$ \left\{ {{x^2 - 3 > 0}\atop{2x > 0}} \right. $$


    Решение: Решаем 1 неравенство
    x²-3>0
    (x-√3)(x+√3)>0
    x-√3=0⇒x=√3
    x+√3=0⇒x=-√3
       +  _  +
    --------------(-√3)-----------(√3)------------------
    x<-√3 U x>√3
    Решаем 2 неравенство
    2x>0⇒x>0
    А теперь  находим общее

    ____\__\__\_\_\(-√3)________(0)_________(√3)_/__/__/__/__/____
     
    x∈(√3;∞)

    Второе неравенство означает, что х больше 0
    Первое неравенство означает, что  ему удовлетворяют х принадлежащие двум областям :$$  х < -\sqrt{3} $$  и $$ х > +\sqrt{3} $$.
    Решение системы - это нахождение пересечения областей решений  1-го и 2-го неравенств, т.е. нахождение тех значений х, которые удовлетворяют обоим. 
    Это$$  х > \sqrt{3} $$
     Ответ:$$  х > \sqrt{3}$$

  • найдите множество решения системы неравенств:

    1-2x≤3

    3x+2<1

    это система


    Решение: 1-2x≤3

    -2x≤3-1

    -2x≤2 разделим все на -2

    x> либо равно -1

    3x+2<1

    3x<1-2

    3x<-1

    x<-1/3

    Эти два графика пересекаются, поэтому решения располагаются на интервале от -1 до -1/3

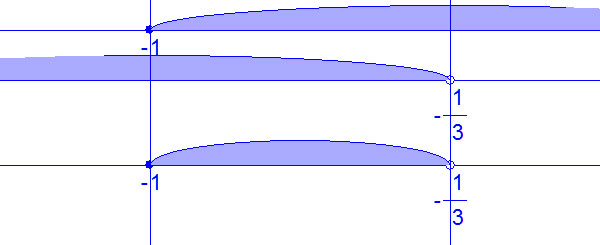
    - x - x - - x разделим все на - x либо равно - x...

  • Для всякого каждого значения a решите систему неравенств: 4(x-a)≤3(2-x); -5x≤a;


    Решение: {4x-4a≤6-3x⇒4x+3x≤4a+6⇒7x≤4a+6⇒x≤(4a+6)/7
    {-5x≤a⇒x≥-a/5
    -a/5≤x≤(4a+6)/7⇒
    -a/5≤(4a+6)/7
    -7a≤20a+30
    -27a≤30
    a≥-30/27
    Ответ при a≥-30/27 х∈[-a/5;(4a+6)/7]

    -----------------------------------------------

    $$ \left \{ {{x \geq -\frac{a}{5} } \atop {x \leq \frac{6+a}{7} }} \right. $$
    Если -a/5<(6+a)/7( то есть если a>-5/2): x∈[-a/5; (6+a)/7]
    Если -a/5>(6+a)/7 (a<-5/2): x∈∅
    Наконец если a=-5/2: x=1/2
    Ответ:
    При a<-5/2 неравенство не имеет решений.
    При a=-5/2: x=1/2
    При a>-5/2: x∈[-a/5; (6+a)/7]

  • Для каждого значения параметра a решите совокупность неравенств: [(7-2x)/5 [x^2+(8+a)x+8a>=0
    $$ \left[ {\frac{7 - 2x}{5} < \frac{x}{1} + 1 \atop x^2 + (8+a)x + 8a \ge 0}\right. $$


    Решение: С квадратным уравнением делаете следующее:
     х^2+(8+a)x+8a≥0 -раскладываете его на множители через теорему Виета:
    x1+x2=-(8+a)
    x1*x2=8a
    Отсюда следует, что x1=-8; x2=-a
    получается: (x+8)(x+a)≥0
    Это после решения 1 примера в задании, в этом 1-ом примере получите область значения "x", т.е. его интервал значений, а он получается x>2/7, а значит он положительный, т.е. (x+8) - всегда положительно, то и (x+a) всегда имеет положительный ответ.
    Получается: x+a≥0, возьмём минимум "x", берётся 2/7, хоть оно и со строгим знаком 2/7 + a≥0 , ответ: a∈[-2/7;+∞)

  • Решите систему неравенств

    3(x-2)-(2x-1)>5-2x4(x+2)-6(x+1)<6+x

    Решите двойное неравенство


    x-6 x-3 x+7
    ___ < ___ < ______
    9 4 24


    При каких значениях параметра a система неравентсв не имеет решений


    { 5-3x<4x-2
    2+3x<2a+2x

    Найдите целые решения системы

    { 3x(в квадрате) - 12x+9<0
    6x-5>0


    Решение: 3(x-2)-(2x-1)>5-2x

    3x-6-2x+1>5-2x

    3x>10

    x>10/3

    4(x+2)-6(x+1)<6+x

    4x+8-6x-6<6+x

    -3x<4

    x>-4/3

    x-6 x-3 x+7
    ___ < ___ < ______
    9 4 24

    x-6/9<x-3/4

    4x-24<9x-27

    3<5x

    x<3/5

    x-3/4<x+7/24

    24x-72<4x+28

    20x<100

    x<5

1 2 3 > >>