неравенства »
решить логарифмическое неравенство - страница 10
2log2(x)<2-log2(x+3) решите логарифмическое неравенство
Решение: 2*log₂x<2-log₂(x+3)
log₂x²+log₂(x+3)<2
log₂(x² *(x+3))<2. 2=log₂2²=log₂4
log₂(x³+3x²)<log₂4
a=4, a>1 знак неравенства не меняем
ОДЗ:
$$ \left \{ {{x\ > \ 0} \atop {x+3\ > \ 0}} \right. \left \{ {{x\ > \ 0} \atop {x\ > \ -3}} \right. $$
x∈(0;∞)
x³+3x²<4
x³+3x²-4<0
x=1, x=-2 корни уравнения x³+3x²-4=0
(x-1)*(x+2)*(x+2)<0
метод интервалов:
- +
-(-2)-(0)->x
x∈(-∞;-2)∪(-2;0)
учитывая ОДЗ (x>0), получим: решений нет
Решить логарифмическое неравенство \(\frac{1}{5-\lg x} + \frac{2}{1+\lg x} < 1\)
Решение: Там вроде 1/5-lgx+2/1+lgx=1, т. е =1.
x>0;x≠10^5;x≠0,1
(1+lgx)+2(5-lgx)=(5-lgx)(1+lgx)
1+lgx+10-2lgx-5-5lgx+lgx+lg²x=0
lg²x-5lgx+6=0
lgx=a
a²-5a+6=0
a1+a2=5 U a1*a2=6
a1=2⇒lgx=2⇒x=100
a2=3⇒lgx=3⇒x=1000
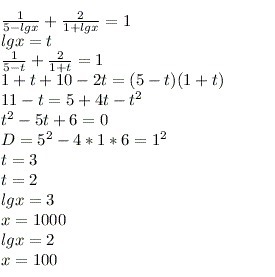

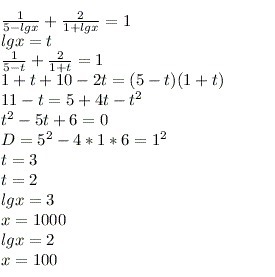
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...