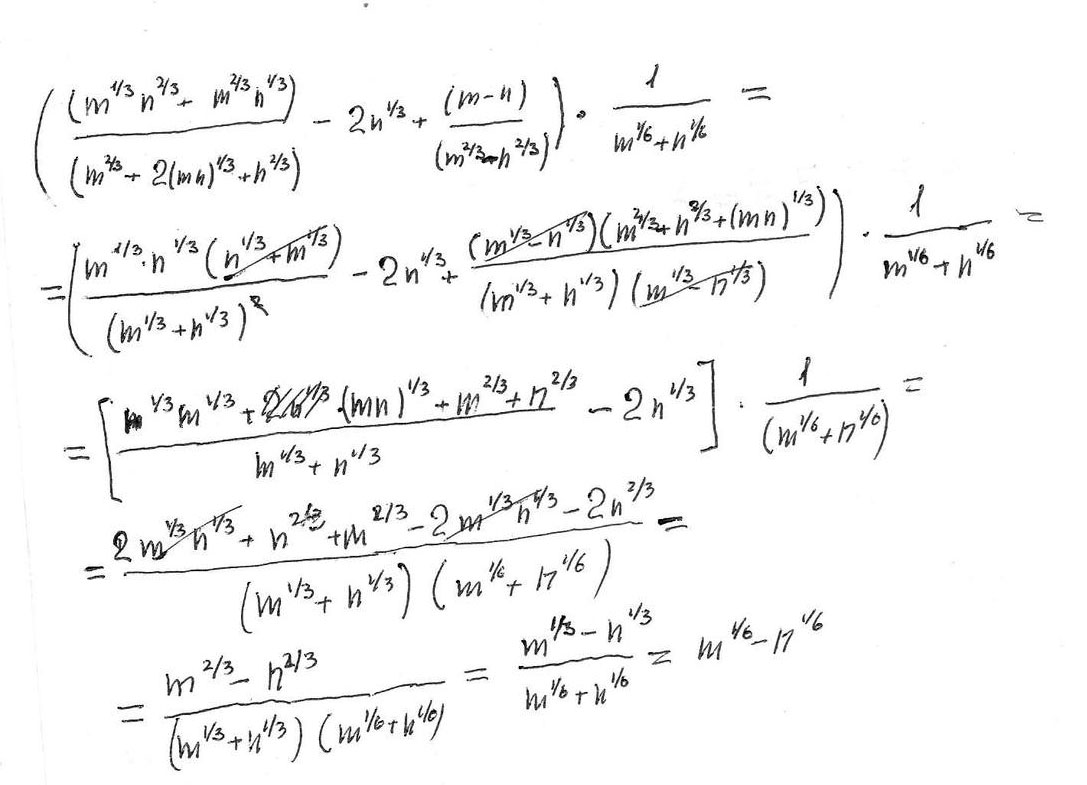степени »
степень корня
Уравнение log (х+5) по основанию 3=4-log(3x+1) по основанию 3
Вычислить. Log (36√6 над корнем степень 4)по основанию 6
Решение: $$ \log_3(x+5)=4-\log_3(3x+1) $$
Перенесем все логарифмы в лево:
$$ \log_3(x+5)+\log_3(3x+1)=4 $$
По свойству:
$$ \log_3(x+5)(3x+1)=4 $$
Откуда:
$$ 3^4=(x+5)(3x+1) $$
$$ 81=3x^2+16x+5 $$
$$ 3x^2+16x-76=0 $$
$$ \sqrt{D}= \sqrt{1168}=4 \sqrt{73} $$
$$ x_{1,2}= \frac{-16\pm4\sqrt{73} }{6}= \frac{-4(4\pm \sqrt{73}}{6}=- \frac{2(4\pm \sqrt{73})}{3} $$
2)
$$ \log_6(36 \sqrt[4]{6})=\log_636+ \frac{1}{4}\log_66=2+\frac{1}{4}=2,25 $$
Боковая сторона и меньшее основание равнобедренной трапеции, вписанной в окружность, стягивают дуги по 60 градусов. Найти площадь трапеции, если её высота равна 4 корня 4 степени из 3
Решение: ABCD вписанная равнобедренная трапеция, \( ВH= 4 \sqrt[4]{3} \) -высота.
Поскольку меньшее основание и боковые стороны стягивают дуги по 60 градусов, радиусы, соединяющие центр окружности с вершинами при меньшем основании трапеции, равны этому основанию.Вместе они стягивают дугу 180гр. Значит и большее основание стягивает дугу 180гр,тогда большее основание равно 2 радиусам.
\( AH=R/2=BH/sinA= 4 \sqrt[4]{3} : \sqrt{3} /2=4 \sqrt[4]{3}*2/ \sqrt{3} =8/ \sqrt[4]{3} \)
\( BC=R=16/ \sqrt[4]{3} \), \( AD=2R= 32/ \sqrt[4]{3} \)
\( S=(BC+AD)*BH/2 \)
\( BC+AD=3R= 48/ \sqrt[4]{3} \)
\( S=48/ \sqrt[4]{3} *4 \sqrt[4]{3} /2=96 \)(( ∛mn² + ∛m²n) / ( ∛m² + 2∛mn +∛n²) - 2∛n + (m-n) / (∛m²- ∛n²) ) * 1/ (√m +√n) решить (√m +√n) в этом выражении оба √ (корня) в 6 степени
Решение: M^(1/6)-n^(1/6); решение в файле.................
1)( ∛mn² + ∛m²n) / ( ∛m² + 2∛mn +∛n²) - 2∛n + (m-n) / (∛m²- ∛n²) =
=∛mn(∛n+∛m)/(∛m+∛n)² - 2∛n +(∛m-∛n)(∛m²+∛mn+∛n²)/(∛m-∛n)(∛m+∛n)=
=∛mn/(∛n+∛m) - 2∛n +(∛m²+∛mn+∛n²)/(∛m+∛n)=
=(∛mn-2∛mn-2∛n²+∛m²+∛mn+∛n²)/(∛m+∛n)=(∛m²-∛n²)/(∛m+∛n)=
=(∛m-∛n)(∛m+∛n)/(∛m+∛n)=∛m-∛n
2)(∛m-∛n)*1/($$ \sqrt[6]{m} + \sqrt[6]{n})=\\=( \sqrt[6]{m} + \sqrt[6]{n})(\sqrt[6]{m} - \sqrt[6]{n})/(\sqrt[6]{m} + \sqrt[6]{n}) = ( \sqrt[6]{m} - \sqrt[6]{n}) $$
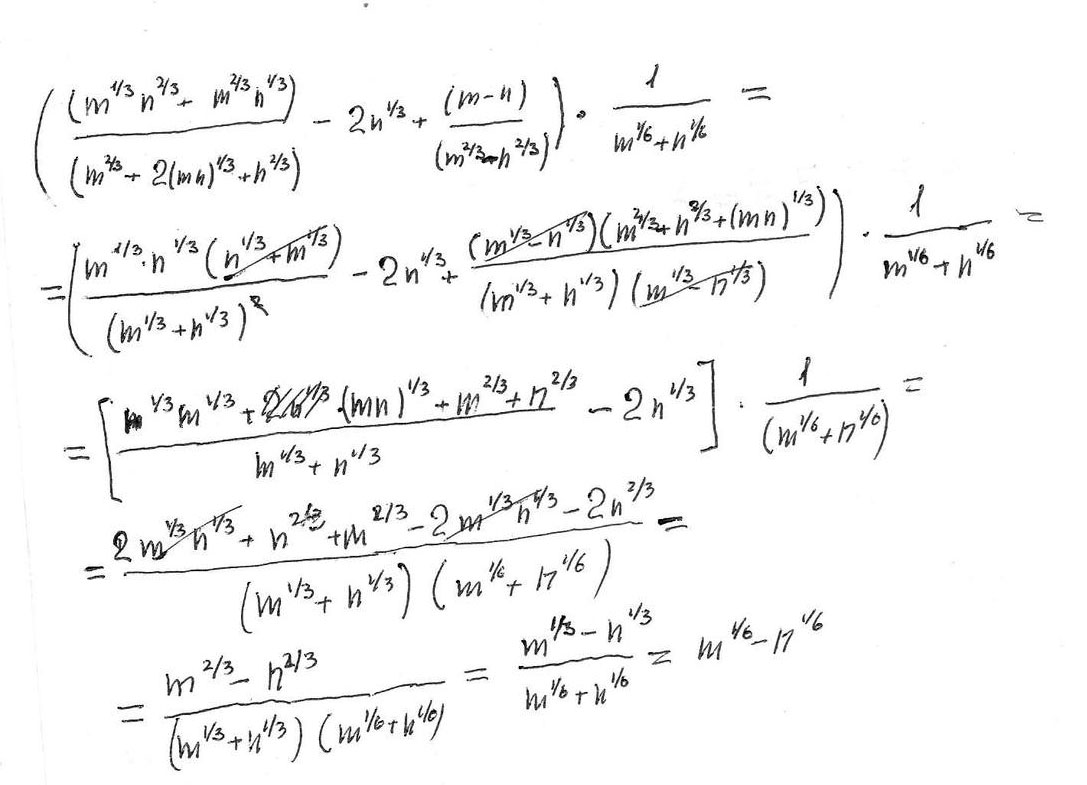
Объясните, почему уравнение не имеет корней:1) x(2 степень )= - 1
2)|x| = - 5
3) x (6 степень ) + 1 = 0
4) |x| + 10 = 0
Решение: 1) Любое число, возведенное в четную степень (включая квадрат), - положительное.
2) Модуль числа не может быть отрицательным.
3) Число, возведенное в четную (6) степень, - положительное. Любое положительное число + 1 = положительное, но точно не ноль.
4) Модуль числа - положительное число. + 10 = положительное, но не ноль.Как преобразовать, \( 0,3^{\sqrt{5}} \) чтоб не было корня из пяти в степени?
Решение: Даны числа: 0,3^9; 1; 0,3^-корень из пяти; 0,3^1/3; 0,3^-9; 0,3^1/3
Располагаем:
0,3^9
0,3^1/2
0,3^1/3
1
0,3^-корень из пяти
0,3^-9
так как под отрицательной степенью получить число больше единицы, то число 1 между положительными и отрицательными степенями!
Располагаем числа больше просто по степеням, поскольку основание одно, его надо не забывать, что в данном случае числа в отрицательной степени, будут больше положительных, так как снизу стоит дробь!
Поэтому просто ориентируемся на степени!
Так как число 0,3 в любой степени меньше 1