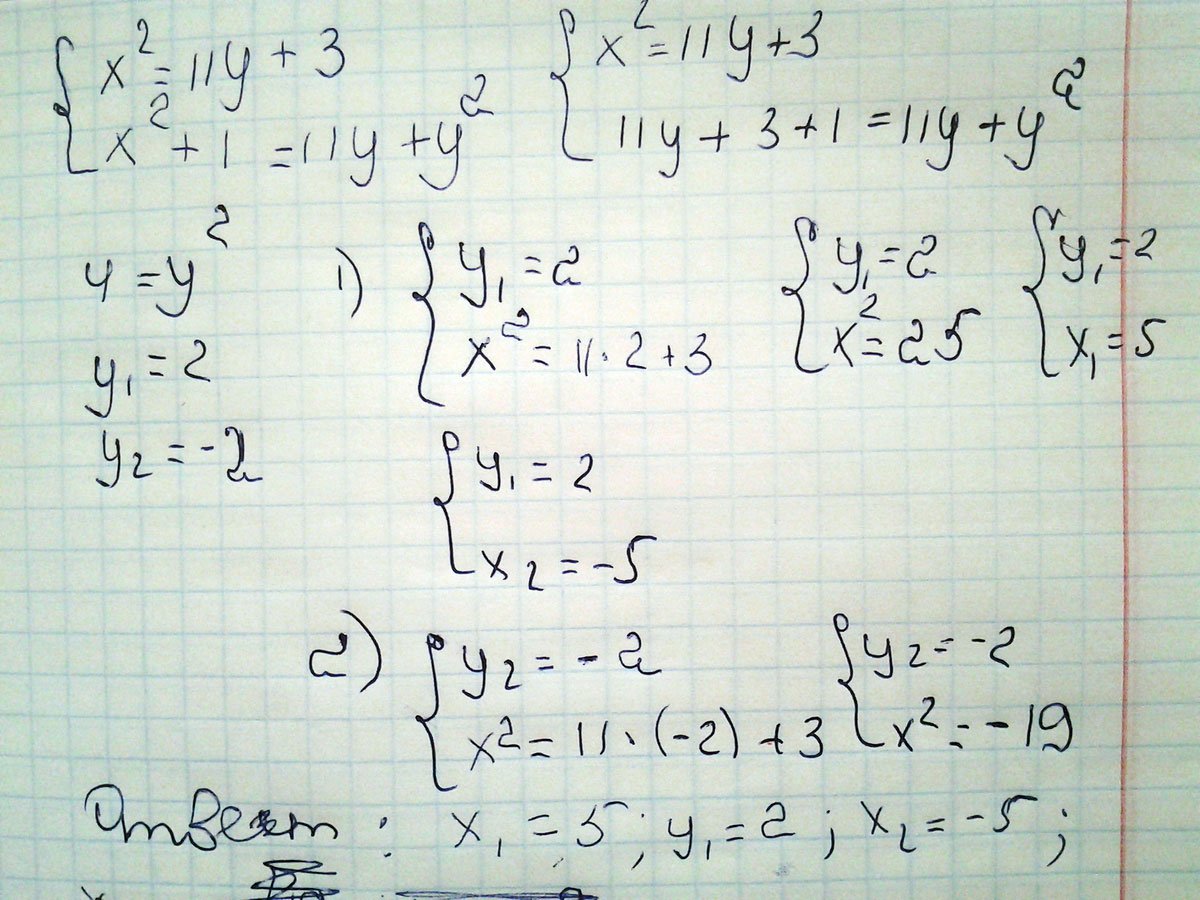степени »

возведение степени в степень - страница 3

  • Решить систему уравнений х^2=11у+3 х^2+1=11у+у^2 (кстати ^ знак возведения в степень)


    Решение:

    Из первого уравнения х2 = 11у + 3 подставляем х2 во второе уравнение получаем
    11у + 3 + 1 = 11у + у2 сокращаем
    получаем у2 = 4
    у = 2
    подставляем в первое уравнение получаем
    х2 = 25
    х = 5
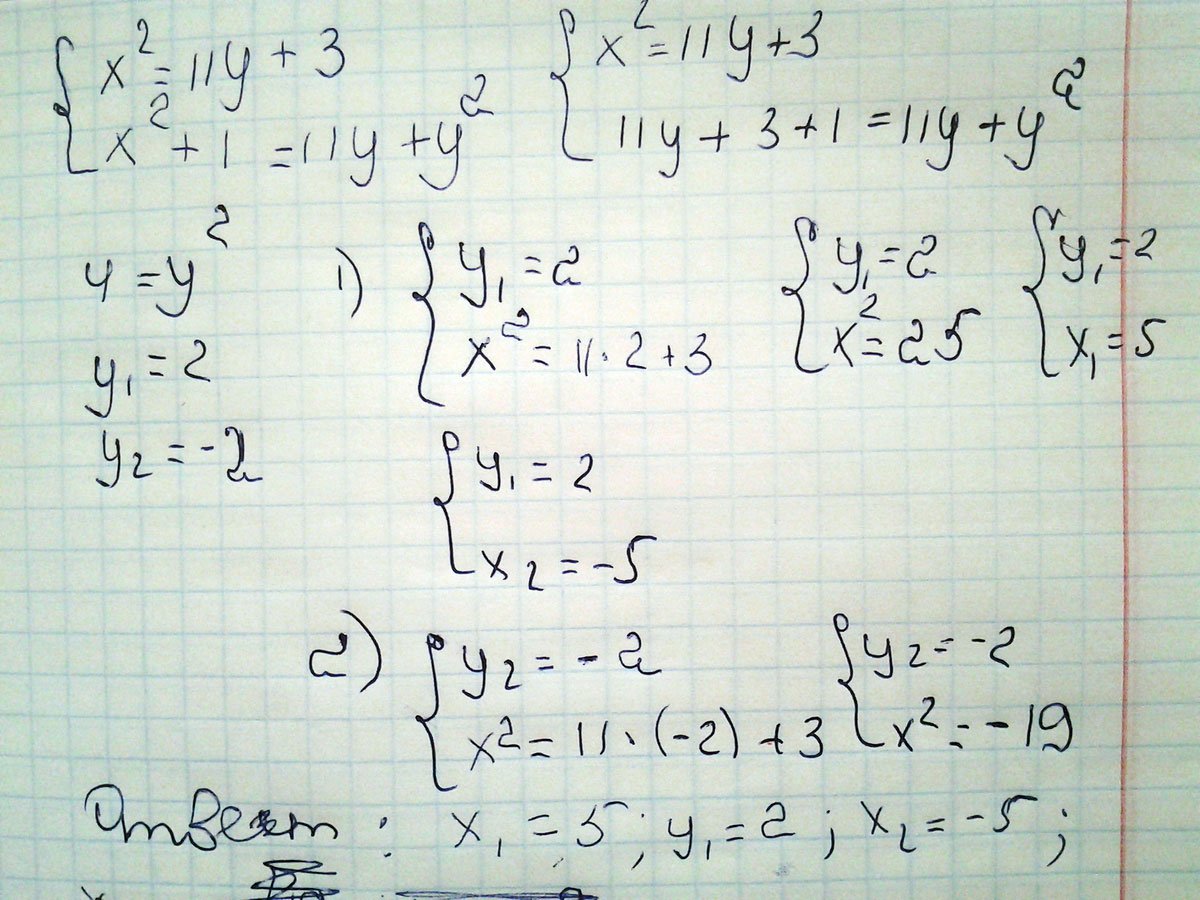
    Из первого уравнения х у подставляем х во второе уравнение получаем у у у сокращаемполучаем у у подставляем в первое уравнение получаемх х...

  • А) (а-5)(а+5)(а^2+25) б) (3.5р-1.2k)(3.5р+1.2k)
    в) (1.7s+0.3t^2)(0.3t^2-0.3t^2)
    г) (m-1)(m^3+m^2+m+1)
    ^-возведение в степень


    Решение: А) (а - 5)(а +5)(а² + 25) = (а² - 25)(а² +25) = а⁴ - 625
    б)(3,5р - 1,2k)(3,5p + 1,2k) = 12,25p² - 1,44k²
    в) (1,7s + 0,3t²) (0,3t² - 1,7s) = 0,09 t⁴ - 2,89s²
    г) (m - 1)(m³ + m² + m + 1) = m⁴ + m³ + m² +m - m³ - m² - m - 1 = m⁴ - 1

    Воспользуемся формулами сокращённого умножения: a) (a^2-5a+5a-25)(a^2+25)=(a^2-25)(a^2+25)=a^4-25^2; б) (3,5p-1,2k)(3,5p+1,2k)=3,5^2 умножить на p^2-1,2^2 умножить на k^2; в) (1,7s+0,3t^2)(0,3t^2-0,3t^2)=(1,7s+0,3t^2) умножить на 0 = 0; г) (m-1)(m^3+m^2+m+1)=(m^4-1)+(m^3-1)+(m^2-1) — .....???

  • Выполните возведение одночлена в степень: (6у)³ =
    (5х⁵у³)³=
    (-1/3ху)⁴=
    (-а²b³c)⁴=
    -(3m²n³)⁴=
    -(-3m²n³)⁴=
    -(-x³yz²)⁴=


    Решение: 1)6³у³= 216у³

    2)125х¹⁵у⁹

    3)1/81х⁴у⁴

    4)а⁸b¹²c⁴

    5)-81m⁸n¹²

    6)-81m⁸n¹²

    7) - x¹²y⁴z⁸

  • доказать тождество
    (a^3 - b^3) ^3 - (a^3 + b^3)^3 + 6a^6b^3 = - 2b^9
    ^ - это возведение в степень


    Решение: $$ (a^{3}- b^{3} )^3 - (a^{3}+b^{3} )^3 + 6 a^{6}b^3 = \\ =-2b^3((a^3-b^3)^2+(a^3-b^3)(a^3+b^3)+(a^3+b^3)^2) +6a^6b^3= \\ -2b^3(a^6-2a^3b^3+b^6+a^6+a^3b^3-a^3b^3-b^6+a^6+2a^3b^3+b^6) \\ +6a^6b^3 =\\ 6a^6b^3-2b^3(3a^6+b^6)= \\ 6a^6b^3-6a^6b^3-2b^9=-2b^9 $$

  • Что такое операции выполнимые на множестве натуральных чисел, целых чисел, рациональных чисел (все связанное с делением, сложением, вычитанием, умножением и возведением в степень)


    Решение: Для натуральных чисел +, x, возведение в степень.
    для целых чисел +, х, возведение в степень.
    Целые числа — расширение множества натуральных чисел {N}, получаемое добавлением к {N} нуляи отрицательных чисел вида {-n}. Множество целых чисел обозначается {Z}. Необходимость рассмотрения целых чисел продиктована невозможностью, в общем случае, вычесть из одного натурального числа другое — можно вычитать только меньшее число из большего.
    Рациональное число (лат. ratio - отношение, деление, дробь) - это число которое может быть представлено в виде дроби, где числитель  - целое число, а знаменатель  - натуральное. Множество рациональных чисел  обозначается (от англ. quotient "частное") и может быть записано в виде:. Числа вида - называют еще обыкновенными дробями. Если, то дробь называется правильной, если, то - неправильной.

<< < 123 4 > >>