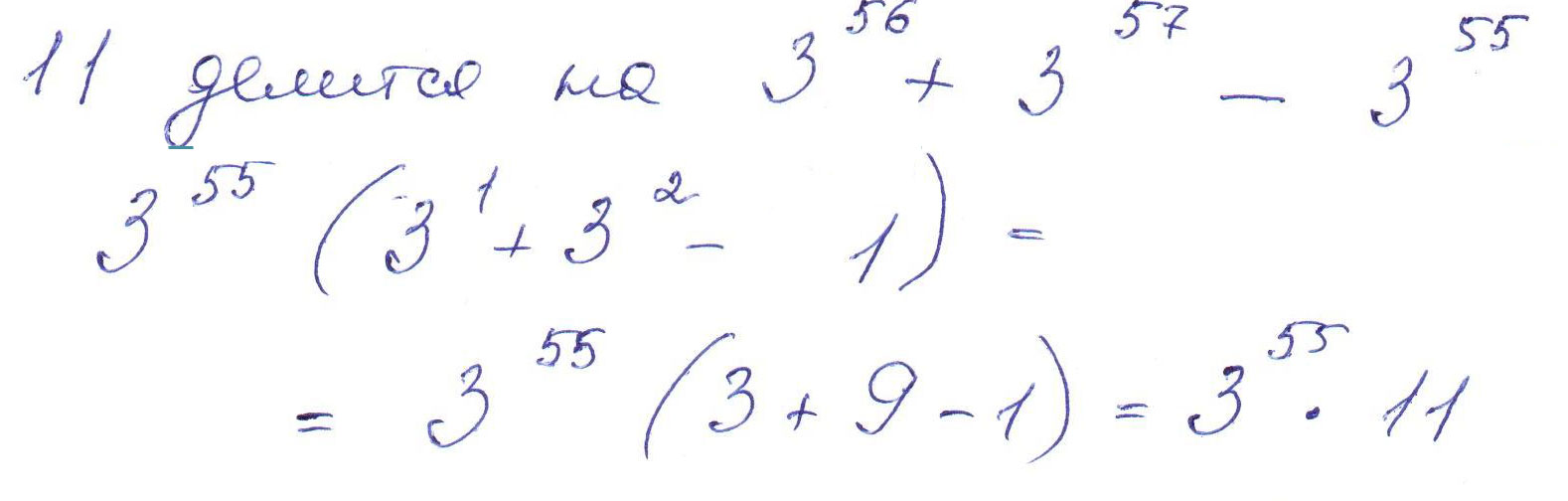степень умножить на степень

Как умножить число из под корня 3 степени на число из под корня 4 степени

Можно умножить только в том случае, если эти числа одинаковые, по правилу умножения степеней с одинаковыми основаниями, основание остается тем же, а показатели степеней складывают, например а^13 * a^1/4 = a^(1/3+1/4) = a^7/12; Если основания разные, то умножать можно в том случае, когда одинаковые показатели степеней, например: a^13 * b^1/3 = (ab)^1/3

a)798 ● 349 - 798 ● 249
б)57 ● 38 - 8640 : 24 + 66
в) 5^2+3^3.

а)8x+14=870 решите уравнения
б)5y-y=68

37k+13+22k упростите выражения
50×n×12

в двух корзинах 98 яблок в первой яблок в 6 раз меньше чем во второй сколько яблок в каждой корзине?

3)37к+13+22к=59к+13
4)6х+х=98 14*6=84
7х=98
х=14

Доказать что 11 делится на (3 степень 56) + (3 степень 57)- (3 степень 55) Вычислить : а) (5^6 умножить на 125 ) : 25 ^ 4 ; б) (3 ^ 6 умножить на 2 ^ 16) : 24 ^5

====================================   

а) (5^6*125 ) : 25 ^ 4

(5^6*5^3)/(5^2)^4

5^9/5^8=5

б) (3^6*2^16):24 ^5

(3^6*2^16)/(3^5*2^15)

3*2=6

Вычислите 2 в 10 степени умножить на 2 в 12 степени разделить на 2 в 21 степени

$$ 2^{10}*2^{12}:2^{21}=(2^{10}*2^{12}):2^{21}=\\= \frac{2^{10}*2^{12}}{2^{21}}= \frac{2^{10+12}}{2^{21}}= \frac{2^{22}}{2^{21}}= \frac{2^{1+21}}{1*2^{21}}= $$

$$ =\frac{2^1*2^{21}}{1*2^{21}}=\frac{2*2^{21}}{1*2^{21}}= \frac{2}{1} =2 $$

Икс в минус седьмой степени умножить на икс в девятой степени и всё это разделить на икс в четвертойстепени

Умножение чисел с одинаковыми основаниями, но разными по показателям степеней происходит так: основание остается прежним, а показатели степеней складываются, т.е. икс в минус седьмой умножить на икс в девятой степени будет равно иксу во второй степени (т.к. -7 + 9 = 2)
Деление чисел с одинаковыми основаниями, но разными показателями происходит подобным образом, только показатели степеней отнимаются, следовательно, икс во второй степени разделить на икс в четвертой степени будет равно иксу в минус 2 ( т. к. 2-4=-2)
Ответ: икс в минус второй степени