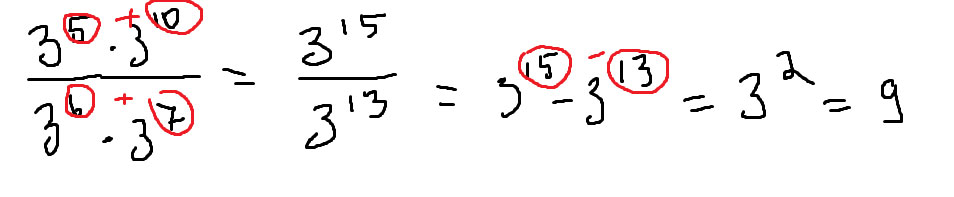степени »

степень умножить на степень - страница 2

  • В числителе 3 в 5 степени умножить на 3 в 10 степени в знаменателе 3 в 6 степени умножить на 3 в 7 степени


    Решение: , все подробно расписано

    3 в 5 степени* на 3 в 10 степени в знаменателе 3 в 6 степени *  на  3 в 7 степени= в числителе 9 в 15 степени а в знаменателе 9 в 13 степени= 9 во 2 степени

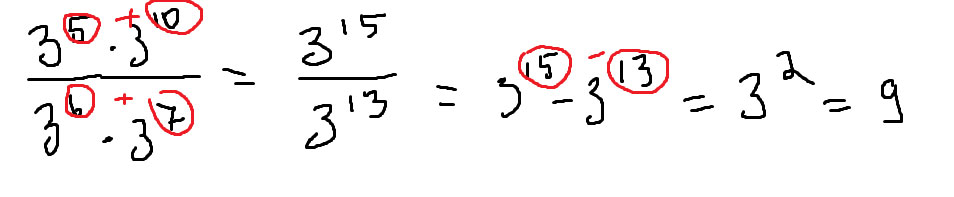
    все подробно расписано в степени на в степени в знаменателе в степени   на  в степени в числителе в степени а в знаменателе в степени во степени...

  • (2 в 8 степени)и в 3 степени умножить на 2 в 6 степени и все это делить на 2 в 22 степени --- (3 в 5 степени) и во 2 степени и все это делить на 3 в 6 степени умножить на 9 --- 4 в 7 степени умножить на 64 и все это делить на (4 в 4 степени) и в 3 степени ---


    Решение: 1) 2 в степени (8*3+6-22)= 2 в степени 8

    2) девять это 3 в степени 2, следовательно имеем 3 в степени(5*2/(6+2))=3 в степени два

    3) 64 это 4 в третьей, отсюда 4 в степени (7+3)/4*3=4 в степени (10/12)=> после сокращения дроби имеем 4 в степени 5/6, 4 это 2 во второй степени, отсюда

    => 2 в степени 10/6 снова сокращаем дробь получаем 2 в степени 5/3, иначе кубический корень из 2 в степени 5

  • Сколько различных делителей имеют числа 250,400 ? Указание:
    250=2*5(пять в третье степени); 400=2 в 4 степени умножить на 5 в 2 степени

    Придумайте, как определить количество различных делителей составного числа, пользуясь деревом выбора.


    Решение: Если число представлено как произведение степеней простых чисел, то количество делителей этого числа равно, произведению чисел, каждое из которых есть встречающаяся степень увеличенная на один
    $$ 250= 2*5^{3} $$, тогда 1+1+3+1 = 6 различных делителей
    $$ 400= 2^{4}*5^{2} $$, тогда 4+1+2+1 = 8 различных делителей 

  • Сколько различных делителей имеют числа 250,400 ?Указание:
    250=2*5(пять в третье степени); 400=2 в 4 степени умножить на 5 в 2 степени

    Придумайте, как определить количество различных делителей составного числа, пользуясь деревом выбора.
    Я только придумала 5 в 3 степени умножить на 2=250


    Решение: Если число представлено как произведение степеней простых чисел,то количество делителей этого числа равно,произведению чисел,каждое из которых есть встречающаяся степень увеличенная на один
    250 253,тогда 1+1+3+1=6 различных делителей
    400 2452, тогда 4+1+2+1=8 различных делителей

  • Дано числа а=2 в квадрате умножить на 3 в кубе умножить на 5 в 4-ой степени.б)2 в 5-ой степени умножить на 3 в кубе и умножить на 5 в квадрате с)2 в квадрате умножить на 3 в 5-ой степени и умножить на 5 в 4ой степени. НАЙТИ НОД(а,б,с) и НОК(а,б,с)


    Решение: А) 2 в квадрате * 3 в кубе * на 5 в 4-ой степени = 4 * 9 * 625 = 36 * 625 = 22500
    б) 2 в 5-ой степени * на 3 в кубе* на 5 в квадрате = 32 * 9 * 25 = 4950
    с)     2 в квадрате * на 3 в 5-ой степени *  на 5 в 4-ой степени = 4 * 81 * 625 = 202500

    А) НОД =1 ( это взаимно простые числа)
      НОК =5 * 5 * 5 * 5 * 2 * 2 * 3 * 3 = 625 * 36 = 17250
    Б) НОД = 1 ( это взаимно простые числа)
      НОК = 2 * 2 * 2 * 2* 2 * 5 * 5 * 3 * 3 = 32*25*9 = 7875
    С) НОД = 1 ( это взаимно простые числа)
      НОК = 5 * 5 * 5 * 5 * 3 * 3 * 3 * 3 * 2 * 2 = 625*81*4 = 122516

<< < 12 3 4 > >>