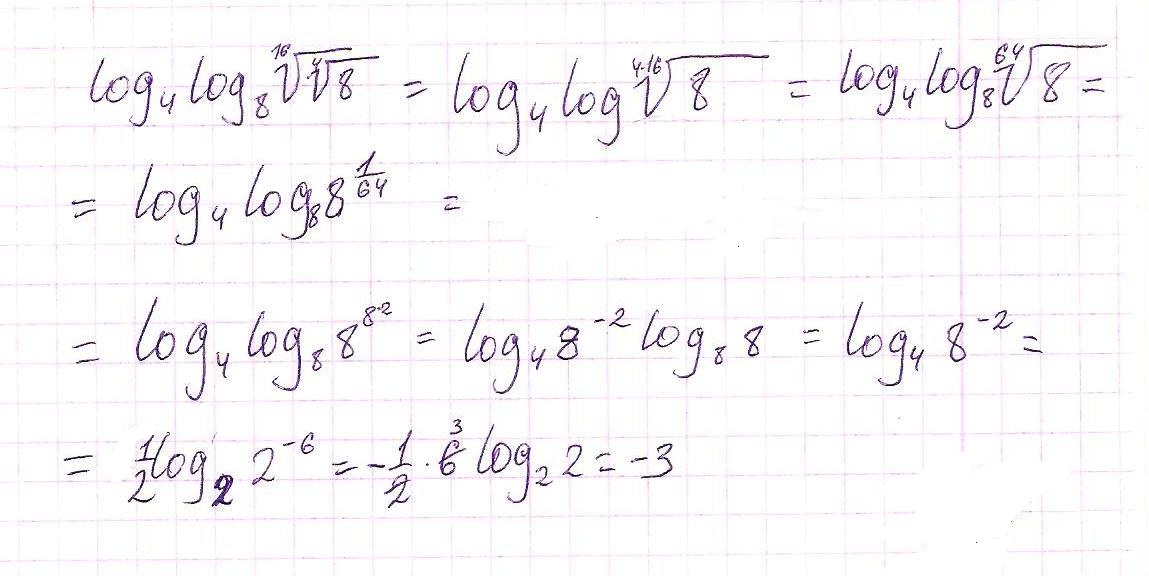корень n ой степени
Корень 3 степени из 1 (с мнимыми числами) (там, где должно быть 3 ответа, т.к. степень корня 3)
Решение:$$ \sqrt[3]{1}=?\\1=1+0i\\|1|= \sqrt{1^2+0^2}= \sqrt{1}=1\\(cos \alpha =1/|1|=1/1=1; $$ $$ sin \alpha = 0/|1|=0/1=0) = > \alpha =2\pi \\ \sqrt[3]{1}= \sqrt[3]{|1|}(cos \frac{ 2\pi+2\pi k }{3}+i sin\frac{ 2\pi +2\pi k }{3}) $$ $$ k=0,1,2\\ 1) k=0 \\ x_1=1(cos \frac{2\pi }{3}+isin \frac{2\pi }{3})=- \frac{\sqrt{3} }{2}+ \frac{1}{2}i $$
$$ 2) k=1\\ x_2=1(cos\frac{4\pi }{3}+isin(\frac{4\pi }{3}))=\\=- \frac{ \sqrt{3} }{2}- \frac{1}{2}i $$
$$ 2) k=2\\ x_2=1(cos \frac{6 \pi }{3}+isin( \frac{6 \pi }{3}))=\\=cos2 \pi +isin2\pi)=1+0i=1 $$
решить 7 класс... (0,001)^5*10^10/10^4
27^-2 * 9^2/3^-4
0,25^3*16^2/2^4
(корень 8 -4 корня из 3 + корень из 12)* корень из 2
(1-корень из 5)^2
корень 12 +3 корня из 6 /3 корня из 6
( корень 7 -1 )^2
корень 6 -3 корня из 2/3 корня из 2
где /- знаменатель ^ -степень
Решение: $$ \frac{(0,001)^5 *10^{10}}{10^4} = (10^{-3})^5 *10^{10}*10^{-4} = 10^{-15+10+(-4)}=10^{-9} $$
$$ \frac{27^{-2} *9^2}{3^{-4} }= (3^{3})^{-2} * (3^2)^2 *3^4 = 3^{-6 +4 +4} = 3^2=9 $$
$$ \frac{0.25^3 *16^2}{2^4} =(\frac{1}{4}) ^3 *( 2^4)^2 * 2^{-4} = ( 2^{-2})^3 * 2^8 *2^{-4} = 2^{-2} = \frac{1}{4} $$
(√8 - 4√3+√12)*√2= (2√2 -4√3 +2√3) *√2 = (2√2-2√3)*√2=
= 2√2 *√2 - 2√3*√2 = 2*2 -2√6 = 4-2√6
(1-√5)² = 1² -2*1*√5 + (√5)² = 1-2√5+5 =6-2√5
(√12 +3√6)/ 3√6 = (2√3+3√6) /3√6 =
=3√6(2√3 +3√6) / (3√6 *3√6) =
= (18√2 + 54) / 54 = 18(√2+3) / (18*3) =
= (√2+3)/3 = √2/3 +1
(√6-3√2 ) / 3√2 = 3√2(√6 -3√2) / (3√2 *3√2) =
= (6√3 -18)/18 = 6(√3-3)/ (6*3) = (√3-3)/3 = √3/3 -1
Вариант решения:$$ 1)\; \; \frac{(0,001)^5\cdot 10^{10}}{10^4}= \frac{10^{-15}\cdot 10^{10}}{10^4} =10^{-15+10-4}=10^{-9}\\3)\; \; \frac{0,25^3\cdot 16^2}{2^4}= \frac{2^{-6}\cdot 2^8}{2^4} =2^{-6+8-4}=2^{-2}=0,25\\2)\; \; \frac{27^{-2}\cdot 9^2}{3^{-4}}= \frac{3^{-6}\cdot 3^4}{3^{-4}} =3^{-6+4+4}=3^2=9\\4)\; \; (\sqrt8-4\sqrt3+\sqrt{12})\cdot \sqrt2=(2\sqrt2-4\sqrt3+2\sqrt3)\cdot \sqrt2=\\=2\cdot 2-2\sqrt3\cdot \sqrt2=4-2\sqrt6=2\sqrt2(\sqrt2-\sqrt3)\\5)\; \; (1-\sqrt5)^2=1-2\sqrt5+5=6-2\sqrt5=2(3-\sqrt5) $$
$$ 6)\; \; \frac{\sqrt{12}+3\sqrt6}{3\sqrt6}= \frac{\sqrt6(\sqrt2+3)}{3\sqrt6} = \frac{\sqrt2+3}{3} =1+\frac{\sqrt2}{3}\\7)\; \; (\sqrt7-1)^2=7-2\sqrt7+1=8-2\sqrt7=2\cdot (4-\sqrt7)\\8)\; \; \frac{\sqrt6-3\sqrt2}{3\sqrt2}= \frac{\sqrt6(1-\sqrt3)}{3\sqrt2} =\sqrt3\cdot (1-\sqrt3) $$
Решить log4log8из корень 16 степени из корня 4 степени 8
Решение: Решение в вложении. Первое что надо знать для решения этого задания, это то, что \sqrt[n]{x} = степень под корнем разделить на n.Второе - свойства логарифма (в вложении)
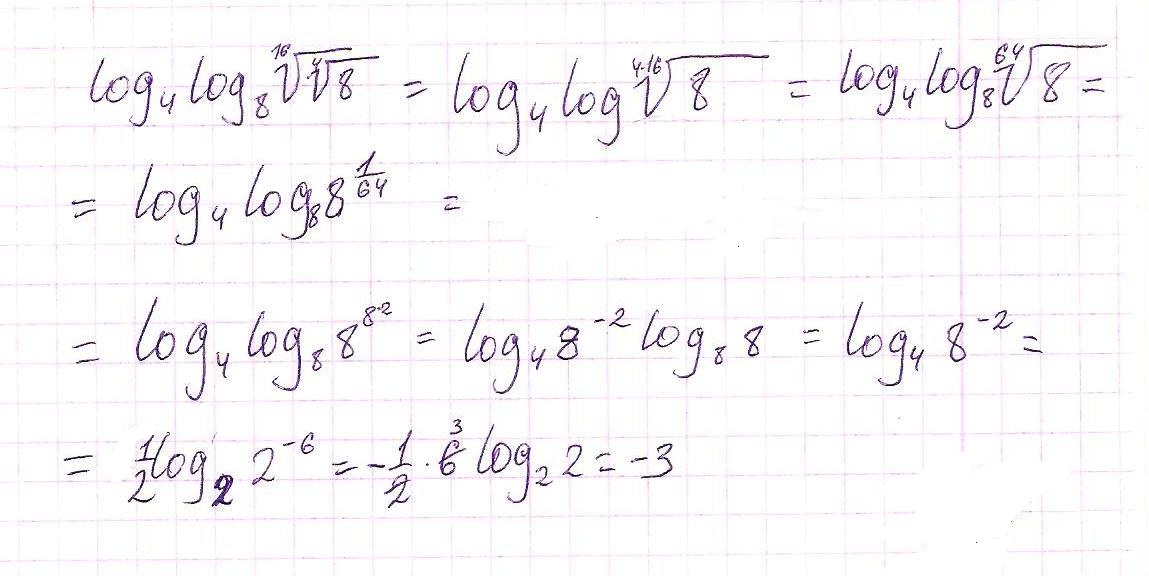
Решить уравнение 1) корень третьей степени из х - 2 корня шестой степени из х = 0 2) корень из х - 5 корней четвертой степени изх +6 = 0
Решение:1) корень третьей степени из х - 2 корня шестой степени из х = 0
Пусть,корень шестой степени из x=t, тогда уравнение принимает вид
t^2-2t=0
t*(t-2)=0
t1=0
t2=2
a) корень шестой степени из x =0 => x=0
б) корень шестой степени из x=2 => x=64
2) корень из х - 5 корней четвертой степени из х +6 = 0
Пусть корень четвертой степени из x=t, тогда
t^2-5t+6=0
D=b^2-4ac=1
t1=2
t2=3
a) корень четвертой степени из x=2 => x=16
б) корень четвертой степени из x =3 => x=81
Вынести из под корня (избавится от корня)
корень 3 степени из выражения 62*72*64
Решение: Вынести из под корня(избавится от корня)
корень 3 степени из выражения 62*72*64
(62*72*64)^(1/3)
62 = 2*31
72= 8*9 = 2^3*3^2
64 = 2^6
(62*72*64)^(1/3) = (2*31*2^3*3^2*2^6)^(1/3) = (2^9*2*9*31)^(1/3) =
=2^3(558)^(1/3)=8(558)^(1/3) = 8*8,233(приблизительно) = 65,864
Если использовать производную то получим
(62*72*64)^(1/3) = 8(558)^(1/3) =8(512+46)^(1/3)
f(x+дельта(x)) =f(x)+f’(x)*дельта(х)
x =512 =8^3
дельта(x) =46
f’(x) =(1/3)*(1/x^(2/3))
(512+46)^(1/3) = 512^(1/3) +(1/3)*(1/512^(2/3))*46 = 8+(1/3)(1/64)*46 =8+23/96=
(62*72*64)^(1/3) = 8(558)^(1/3) =8(8+23/96) =64+23/12 = 791/12 =65,92
Надо проверить условие, так как избавиться от корня не удастся с данными числами. Вынести из под корня можно 8. Это видно, если выражение под корнем разложить на множители:
62*72*64 = (31*2)*(8*9)*(8*8)
Тогда:
корень 3 степени из выражения 62*72*64 = 8*кор.3 степ из 558