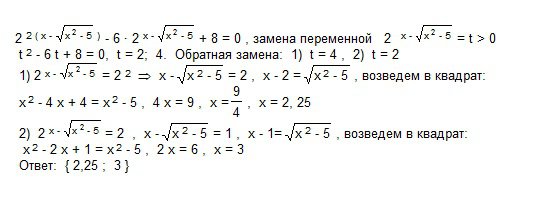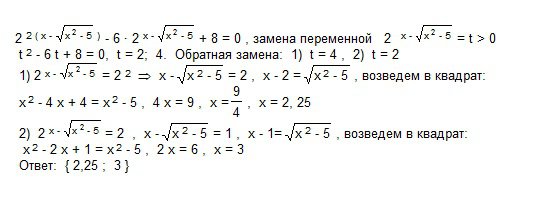степени »

корень n ой степени - страница 2

  • Решите уравнение. Степень 3 открывается корень.под корнем : х в 3 степени - х во второй степени + 1 (корень закрылся)= степень 3 корень открывается 2х в квадрате - 2х +1


    Решение: $$ \sqrt[3]{ x^{3}- x^{2} +1} =\\= \sqrt[3]{2 x^{2}-2x+1} $$ /возводим обе части в куб

    $$ (\sqrt[3]{ x^{3}- x^{2} +1})^{3} = ( \sqrt[3]{2 x^{2}-2x+1} )^{3} $$

    х³ - х² + 1 = 2х² - 2х +1
    х³ - 3х² + 2х = 0
    х(х² - 3х + 2) = 0
    (х² - 3х + 2) = 0 или х₁ = 0
    а = 1; b = -3; c = 2
    D = b² - 4ac = (-3)² - 4 * 1 * 2 = 9 - 8 = 1

    x    ₂ = - b + √D   = - ( - 3) + √1   =  3 +  1   = 2
       2a 2 * 1   2

    x    ₃ = - b - √D   =  - ( - 3) - √1   =  3 -  1  = 1
       2a 2 * 1   2

    Ответ: 0; 1; 2

  • 1) Объем правильной треугольной пирамиды равен 3 корня из 3 смкуб. Радиус окружности ,описанной около основания пирамиды равен 2 корня из 3/3 см. Найдите высоту пирамиды.
    2)А)корень 4 степени х+1 +20(без корня) = корень х+1
    Б)(х в квадрате -4)(корень и 6 - 5х -х(без корня)=0


    Решение: 1
    V=1/3*1/2*a²√3/2*h=a²h√3/12
    a=R√3=2√3/3*√3=2см
    4h√3/12=3√3
    √3h/3=3√3
    h=3√3:√3/3=3√3*3/√3=9
    2
    a)ОДЗ x∈[-1;∞)
    корень 4 степени х+1=a
    a    ²-a-20=0
    a1+a2=1 U a1*a2=-20
    a1=-4⇒корень 4 степени х+1=-4 нет решения
    a2=5    ⇒корень 4 степени х+1=5
    x+1=625
    x=624
    б)ОДЗ
    6-5x    ≥0⇒x≤1,2
    х²-4=0
    х²=4
    х=-2
    х=2 не удов усл
    √(6-5x)-x=0
    √(6-5x)=x
    x≥0
    6-5x=x²
    x²+5x-6=0
    x1+x2=-5 U x18x2=-6
    x1=-6 не удов усл
    x2=1
    Ответ x=1;x=-2

  • 1.(16\81)^1\4+5^0=
    2. (корень степени 5 в корне 9*8)*(корень степени 5 в корне 27*4)=
    3. 4 sin 30 градусов + 6 cos 60 градусов - 2 tg 45 градусов=


    Решение:

    1) $$ ( \frac{16}{81} ) ^{ \frac{1}{4} } +5^0= \sqrt[4]{ (\frac{2}{3} )^{4} } +1= \frac{2}{3} +1=1 \frac{2}{3} $$

    2) $$ \sqrt[5]{9*8} * \sqrt[5]{27*4} = \sqrt[5]{3^2*2^3*3^3*2^2} = \sqrt[5]{3^5*2^5} =3*2=6 $$

    3) $$ 4sin30+6cos60-2tg45=4* \frac{1}{2} +6* \frac{1}{2} -2*1=2+3-2=3 $$

    $$ 1)( \frac{16}{81} ) ^{ \frac{1}{4} } +5 ^{0} = \frac{2}{3} +1=1 \frac{2}{3} \\ \ 2) (\sqrt[5]{9*8} )* \sqrt[5]{27*4} = \sqrt[5]{3 ^{2}*2 ^{3} *3 ^{3} *2 ^{2} } = \sqrt[5]{3 ^{5} *2 ^{5} } =3*2=6 \\ \ 3)4sin30+6cos60-2tg45=4* \frac{1}{2} +6* \frac{1}{2} -2*1=2+3-2=3 $$

  • Как упростить? \( \frac {5\sqrt[3]5}{\sqrt[4]{5\sqrt[3]5}} \) 5 корней третьей степени из 5 деленное на корень 4-ой степени из 5 корней третьей степени из пяти


    Решение: (5*5^1/3) / (5^1/4 *(5^1/3)^1/4)  =  (5*5^1/3) / (5^1/4 * 5^1/12)  =  (5*5^1/3) / 5^(1/4 + 1/12)  =

    =(5*5^1/3) / 5^1/3  =  5

    Ответ.5

  • 4в степени х-корень х в квадрате -5 дальше 12*2 в степени х-1-корень х в квадрате -5 дальше +8=0


    Решение: После (-5), видимо, надо написать " - ". Тогда все получается, если использовать способы решения показательных уравнений и иррациональных уравнений. И еще надо найти ОДЗ и проверить по ней полученные корни, или проверить их просто подстановкой в исходное уравнение

    После - видимо надо написать - . Тогда все получается если использовать способы решения показательных уравнений и иррациональных уравнений. И еще надо найти ОДЗ и проверить п...
<< < 12 3 4 > >>