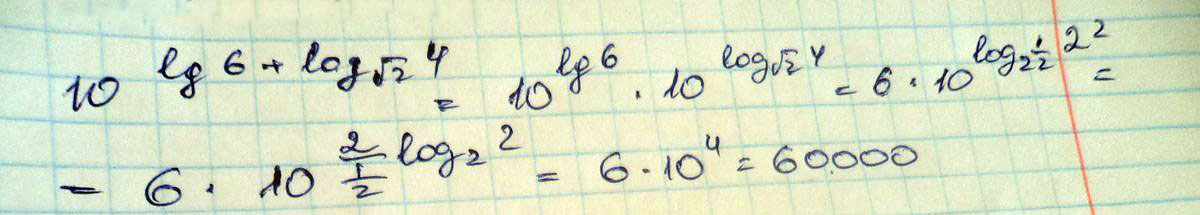степени »
степень логарифма
Логарифм по основанию 3 логорифма по основанию 9 корень 27 степени, а под корнем корень кубический из9
Решение: log log √∛9=
осн-е3 осн-у9 корень 27
степени
Надо начинать с внутреннего логарифма. Корень будет 81 степени( 27·9), показатель у девятки будет 1/81, показатель выносится за знак логарифма, под логарифмом остаётся 9 и этот логарифм =1
Под внешним логарифмом остаётся 1/81
log 1/81 = - 6
осн-е 3Тут десятичный логарифм 6+ log в корне из двух в степени 4. Как решить и каков ответ?
Решение: Чтобы десятичный логарифм не смущал, пиши его всегда как обычный с основанием 10. Сразу увидите основное логарифмическое тождество)
$$ 10 ^{log _{10}6+ log_{2} 2 }= 6*10=60 $$
Логарифм по осн. корень из 2 выражения 4 преобразовал: степень 1/2 перенёс в выражение и получил логарифм двух по основанию 2.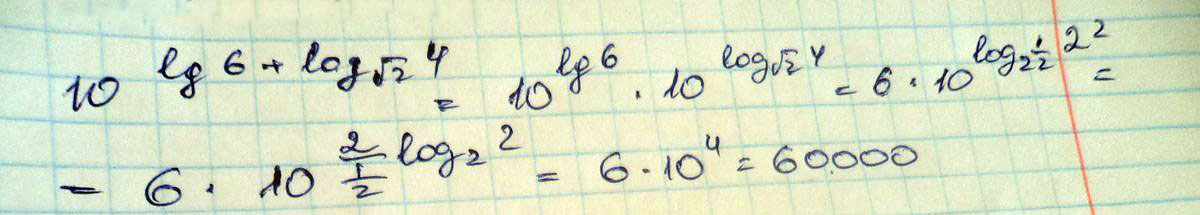
Степени и логарифмы: \( \frac{(2^ \frac{11}{15} \cdot 9^\frac{3}{5})^{15}}{18^9} \)
Решение: 11. 4
$$ \frac{(2^ \frac{11}{15} \cdot 9^\frac{3}{5})^{15}}{18^9}=\frac{2^{\frac{11}{15} \cdot 15} \cdot 9^{\frac{3}{5} \cdot 15}}{2^9 \cdot 9^9}=\frac{2^{11} \cdot 9^{9}}{2^9 \cdot 9^9}=2^2=4 $$
12. 32
$$ 64^{0,5} \cdot2^2=\sqrt{64} \cdot 4=8 \cdot 4=32 $$
13. 90
$$ \frac{3^ \frac{18}{7} \cdot 10^\frac{11}{7}}{30^\frac{4}{7}}=\frac{3^ \frac{18}{7} \cdot 10^\frac{11}{7}}{3^ \frac{4}{7} \cdot 10^\frac{4}{7}}=3^\frac{14}{7} \cdot 10^\frac{7}{7}=3^2 \cdot 10=9 \cdot 10=90 $$
14. 21
$$ 3 \cdot 2^{log_27}=3 \cdot 7=21 $$
15. 27
$$ \frac{3^{9,66}}{27^{2,22}} =\frac{3^{9,66}}{(3^3)^{2,22}} =\frac{3^{9,66}}{3^{6,66}}=3^3=27 $$
Степени и логарифмы: найдите значение выражения \( \frac{225\frac{3}{5}}{15\frac{1}{5}} \); \( \frac{9\frac{22}{7}4\frac{1}{7}}{36\frac{1}{7}} \); \( \frac{20\frac{8}{5}}{4\frac{3}{5}5\frac{8}{5}} \);
\( 2log_4 8 - 3log_8 4 +log_2 32 +18 \); \( log_4 8 +log_4 2 \); \( log_4 32b, \;\;\;если\;\;\;log_2 b=3 \)
Решение: Ответы:
№1: 15
№2: 729
№3: 1 (если там везде степени 8/5. очень плохо видно в знаменателе степень числа 4. Если в знаменателе, там где 4 степень 9/5, то ответ будет 4^ -1/5)
№4: 24
№5: 2
№6: 4
Пояснение задания №1.
Числитель 225^3/5. 225(пока без учета степени) представляем как 15^2. Полученную степень 2 перемножаем со степенью 3/5. Получаем 6/5. По свойству степеней, так как выполняется деление, то степени с одинаковым основанием вычитаются: 15 ^ 6/5 : 15 ^ 1/5 = 15 ^ 5/5 =15.
Пояснение задачи №2:
Знаменатель 36^1/7. Раскладываем это число как 9^1/7 x 4^1/7. Получаем одинаковые основания и в числителе, и в знаменателе. Вычитаем степени и получаем результат.
Пояснение задачи №4.
Тут нужно знать свойства логарифмов.
Самое основной свойство логарифмов, связанное со степенями:
Пример: $$ Log_{4}8 $$
И число, и основание в данном случае, нужно сделать так, чтобы и то и другое было равно друг другу, чтобы в результате получить равное единице: $$ Log_{a} a =1 $$. Так 4 можно представить как 2^2, а 8 как 2^3. Привели. Дальше надо усвоить, что степени можно вынести за логарифм, при чем степень числа будет являться числителем коэффициента, а основание - знаменателем. Т.е, в данном примере получится коэффициент 3/2 и пример будет выглядеть таким образом: 3/2 $$ Log_{2}2 $$.
Пояснение задачи №6.
Тут действуют формулы:
$$ Log_{a} X*Y = Log_{a}X + Log_{a} Y $$
$$ Log_{a} X/Y = Log_{a}X - Log_{a} Y $$
В данном случае мы берем формулу 1, где сложение и умножение. Из умножения мы разбиваем каждый логарифм, выполняя сложение. И дальше опять приводим основание и число к одному, вынося степени как коэффициент.
*Прочие формулы:
$$ Log_{a} b = \frac{1}{ log_{b}a} $$
$$ a^{ log_{a}b} =b $$
Решить логарифм такого вида:
(3^2log3 6) (3 степень 2log шести по основанию три)
Решение: Это решается по основному логарифмическому тождеству. Сначала преобразуй степень.
Двойку от логарифма перенеси в степень к шестёрке. Получится лог 36 по основанию 3
А теперь по основному тождеству: основание лога совпадает с основанием степени. Поэтому ответом является логарифмируемое число.