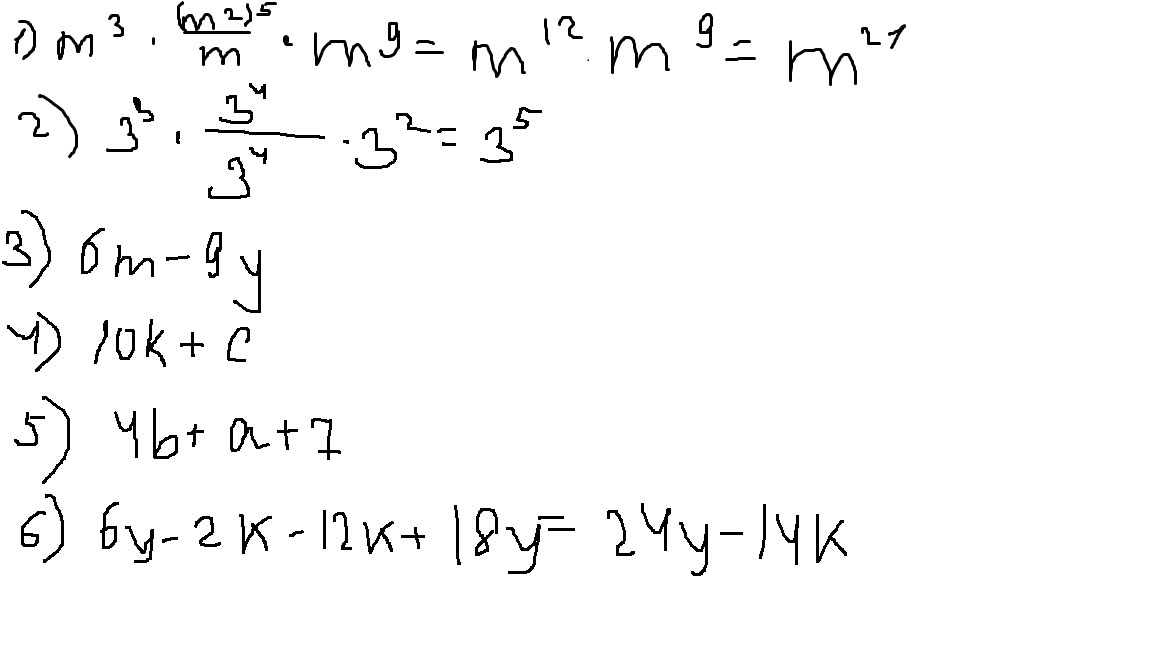действия с степенями - страница 4

Действия со степенями, решить уравнения: \( 2^{x+1}+3\cdot 2^{x-1} -4\cdot 2^x =0 \\ 7^{x-1}=343 \\ 36^x-5\cdot 6^x=6 \\ 4^x =7^x \)

Выполнить действия со степенями, 1)n^3/4+3(n^1/4)^3
2) 3*36^1/2*125^1/3-20*256^1/4
3)(1/8n^3/2)^-1/3?, при n=4
4)18^2p:36^p, при p=2

Действия со степенями :
а)m^3 * (m^2)^5/m * m^9
б)27 * 9^2/3^4 * 3^2
2)выполните действия :
а)m-3y +5m-6y
б)(7k-3c)+(3k+4c)
в)(7b-3a-2) - (3b-4a-9)
г)(6y-2 * k-6 * (2k-3y))

г)(6y- .....................................................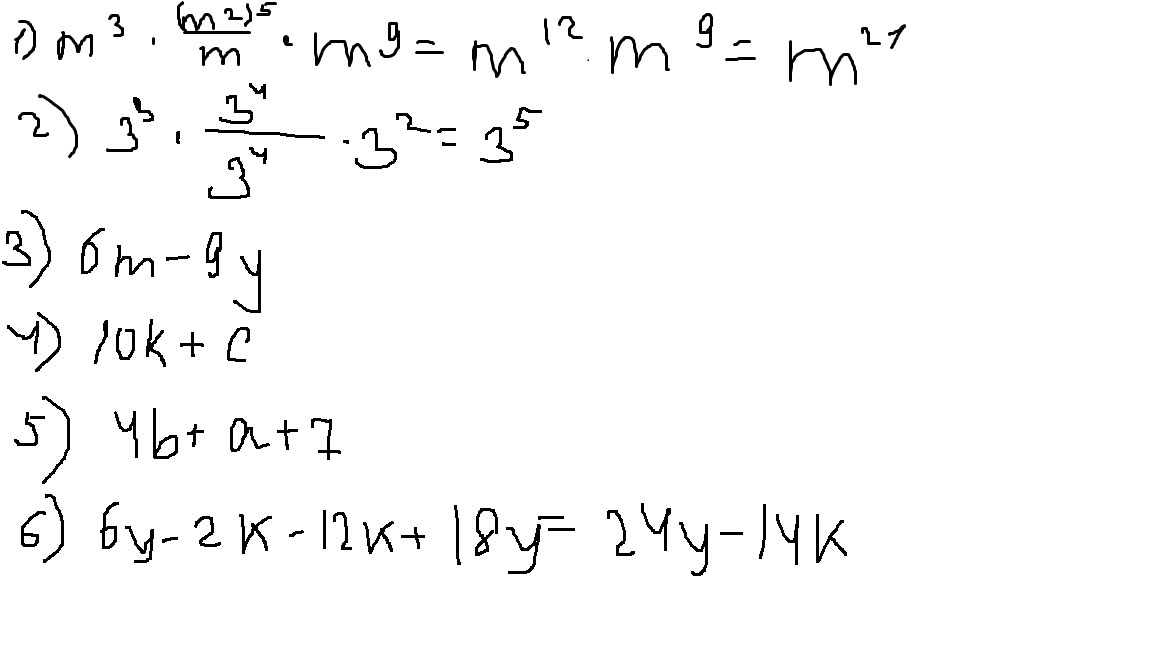

Действия со степенями с рациональным показателем: 1. Представьте в виде степени с рациональным показателем: \( a^{\frac{2}{5}}b^{-\frac{3}{4}}c^{\frac{1}{2}}\cdot a^{-\frac{3}{5}}b^{\frac{1}{2}}c^{-\frac{1}{3}} \)
2. Найдите значение выражения: \( \left ( \frac{a^{-\frac{3}{5}}b^{-\frac{3}{5}}\cdot \sqrt[5]{b^{-3}}}{(ac)^{-\frac{4}{5}}b^{-\frac{7}{5}}}+9bc\right )^{-3}= \) при a=32; b=c=1/3

$$ 1) a^{\frac{2}{5}}b^{-\frac{3}{4}}c^{\frac{1}{2}}\cdot a^{-\frac{3}{5}}b^{\frac{1}{2}}c^{-\frac{1}{3}}=a^{\frac{2}{5}-\frac{3}{5}}\cdot b^{-\frac{3}{4}+\frac{1}{2}} \cdot c^{\frac{1}{2}-\frac{1}{3}}=\\=a^{-\frac{1}{5}}\cdot b^{-\frac{1}{4}}\cdot c^{\frac{1}{6}}=\frac{c^{\frac{1}{6}}}{a^{\frac{1}{5}}\cdot b^{\frac{1}{4}}}=\frac{\sqrt[6]{c}}{\sqrt[5]{a}\sqrt[4]{b}}\\2)\; \; a=32,b=c=\frac{1}{3}\\\left ( \frac{a^{-\frac{3}{5}}b^{-\frac{3}{5}}\cdot \sqrt[5]{b^{-3}}}{(ac)^{-\frac{4}{5}}b^{-\frac{7}{5}}}+9bc\right )^{-3}= $$

$$ =\left (\frac{a^{-\frac{3}{5}}b^{-\frac{6}{5}}}{a^{-\frac{4}{5}}c^{-\frac{4}{5}}b^{-\frac{7}{5}}}+9bc\right )^{-3}=\left (a^{\frac{1}{5}}b^{\frac{1}{5}}c^{\frac{4}{5}}+9bc)\right )^{-3}=\\=\left (\sqrt[5]{32\cdot \frac{1}{3}\cdot \frac{1}{3^4}}+9\cdot \frac{1}{3}\cdot \frac{1}{3}\right )^{-3}=\left (\sqrt[5]{2^5\cdot \frac{1}{3^5}}+9\cdot \frac{1}{3^2}\right )^{-3}=\\=\left (\frac{2}{3}+1\right )^{-3}=(\frac{5}{3})^{-3}=\frac{27}{125} $$

Тема "Действия со степенями с рациональным показателем "