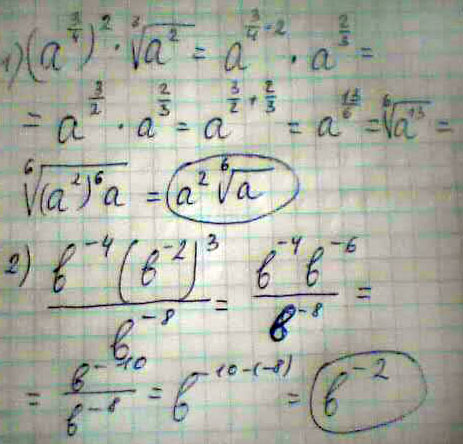степени »

представьте выражение в виде степени с основанием - страница 3

  • Представьте выражение в виде степени


    Решение:

    $$ \frac{25^7\cdot15^2}{9\cdot 125^5}=\frac{(5^2)^7\cdot(3\cdot5)^2}{3^2\cdot(5^3)^5}=\\=\frac{5^14\cdot3^2\cdot5^2}{3^2\cdot5^15}=\frac{5^16}{5^15}=5^1=5 $$

    $$ \frac{(9^2)^8\cdot (2^7)^2\cdot 3^2}{(3^2)^15\cdot 2\cdot 8^3}=\frac{(3^2)^16\cdot 2^14\cdot 3^2}{3^30\cdot 2\cdot (2^3)^3} =\\= \frac{3^32\cdot 2^14\cdot 3^2}{3^30\cdot 2\cdot 2^9 } = \frac{3^34\cdot 2^14}{3^30\cdot 2^10 } = 3^4\cdot2^4=6^4 $$

  • Представьте выражение в виде степени и найдите его значение при заданном значении переменной
    3A.18
    a) a^-9/(a^2)^-3; a=1/2; б)(m^6)^-2*m^-14;m=1/4
    3А.19
    а)1/x^-9:x^3;x=0.1: б)а^3:1/a^-5;a=0.1
    3A.20
    a)(c^3*c^-3)^-1;c=1/3; б)a^7*(a^-5)^2;a=1/5
    3A.21
    a)1/x^-1*1/x^-4;x=-2; б)1/a^-2*1/2^-4;a=2
    3A.22
    a)(a^2)^3/a^8;a=2/4 б)x^9/(x^3)^4;x=2/3
    3A.23
    a)a^-9/a^-2*a^-5;a=1/2 б)a^-6/a^-3*A^-2;a=2/3


    Решение:

    3A.18
    a) a^(-9)/(a^2)^(-3)=a^(-9)/a^(-6)=a^(-9+6)=a^(-3)=1/a^3
    при a=1/2 получим  1/(1/8)=8;
    б)(m^(-6))^(-2)*m^(-14)=m^(12)*m^(-14)=m^(12-14)=m^(-2)=1/m^2
    при m=1/4 получим 1/(16)=16
    3А.19
    а)1/x^(-9):x^3=х^9:x^3=x^6
    при x=0.1 получим 0,000001
     б)а^(-3):1/a^(-5)=a^(-3)*a^5=a^2
    при a=0.1 получим 0,01
    3A.20
    a)(c^3*c^(-3))^(-1)=(с^(3-3))^(-1)=(c^0)^(-1)=1^(-1)=1
    при c=1/3  получим 1;
     б)a^7*(a^(-5))^2=a^7*a^(-10)=a^(7-10)=a^(-3)=1/a^3
    при  a=1/5  получим  1/(1/125)=125
    3A.21
    a)(1/x^(-1))*(1/x^(-4))=х*х^4=x^5
    при x=-2 получим (-2)^5=-32
     б)(1/a^(-2))*(1/a^(-4))=a^2*a^4=a^6
    при a=2  получим 2^6=64
    3A.22
    a)(a^2)^3/a^8=a^6/a^8=a^(-2)=1/a^2
    при a=3/4  получим  1/(9/16)=16/9
    б)x^9/(x^3)^4=x^9/x^12=x^(9-12)=x^(-3)
    при x=2/3  получим
    (2/3)^(-3)=27/8
    3A.23
    a)a^-9/a^-2*a^-5=a^(-9)/a^(-7)=a^(-9+7)=a^(-2)
    при a=1/2 получим 4
    б)a^-6/a^-3*a^-2=a^(-6)/a^(-3-2)=a^(-6)/a^(-5)=a^(-1)
    при  a=2/3  получим 3/2=1.5

  • N151.(а,б,в)Представьте,если возможно,выражение в виде степени: А)-yв 3 степени умножить (-y)в 5 степени .Б)b в 6 степени умножить (b) в 10 степени. иВ)(a-b) в 3 степени за скобками умножить (b-a) в 2 степени за скобками. решить


    Решение:

    А)-yв 3 степени умножить (-y)в 5 степени = (-у)^8

    Б)b в 6 степени умножить (b) в 10 степени=b^16

    В)(a-b) в 3 степени за скобками умножить (b-a) в 2 степени за скобками. 

    так как b-a и а-b равны и отличаются только знаком "-", но при возведении в квадрат любое число становится положительным, то вместо (b-a)^2 записываем (a-b)^2

    (a-b)^3*(b-a)^2=(a-b)^3*(a-b)^2=(a-b)^5

      

  • 1) Выполните действия (a¾)² ³√a² 2)Представьте выражение в виде степени b⁻⁴ (b⁻² )³ /b ⁻ ⁸


    Решение:

    1)1)Выполните действия 

    a¹³/⁶

    2)Представьте выражение в виде степени

    b ⁻²

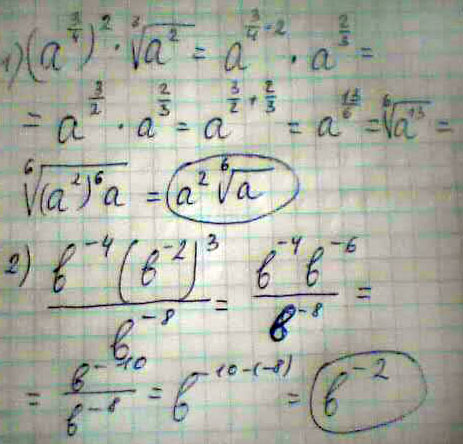
    Выполните действия  a Представьте выражение в виде степени b ...

  • Представьте в виде степени с основанием 2 выражение:1) 8^9х4^5
    2) 32х16^6х64^3


    Решение: $$ 8^{9} * 4^{5} = 2^{27} * 2^{10} = 2^{37} \\ \ 32* 16^{6} * 64^{3} = 2^{5} * 2^{24}* 2^{18} = 2^{47} $$

    1) 8^9х4^5 = 2¹²x2⁷=2¹⁹ (степени с одинаковыми основаниями - складываются)
    8 - это 2, умноженная на себя три раза, то есть в степени 9+3=12, то есть 2 в 12 степени.
    4 - это 2, умноженная на себя 2 раза, то есть в степени будет 5+2=7, то есть 2 в 7 степени
    Аналогично:
    2) 32х16^6х64^3 = 2⁵x2²⁴x2¹⁸=2⁴⁷

<< < 123 4 > >>