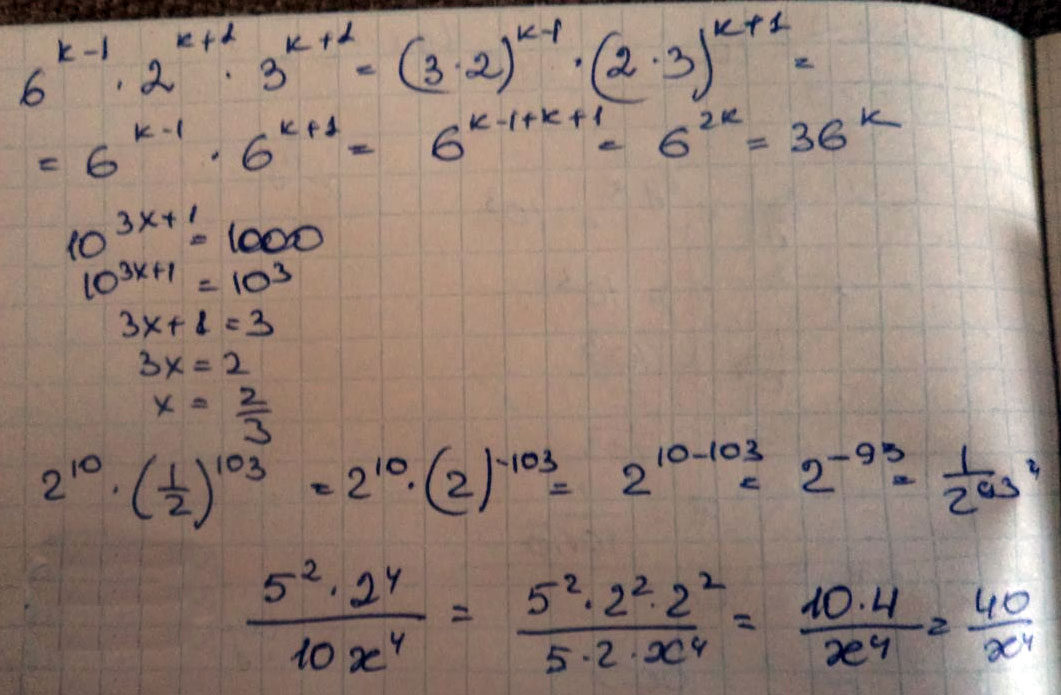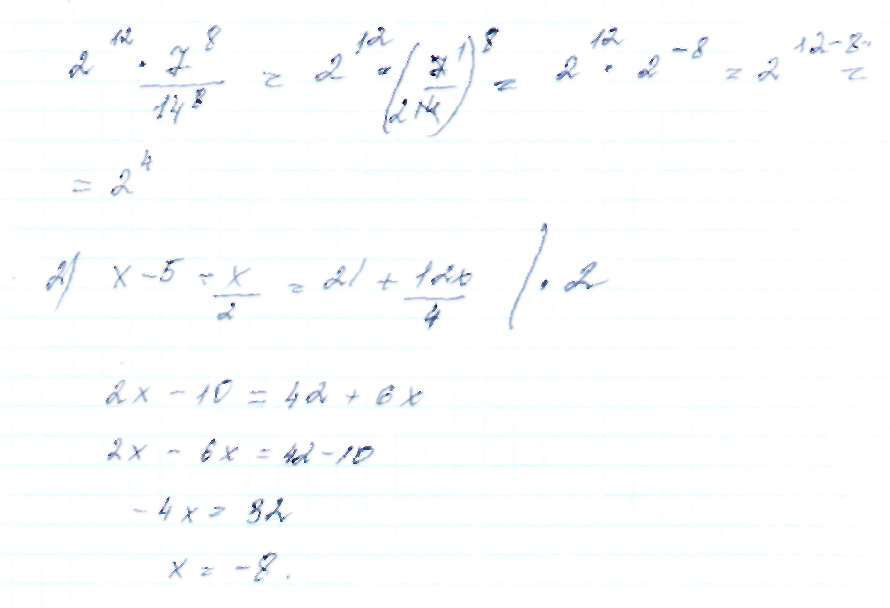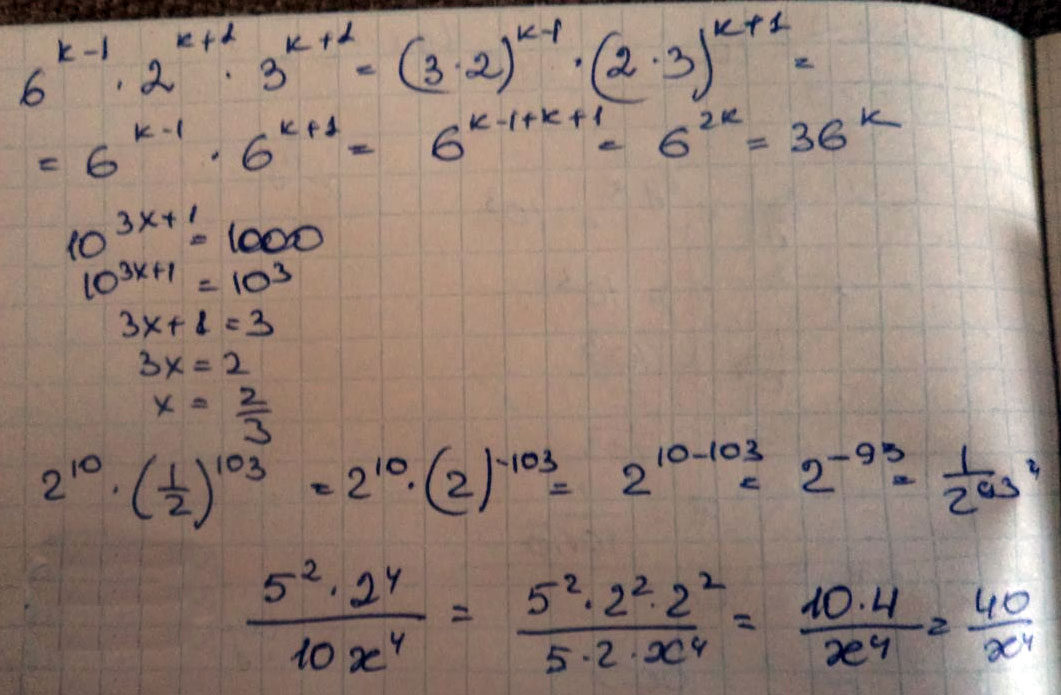степени »

представьте выражение в виде степени с основанием - страница 4

  • Представьте выражение \( \frac{ x^{-6} }{ x^{-3} x^{-2} } \) в виде степени и найдите его значение при \( x=\frac{2}{3} \)


    Решение: В знаменателе при умножении х в минус третьей степени на х в минус второй степени получится х в минус пятой степени 
    а при делении х в минус шестой степени на х в пятой степени получится х в минус первой степени 
    и так как х равен две третьих, значит ответ будет минус две третьих 

  • Представьте в виде степени выражения: а) \( x^{3} * x^{5} *x^{0} *x \)
    б) \( x^{18} : x^{6} \)
    в)\( x^{50} : x^{50} \)
    г) \( x^{10} : x^{0} \)
    д) \( \frac{x^8 x^4}{x^6 x^5} \)
    е) \( (x^{3} )^4 \)
    ж) \( (x^{2} )^m \)


    Решение: А) х^9
    б) х^3
    в) х^1
    г) x^10
    д) x^1
    е) x^12
    ж) x^2m

    $$ 1) x^{3} * x^{5} * x^{0} * x= x^{3+5+1} = x^{9} \\ 2) \frac{ x^{18} }{ x^{6} } = x^{12} \\ 3) \frac{ x^{50} }{ x^{50} } =1 \\ 4) \frac{ x^{10} }{ x^{0} } = \frac{ x^{10} }{1} = x^{10} \\ 5) \frac{ x^{8} * x^{4} }{ x^{6} * x^{5} } = \frac{ x^{8+4} }{ x^{6+5} } = \frac{ x^{8+4} }{ x^{6+5} } = \frac{ x^{12} }{ x^{11} } = x^{12-11} = x^{1} =x \\ 6) (x^{3} ) x^{4} = x^{3*4} = x^{12} \\ 7)( x^{2} ) ^{m} = x^{2m} $$

  • представьте выражение в виде степени с основанием х:
    \( \frac{x^{-7}}{x^{10} \cdot x^{-2}} \)


    Решение:

    -7-(10-2)=-15

    x^(-15)

    --------------------------------------

    число с отрицательной степенью ставиться в знаменатель и возводиться положительной степенью то есть х в -7 уйдет вниз и будет х в7...а х в -2 уйдет вверх и будет х в 2...тогда в числителе будет х во 2 а знаменателе х в 10 и х в 7 и тогда результатом выражения будет 1/х в 15 или х в -15

  • 1. Представьте выражение 2^12*7^8/14^8 в виде степени с основанием 4. 2. Решите уравнение x-5-x/2=21+12x/4.


    Решение: 1)$$ 2^{12}*7^{8}/2^{8}*7^{8}=2^{4}=4^{2} $$

    2)$$ \frac{ 2x-10-x}{2}=21+3x|*2 $$

    x-10=42+6x

    -5x=32

    x=-6,4

    решение во вложении

    frac x- -x x x- x - x x - решение во вложении...

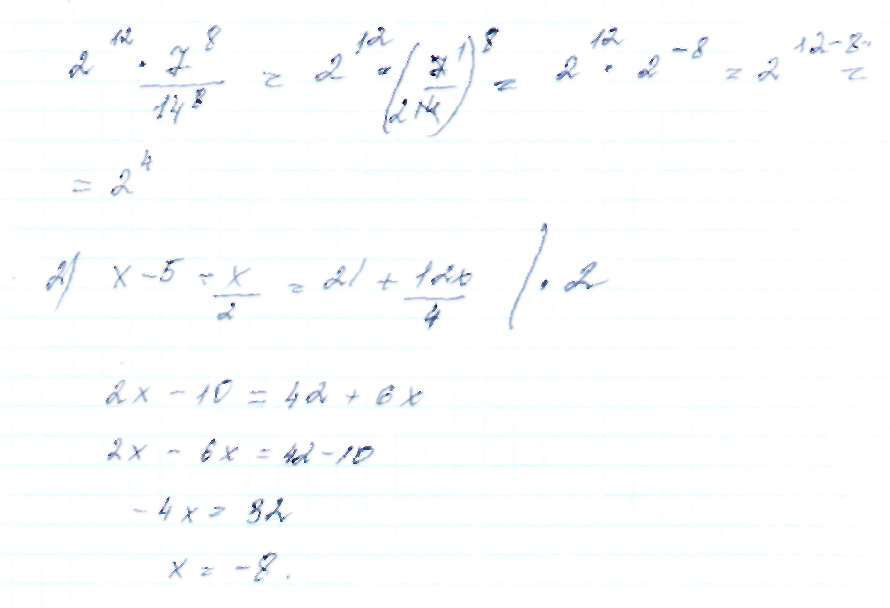
  • Степени. Представьте в виде степени: \( 6^{k-1} 2^{k+1} 3^{k+1} \)
    При каких значениях х выполняется равенство:\( 10^{3x+1} =1000\)
    Вычислите: \( 2^{10} * ( \frac{1}{2})^{103} \)
    Найдите значение выражения: \( \frac{5^{2} * 2^{4} }{10 x^{4}} \)


    Решение: $$ 1) \\ 6^{k-1}2^{k+1}3^{k+1} = 6^{k-1}2^{k+1}3^{k+1} = 6^{k-1}(2*3)^{k+1} =\\ 6^{k-1}6^{k+1} = 6^{k -1 + k + 1} = 6^{2k} = \boxed{36^k}\\ 2) \\ 10^{3x+1} = 1000\\ 10^{3x+1} = 10^3\\ 3x + 1 = 3, \\ 3x = 2, \\ \boxed{x = \frac{2}{3}}\\ 3) \\ 2^{100}*(\frac{1}{2})^{103} = 2^{100}*2^{-103} = 2^{-3} = \boxed{\frac{1}{8}}\\\ 4) \\ \frac{5^2*2^4}{10^4} = \frac{5^2*2^4}{(2*5)^4} = \frac{5^2*2^4}{2^4*5^4} = \frac{5^2}{5^4} = 5^{-2} = \boxed{\frac{1}{25}} $$ k- k k k- k k k- k k- k k - k k boxed k x x x x boxed x frac frac - - boxed frac frac frac frac frac - boxed frac...
<< < 234