найдите значение дроби
Зная, что m принадлежит z, найдите целые значения дроби: m^2-10m+27/m-5
Решение: (m²-10m+27)/(m-5)=(m²-10m+25)/(m-5)+2/(m-5)=(m-5) +2/(m-5)
m=3 -2-1=-3
m=4 -1-2=-3
m=6 1+2=3
m=7 2+1=3
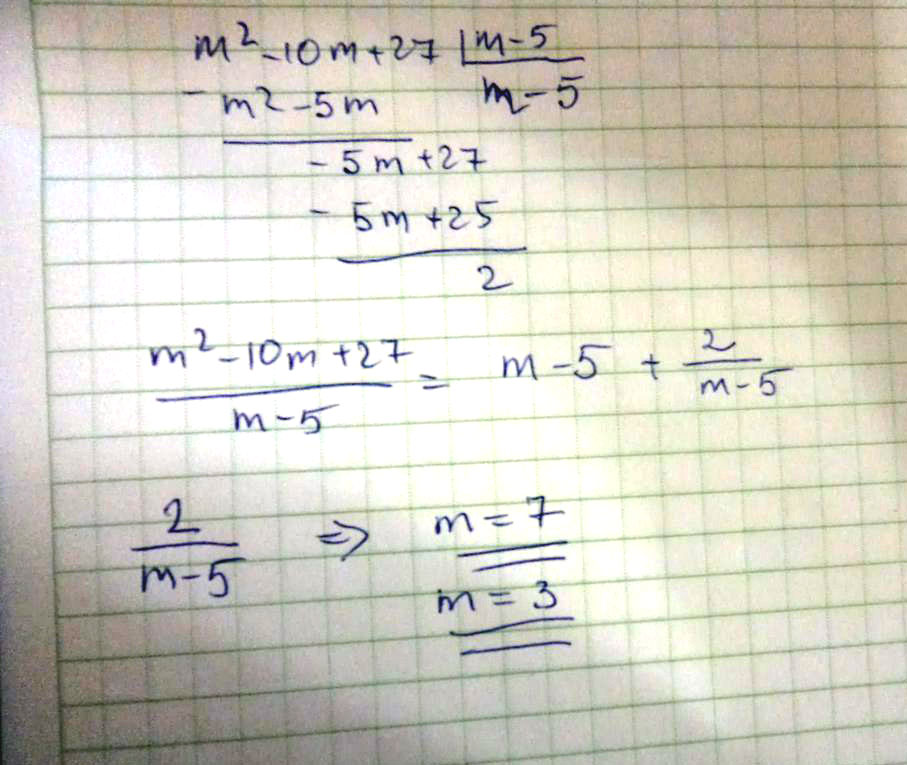
Найдите все целые значения дроби (n^2-4)/(n+3), зная, что n принадлежит N.
Решение: $$ \frac{n^2-4}{n+3}=\\= \frac{n^2-9+5}{n+3}=\\= \frac{(n-3)(n+3)+5}{n+3}=\\= n-3+\frac{5}{n+3}\\ n\in\mathbb{N}\wedge n+3ot=0 \wedge n+3\leq5 \wedge (n+3)|5\\ n\in\mathbb{N}\wedge not=-3 \wedge n\leq2 \wedge (n+3)|5 \Rightarrow n=2\\ 2-3+\frac{5}{2+3}=\\= -1+1=\ 0 $$Дробь: (n²-4)/(n+3). ОДЗ: х≠-3.
Данная дробь имеет целое значение тогда, когда числитель будет кратным знаменателю:
(n²-4)/(n+3)=(n-2)(n+2)/(n+3)
Смотрим на числитель и знаменатель.
1) При четном значении х: числитель - четный, знаменатель - не четный;
2) При не четном значении х: числитель - не четный, знаменатель - четный.
При таком раскладе очевидно, что дробь принимает целые значения при нулях числителя х=±2, а также при знаменателе равному ±1, то есть х=-4. Если не ошибаюсь, то это и будут все значения...
Ответ: х₁=-4, х₂=-2, х₃=2.
Найдите значение дроби:
1)
8¹⁶
_______
16¹²
при а = -2. Б= -0,1
2)
15а² - 10аб
__________
3аб - 2Б²
3)9с² -4Б
______________
18с² - 12БС
Решение: $$ \frac{8^{16}}{16^{12}}=\frac{(2^{3})^{16}}{(2^{4})^{12}}=\frac{2^{48}}{2^{48}}=2^{0}=1\\\frac{15a^{2}-10ab}{3ab-2b^{2}}=\frac{5a(3a-2b)}{b(3a-2b)}=\frac{5a}{b}=\frac{5*(-2)}{-0,1}=100\\\frac{9c^{2}-4b^{2}}{18c^{2}-12bc}=\frac{(3c-2b)(3c+2b)}{6c(3c-2b)}=\frac{3c+2b}{6c} $$$$ 1) \frac{ 8^{16} }{ 16^{12} } = \frac{(2^{3})^{16}}{(2^{4})^{12}} = \frac{2^{48}}{2^{48}}=1 \\ 2) \frac{15a^{2}-10ab}{3ab-2b^{2}}= \frac{5a(3a-2b)}{b(3a-2b)} = \frac{5a}{b} \\ a=-2;b=-0,1; \frac{5a}{b}= \frac{5*(-2)}{-0,1}= \frac{-10}{-0,1}=100 \\ 3) \frac{9c^{2}-4b}{18c^{2}-12bc}= \frac{9c^{2}-4b}{3c(6c-4b)} \\ $$
Найдите значение дроби :
1. \( \frac{12,7^{2} - 5,3^{2} }{5*0,96 + 2,6} \)
2.\( \frac{3,6^{2} + 7,2 * 15,4 + 15,4^{2}}{1,9(13,2 - 3,7)} \)
Решение: 1)$$ \frac{12,7^{2}-5,3^{2}}{5\cdot0,96+2,6}= \\ =\frac{(12,7-5,3)(12,7+5,3)}{4,8+2,6}= \\ =\frac{7,4\cdot18}{7,4} $$=182)$$ \frac{3,6^{2}+7,2\cdot15,4+15,4^{2}}{1,9\cdot(13,2-3,7)}= \\ =\frac{3,6^{2}+2\cdot3,6\cdot15,4+15,4^{2}}{1,9\cdot(9,5)}= \\ =\frac{(3,6+15,4)^{2}}{1,9\cdot9,5}= \\ =\frac{(19)^{2}}{1,9\cdot9,5}= \ \frac{19\cdot19}{1,9\cdot9,5}=20 $$
Найдите значение дроби*______*
Решение: ответа) 10/13
б) 4
д) 5 32/37
а) в числителе : (7 во 2 степени = 49 ) 49+35-24=60
знаменатель : 49+35-6=78
60/78 ( сокрашаем на 6) получаем 10/13
б) в числителе: 0+0-24=-24
в знаменателе: 0+0-6=-6
-24/-6 =4
д) в числителе: 0,25+2,5-24=-21,7
в знаменателе: 0,25+2,5-6=-3,7
-21,7/-3,7=5 32/37

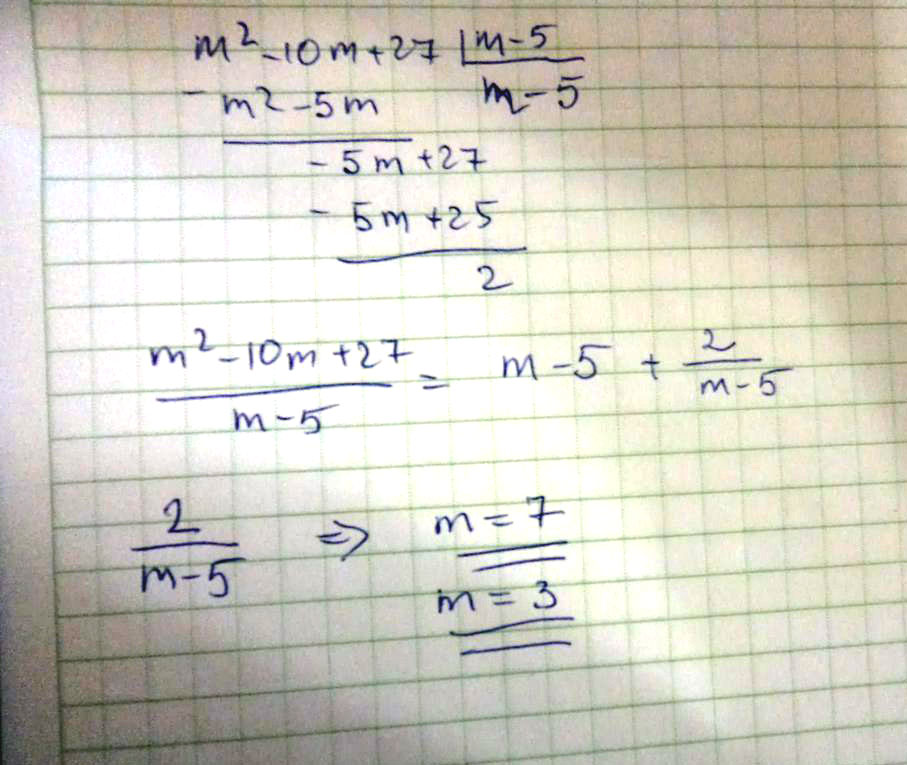
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...