дроби »
найдите значение дроби - страница 3
Найдите значение дроби номер 80 з
Решение: В этом задании главное - знать свойства степени, при условии, что одно и то же число возводится в разную степень, т. е. с делением и умножением
( при умножении степени складываются,
при делении - вычетаются).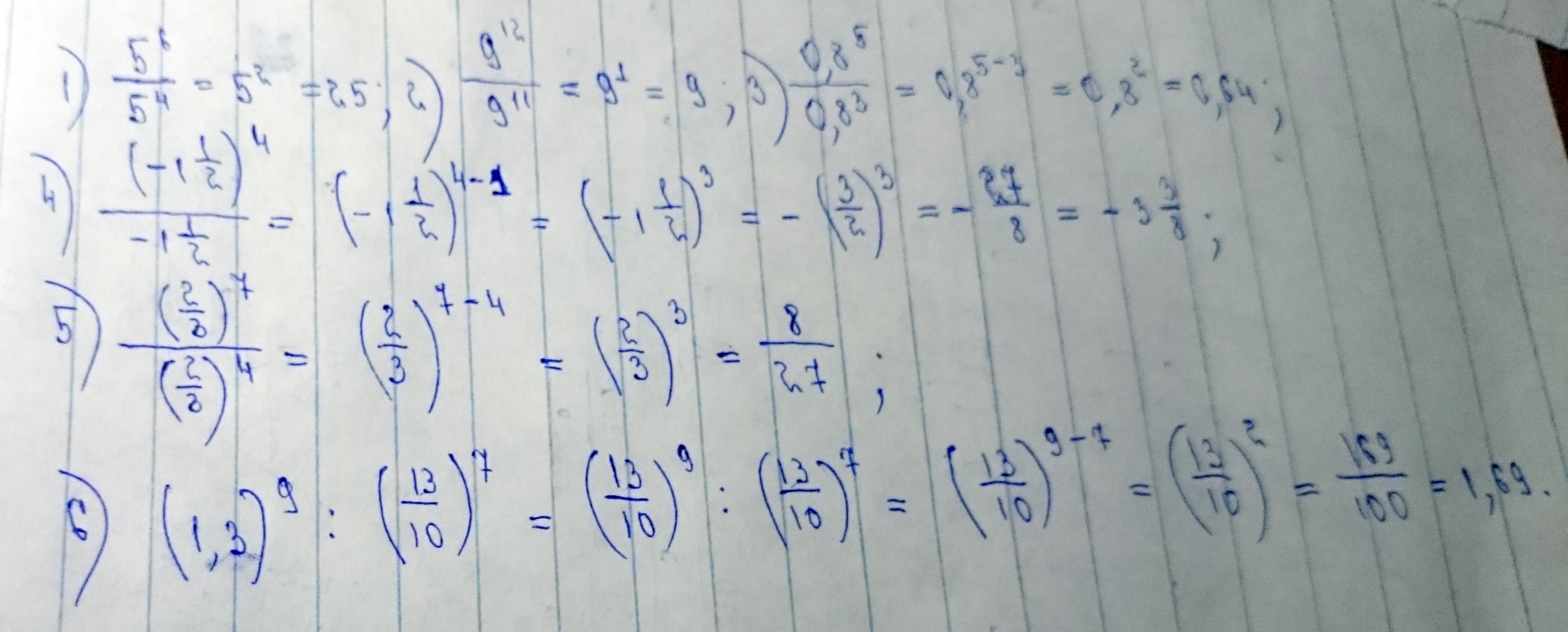
Найдите значение дроби х^2-5xy+y^2/x+y+2 при х= 3 +корень из 5 и у= 3 -корень из 5
Решение: Числитель делим на y^2, будет
(x/y)^2 - 5*(x/y) + 1
Найдем
$$ \frac{x}{y} = \frac{3+ \sqrt{5} }{3- \sqrt{5} } = \frac{(3+ \sqrt{5})^2}{(3+ \sqrt{5})(3- \sqrt{5})} = \frac{9+6 \sqrt{5} +5}{9-5}= \frac{14+6 \sqrt{5} }{4} = \frac{7+3 \sqrt{5} }{2} $$
Тогда числитель равен
$$ (\frac{7+3 \sqrt{5} }{2})^2-5*\frac{7+3 \sqrt{5} }{2}+1= \frac{49+42 \sqrt{5}+45}{4} - \frac{35+15 \sqrt{5} }{2} +1= \\ = \frac{94+42 \sqrt{5} }{4}- \frac{35+15 \sqrt{5} }{2} +1= \frac{47+21 \sqrt{5}-35-15 \sqrt{5}+2 }{2}= \frac{14+6 \sqrt{5} }{2} = 7+3 \sqrt{5} $$
Знаменатель тоже делим на y^2, будет
(x+y+2)/y^2
Найдем
$$ y^2=(3- \sqrt{5} )^2=9-6 \sqrt{5}+5=14-6 \sqrt{5} $$
Тогда знаменатель равен
$$ \frac{x+y+2}{y^2} = \frac{3+ \sqrt{5}+3- \sqrt{5} +2 }{14-6 \sqrt{5} }= \frac{8}{14-6 \sqrt{5}} = \frac{4}{7-3 \sqrt{5} } $$
А вся дробь равна
$$ \frac{7+3 \sqrt{5}}{ \frac{4}{7-3 \sqrt{5}} } = \frac{(7+3 \sqrt{5})(7-3 \sqrt{5})}{4} = \frac{49-9*5}{4}= \frac{49-45}{4} =1 $$Найдите значение дроби: ( если можете объяснить, то объясните хотя бы один пример)
1) 5a в 3 степени - 10a во 2 степени, деленное на (a-2) во 2 степени. при a=1.8
2) 2abc-ac во 2 степени, деленное на 2b во 2 степени-bc, при a= -1 целая 2/3; b= 1/6; c=1/2
Решение: 1) $$ \frac{5 \alpha^{3} - 10\alpha^{2}}{(a-2)^{2}}, \alpha = 1.8 $$
Упростим выражение(сначала выносим за скобки множитель 5a², далее делим выражение на (a - 2):
$$ \frac{5 \alpha^{3} - 10\alpha^{2}}{(a-2)^{2}} = \frac{5\alpha^{2}(\alpha - 2)}{(a-2)^{2}} = \frac{5\alpha^{2}}{(a-2)} $$
Теперь посчитаем упрощённое выражение:
$$ \frac{5 * 1.8 ^{2}}{(1.8-2)} = \frac{5 * 3.24}{-0.2} = -\frac{16.2}{0.2} = 81 $$
2) Подставляем значения и считаем:
$$ \frac{2-1\frac{2}{3}*\frac{1}{6}*\frac{1}{2} - (-1\frac{2}{3}*\frac{1}{2}^{2})}{2 * \frac{1}{6}^{2} -\frac{1}{6}*\frac{1}{2}} = \frac{2-\frac{5}{3}*\frac{1}{6}*\frac{1}{2} +\frac{5}{3}*\frac{1}{4}}{2 * \frac{1}{36} -\frac{1}{6}*\frac{1}{2}} =\\= \frac{2-\frac{5}{36} +\frac{5}{12}}{\frac{2}{36} -\frac{1}{12}} = \frac{\frac{72}{36}-\frac{5}{36} +\frac{15}{36}}{\frac{2}{36} -\frac{3}{36}} = \frac{\frac{82}{36}}{-\frac{1}{36}} = \frac{82 * (-36)}{36} = -82 $$Найдите значение дроби:
Решение: A-2/a :
1) 1-2/1= -1/1=1
2) 2 целых одна вторая-2/ 2 целых одну вторую= 0,5/ 5/12<-(здесь дробное)= 6/5= 1,2
3) 0,4-2/0,4= -1,6/0,4=-4
4) 0,5-2/0,5= -1,5/0,5= -3
5)-1,5-2/-1,5= -3,5/-1,5= 2 целых одна третья
m+12/3m-4
1) 0,5+12/3*0,5-4= 12,5/-2,5= -5
2)2+12/3*2-4= 14/2=7
3) одна третья+12/ 3*одну третью-4= 12 целых одна третья/ -3= тридцать семь третьих/ - одну третью= тридцать семь девятых= 4 целых одна девятая.
А дальше сам(а) по образцу!Найдите значение дроби: 1) \(\frac{72}{13^2-11^2};\) 2) \(\frac{79^2-65^2}{420}\); 3) \(\frac{92^2-48^2}{27^2-17^2}\); 4) \(\frac{63^2-27^2}{83^2-79^2}\)
Решение: 1) 72/(13-11)(13+11)=72/(2*24)=36/24=3/2=1,5
2)(79-65)(79+65)/420=14*144/420=144/30=4,8
3)(92-48)(92+48)/(27-17)(27+17)=44*140/(10*44)=14
4)(63-27)(63+27)/(83-79)(83+79)=36*90/(4*162)=9*10/18=5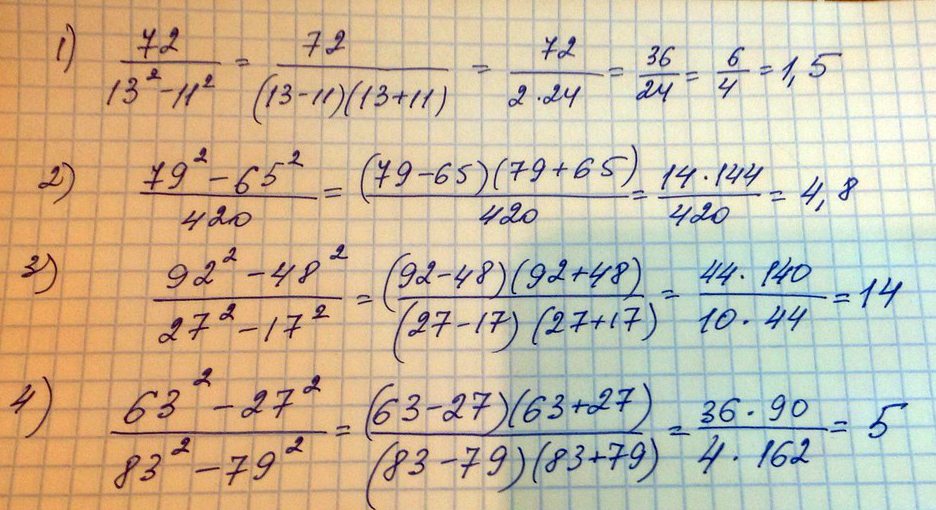

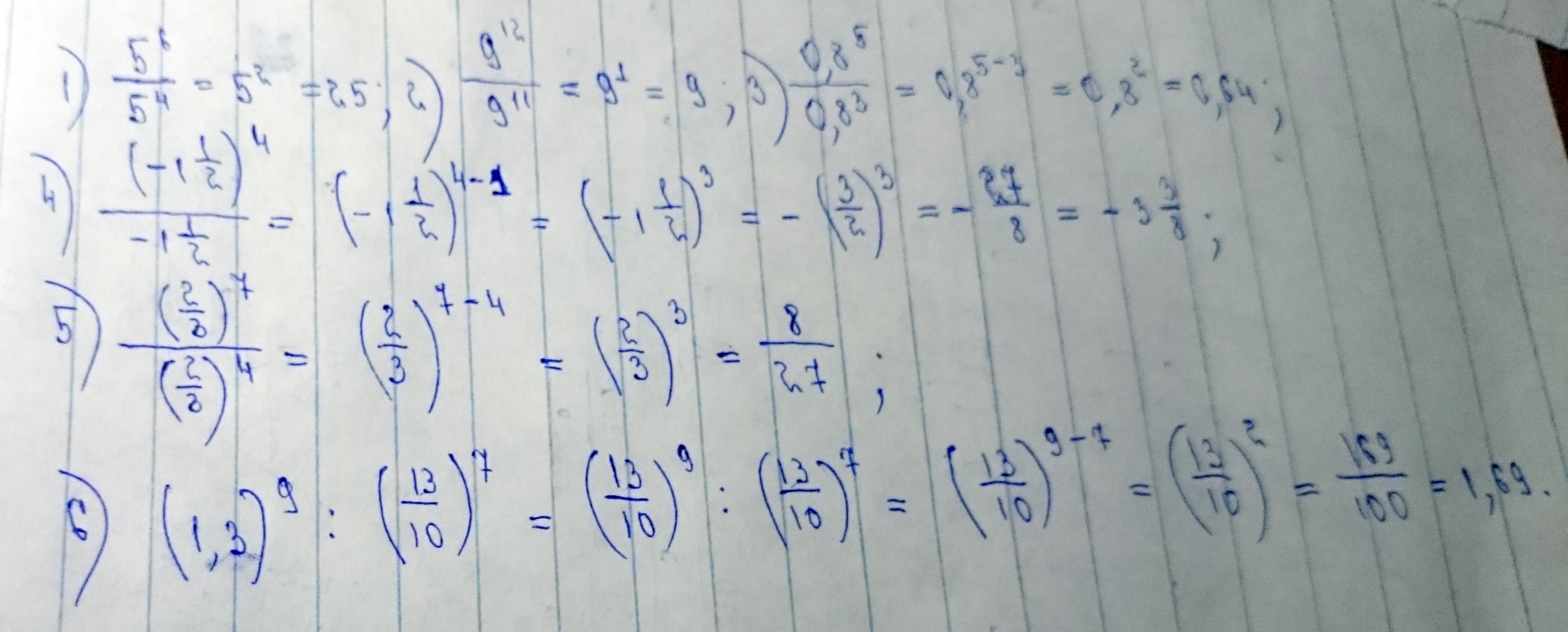
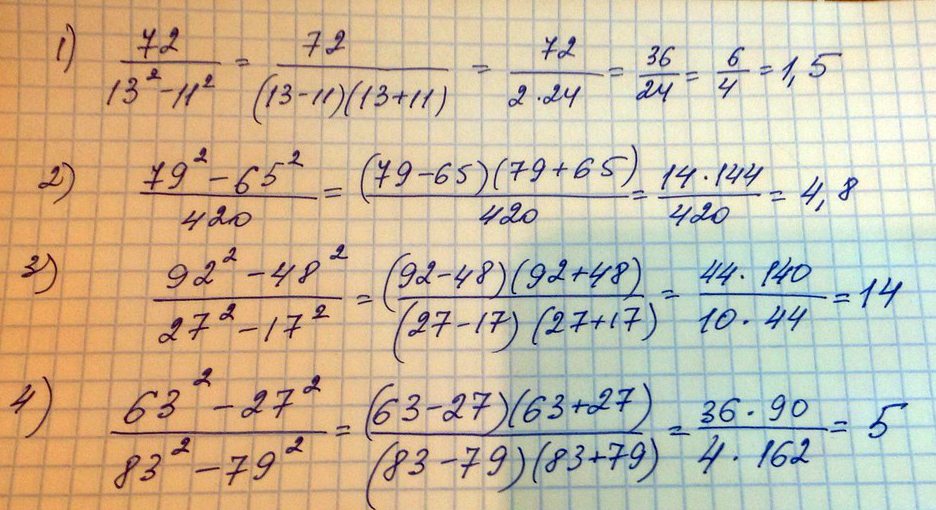
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...