дроби »
найдите значение дроби - страница 4
Найдите значение дроби x-3y/6x^2-54y^2, если x+3y=1/4
Решение:$$ \frac{x-3y}{6 x^{2} -54y ^{2} } = \frac{x-3y}{6( x^{2} -9y ^{2} )} = \frac{x-3y}{6(x-3y)(x+3y)} = \frac{1}{6(x+3y)} \\ \\ x+3y= \frac{1}{4} \\ \\ \\ \frac{1}{6* \frac{1}{4} } = \frac{1}{ \frac{6}{4} } = \frac{1}{ \frac{3}{2} } =1: \frac{3}{2} = \frac{2}{3} $$
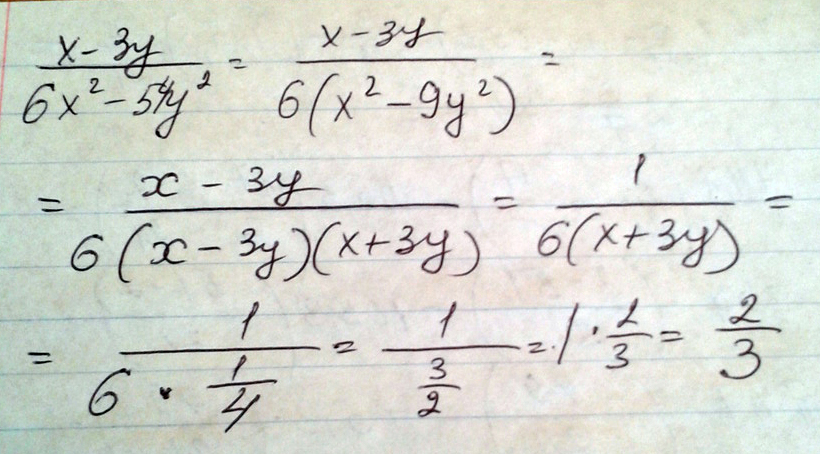
Найдите значение дроби
а)\( \frac{ \sqrt[4]{49} }{ \sqrt[4]{3} } \)
б)\( \frac{ \sqrt[5]{2}}{ \sqrt[5]{486} } \)
в)\( \frac{ \sqrt[6]{729} }{ \sqrt[3]{1728} } \)
г)\( \frac{ \sqrt[5]{3125}}{ \sqrt[10]{1024} } \)
д)\( \frac{ \sqrt[6]{2 \sqrt{2} } }{ \sqrt[5]{2 \sqrt[4]{2} } } \)
е)\( \frac{ \sqrt[4]{5 \sqrt[3]{5} } }{ \sqrt[5]{5 \sqrt[3]{25} } } \)
Решение: A) $$ \frac{ \sqrt[4]{49} }{ \sqrt[4]{3} } = \frac{49^{ \frac{1}{4} } }{3^{ \frac{1}{4} } } = (\frac{49}{3}) ^{ \frac{1}{4}- \frac{1}{4} } =(\frac{49}{3}) ^{ 0 } =1 $$
б) $$ \frac{ \sqrt[5]{2} }{ \sqrt[5]{486} } = \frac{2^{ \frac{1}{5} } }{486^{ \frac{1}{5} } } = (\frac{2}{486}) ^{ \frac{1}{5}- \frac{1}{5} } =(\frac{2}{486}) ^{ 0 } =1 $$
в) $$ \frac{ \sqrt[6]{729} }{ \sqrt[3]{1728} } =\frac{ \sqrt[6]{ 3^{6} } }{ \sqrt[3]{ 12^{3} } } = \frac{3}{12} = \frac{1}{4} $$
г) $$ \frac{ \sqrt[5]{3125} }{ \sqrt[10]{1024} } = \frac{ \sqrt[5]{ 5^{5} } }{ \sqrt[10]{ 2^{10} } } = \frac{5}{2}=2,5 $$
д) $$ = \frac{2^{ \frac{3}{12} }}{2^{ \frac{5}{20} }} = \frac{2^{ \frac{1}{4} }}{2^{ \frac{1}{4} }} =2^{ \frac{1}{4}- \frac{1}{4}}=2^{0}=1 $$
е) $$ \frac{ \sqrt[4]{5 \sqrt[3]{5} } }{ \sqrt[5]{5 \sqrt[3]{25} } } = \frac{ \sqrt[4]{\sqrt[3]{5^{4}} } }{ \sqrt[5]{ \sqrt[3]{5^{5}} } } = \frac{ \sqrt[12]{ 5^{4} } }{ \sqrt[15]{ 5^{5} } } = \ = \frac{5^{ \frac{4}{12} }}{5^{ \frac{5}{15} }}= \frac{5^{ \frac{1}{3} }}{5^{ \frac{1}{3} }} =5^{ \frac{1}{3}- \frac{1}{3}}=5^{0}=1 $$Найдите значение дроби
Решение:⁴√5³√5÷ ⁵√5³√25= 5 ÷ 5 =5 =5 = 1
1) Найдите значение дроби : x-8/x²-64 при x=2
2) решите неравенство : x²+2x-48<0
Решение: x-8/x²-64 при x=2$$ \frac{x-8}{x^{2}-64} = \frac{x-8}{(x-8)(x+8)} = \frac{1}{(x+8)} $$
Подставляем число:
$$ \frac{1}{(2+8)} = \frac{1}{10} = 0,1 $$
2)
x²+2x-48<0
x²+2x-48=0
x1=-8
x2=6
________-8_______________6_______
+ - +
Ответ: X∈(-8;6)
1) Найдите значение дроби:
\frac{9 x^{2}-3xy }{12xy-4y x^{2} } При x=0,5, y=0,25;
2) Сократите дробь:
\( \frac{a ^{2}+2bc-b ^{2}-c ^{2} }{b ^{2}-a ^{2}-c ^{2}+2ac } \)
Решение: $$ \frac{x^2-y^2}{2y^2} \cdot \frac{xy+y^2}{(x+y)^2} \\ \frac{(a+b)^3+(a-b)^3}{2ab(a^2+3b^2)} - 1 \\ \frac{(a^2-ab+b^2)(a+b)^2(a-b)}{(a^3+b^3)(a^2-b^2)}$$(a+b)^3+(a-b)^3 / (2ab(a^2+3b^2)) - 1 ==( a^3+3a^2b+3ab^2+b^3 + a^3-3a^2b+3ab^2-b^3) /(2ab(a^2+3b^2)) - 1 ==(2a^3+6ab^2) /(2ab(a^2+3b^2)) -(2ab(a^2+3b^2)) /(2ab(a^2+3b^2)) ==(2a(a^2+3b^2) -2ab(a^2+3b^2)) /(2ab(a^2+3b^2)) ==(2a-2ab)(a^2+3b^2) /(2ab(a^2+3b^2)) = (2a-2ab) /(2ab)=2a(1-b)/(2ab)== (1-b) / b

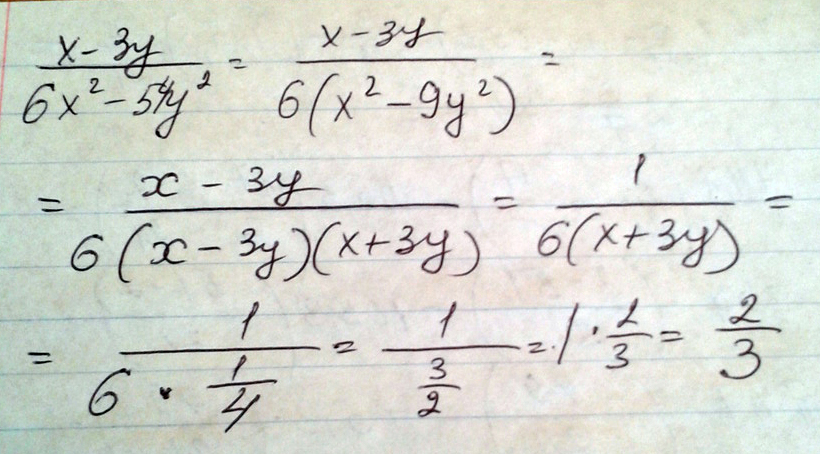
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...