найдите значение дроби - страница 2
Найдите значение дроби
71² - 15² + 86×24
63-23²
Решение: Числитель преобразуем сначала по формуле разность квадратов : 71²-15² = (71-15) * (71+15) =56*86.
Числитель примет вид 56*86 + 86 *24 = 86 (56+24) = 86*80
Полагаю, что в условии есть опечатка(в знаменателе) должно быть 63²-23², тогда 63²-23²=( 63-23 ) *(62+23) = 40*86.
Следовательно получаем 86*80 / 40*86 = 2
Ответ :2Найдите значение дроби: пж))))))) 92^2-48^2/27^2-17^2
Решение: решение во вложенном файле!Приминяем формулу сокращённого умнажения:
(92-48)(92+48)/(27-17)(27+17), получаем
44*140/10*44, скоращаем
получается 14
Ответ: 14.
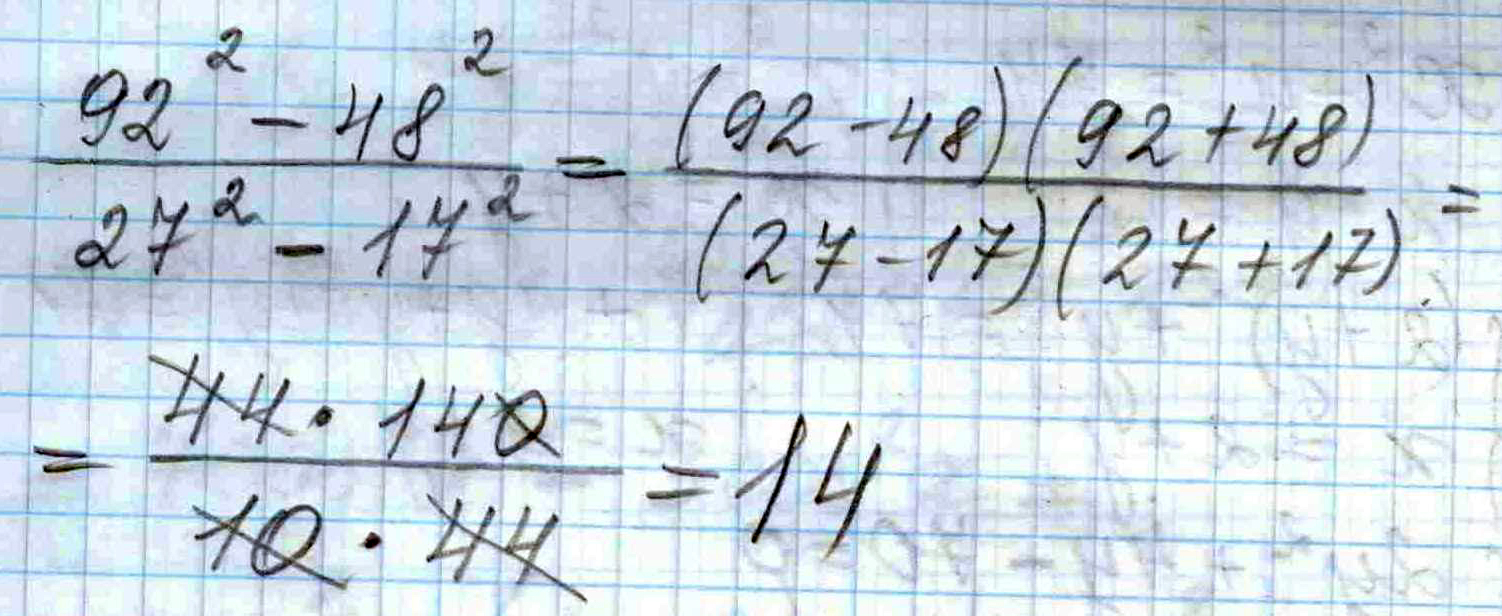
найдите значение дроби 4x^2+8x-32/4x^2-16 при x = -1 ; 5 ; 10
Решение: Дана дробь 4x^2+8x-32 ; разложим на множители квадратный трёхчлен:
4x^2-16
4х^2+8x-32=0
D=8^2-4*4*(-32)=64+512=576, квадратный корень из 576 равен 24,
x1=(-8)+24/8=16/8=2
x2=(-8)-24/8=-32/8=-4
4х^2+8x-32=2(x-2)(x+4)=(2x-4)(2x+8)
Разложим знаменатель как разность квадратов:
4x^2-16=(2x-4)(2x+4)
Сокращаем на 2x-4 и получаем следующее: 2х+8
2х+4
Если х=-1, то 2(-1)+8/2(-1)+4=6/2=3
Если х=5, то 2*5+8/2*5+4=9/7 или одна целая 2/7
Если х=10, то 2*10+8/2*10+4=7/6 или одна целая 1/6
Найдите значение дроби при x=-4;y=-0,1
Решение: Вроде бы все видно достаточно хорошо
а)6х*(3х-5у) 6х 6*(-4) -24
- =-= - = - =240
у*(3х-5у) у (-0,1) -0,1
б)(х+5у)^2 х+5у -4+5*(-0,1)
-=-=-= -1,5
3*(х+5у) 3 3
в)(2х+3у)*(2х-3у) 2х+3у 2*(-4)+3*(-0,1) -8+(-0,3) -8,3 83
-=-=-=-= -=-=
6ху*(2х-3у) 6ху 6*(-4)*(-0,1) 2,4 2,4 24
= -3 11/24
г)(х+у)*(х+у) х+у -4+(-0,1) -4,1 41
-=-=-=-=-=1 2/39
(х-у)*(х+у) х-у (-4)-(-0,1) -3,9 39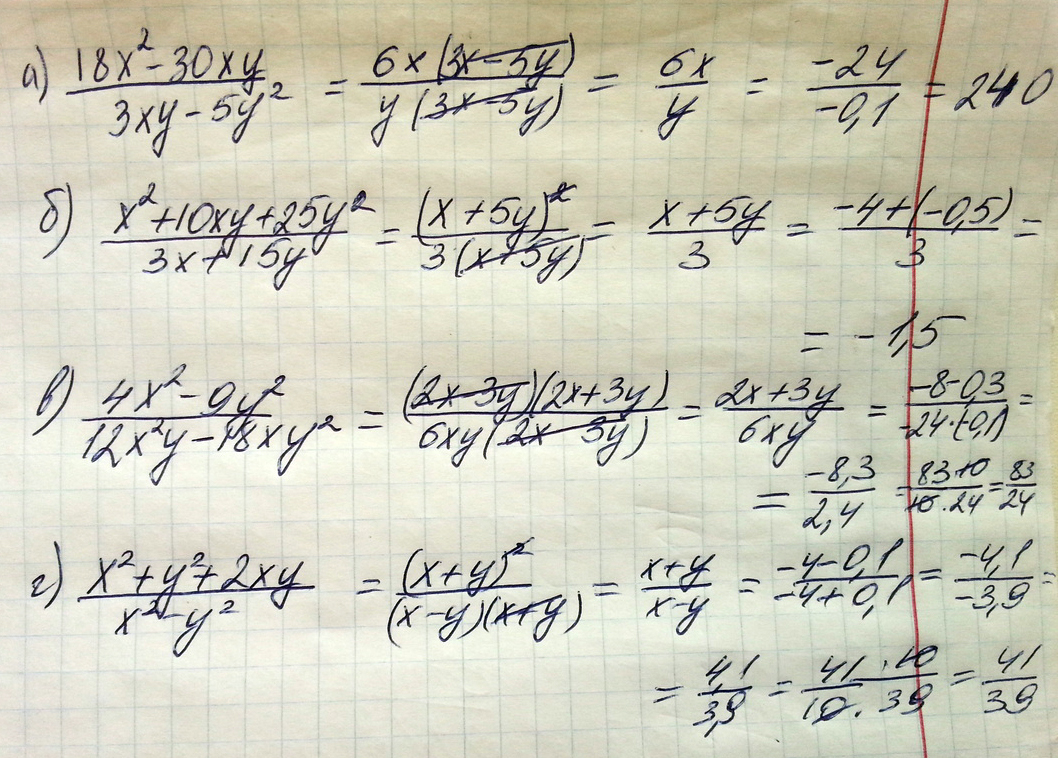
Найдите значение дроби предворительно сократив её 20/45+26/54, 14/24-39/90+15/100, 45/72-33/144-20/64
Решение: 1) 25/27
2)3/10
3)1/12$$ \frac{20}{45} + \frac{26}{54} = \frac{4}{9} + \frac{13}{27} = \frac{4*3}{9*3} + \frac{13}{27} = \frac{12+13}{27} = \frac{25}{27} \\ \frac{14}{24}- \frac{39}{90} + \frac{15}{100} = \frac{7}{12} - \frac{13}{30} + \frac{3}{20} =\frac{7*5}{12*5} - \frac{13*2}{30*2} + \frac{3*3}{20*3} = \frac{35-26+9}{60} = \frac{18}{60} $$ $$ = \frac{3}{10} \\ \frac{45}{72} - \frac{33}{144} - \frac{20}{64} = \frac{5}{8} - \frac{11}{48}- \frac{5}{16} = \frac{5*6}{8*6} - \frac{11}{48}- \frac{5*3}{16*3} = \frac{30-11-15}{48} = \frac{4}{48} = \frac{1}{12} $$

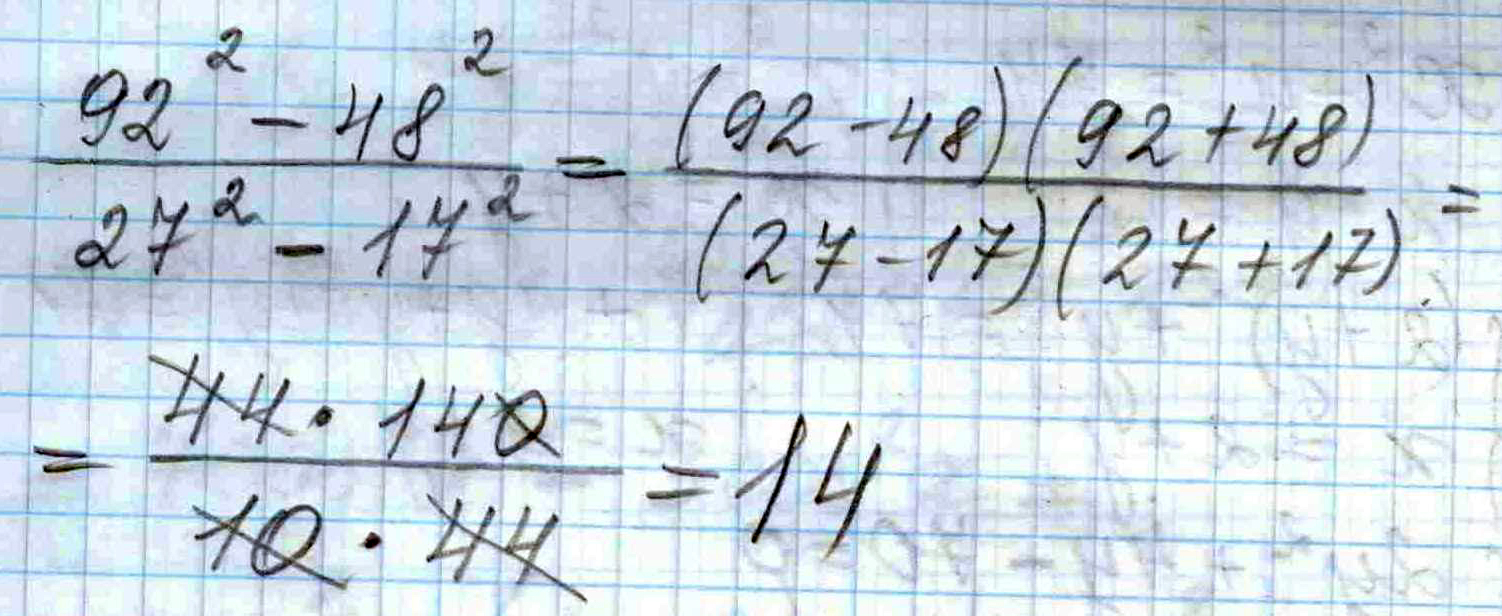
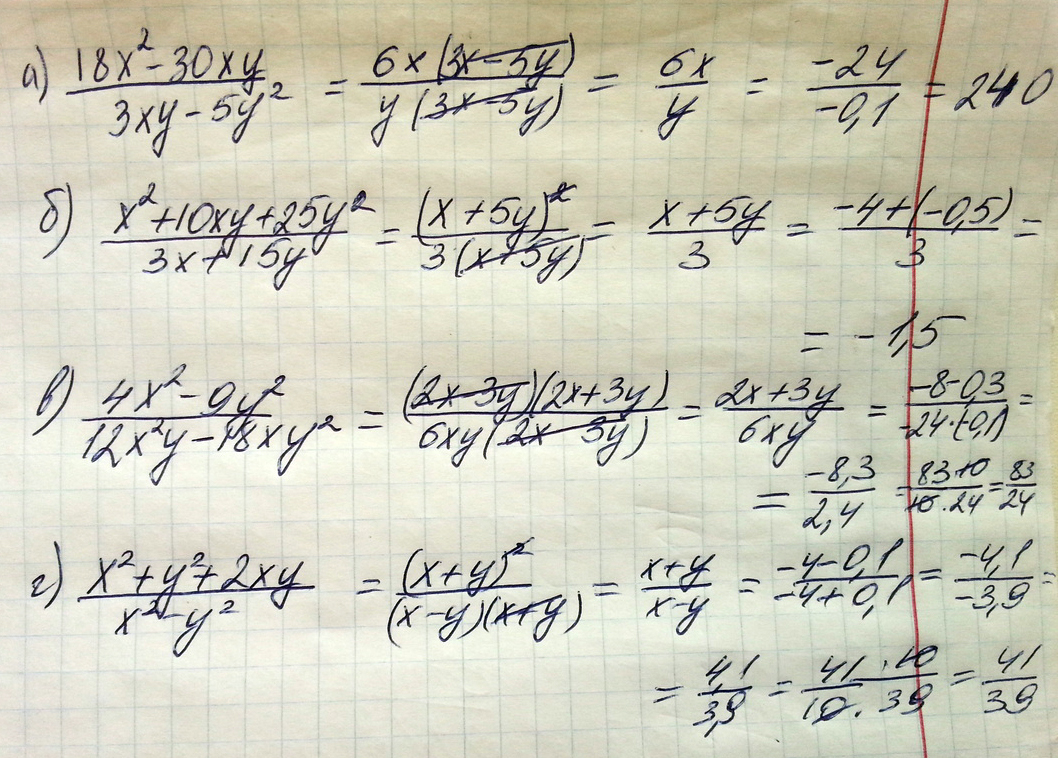
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...