основное свойство дроби - страница 2
Используя основное свойство дроби, найдите значение х:
7х-9/12=35/84
Решение: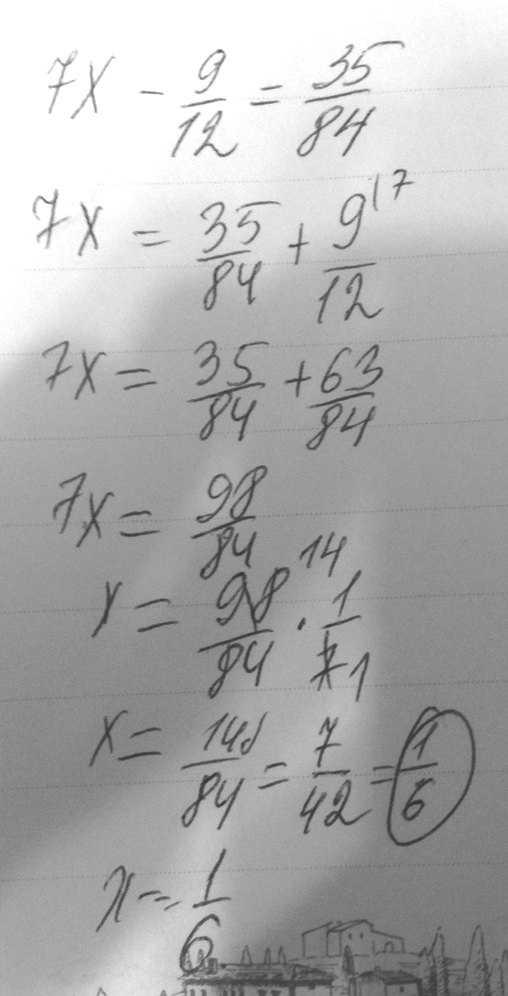
Используя основное свойство дроби, найдите значение a, при котором равенство a/8=15/40
Решение: Правило, называемое основным свойством дроби.
"Числитель и знаменатель дроби можно умножать или делить на одно и то же натуральное число, от чего величина дроби не изменяется".
Если числитель новой дроби представить произведением (или частным) первой дроби и любого натурального числа, а знаменатель новой дроби — произведением (или частным) знаменателя первой дроби и того же числа, то новая дробь сохраняет при вычислении произведений (или частных) значение (величину) исходной дроби, поэтому между заданной и полученной дробью можно ставить знак равенства.
Можно записать основное свойство дроби при умножении числителя и знаменателя дроби на число
например: 3/7=3*3/7*3=9/21следовательно 3/7=9/21
Можно записать основное свойство дроби при делении числителя и знаменателя дроби на число
например: 45/105=45:3/105:3=15/35 следовательно 45/105=15/35А=3, там пропорция!
умножай правую часть на 8 (ну получается, что ты обе части умножаете на 8)
потом сокращаете дробь
и получается
2)3
Запишите дроби 1\3, 2\3, 3\4, 1\6 в виде дроби со знаменателем 12 Какое свойство дроби для этого можно использовать
Решение: 1/3 2/3 3/4 1/6 = 4/12 8/12 9/12 2/12
Это называется привести дроби к общему знаменателю, для этого находится наименьшее общее кратное(число которое делится без остатка на все наши знаменатели), в данном случае это 12.
Делим 12 на знаменатель каждой дроби и то, что получится умножаем на числитель этой дроби и записываем в числитель, а в знаменателе оставляем 12.
12 : 3 = 4 ; 4*1 = 4 ; 4/12
12 : 3 = 4 ; 4*2 = 8 ; 8/12
12 : 4 = 3 ; 3*3 = 9 ; 9/12
12 : 6 = 2 ; 2*1 = 2 ; 2/12Напишите свойства по математике словесной форме и в форме примера. СВойства(переместительное(• и +), сочетательное(• и+), распределительное((•,+) и (•,), (:,+) и (:,)), основное свойство дроби)
Решение: 1) переместительный: от перемены мест слагаемых (множителей) сумма (произведение) не меняется.a + b = b + a; 7+12=12+7
a * b = b * a; 5·2=2·52) сочетательный:
a + (b + c)=(в+b)+c
чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое.
(14+17)+103=14+(17+103)
(a * b) * c = a * (b * c) чтобы произведение двух множителей умножить на третий множитель, можно первый множитель умножить на произведение второго и третьего множителей.
(15·2)·5=15·(2·5)
3) распределительный: Чтобы сумму умножить на число, можно умножить на это число каждое из слагаемых, а затем сложить полученные произведения.
(a + b) * c = a * c + b * c
(18+7)·2=18·2+7·2
Основное свойство дроби это-
Решение: Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. Это свойство называют основным свойством дроби. Например: 2 3 = 2•3 3•3 = 6 9 ; 3 4 = 3•2 4•2 = 6 8. Две равные дроби являются различными записями одного и того же числа.
$$ \left[\begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right] $$Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

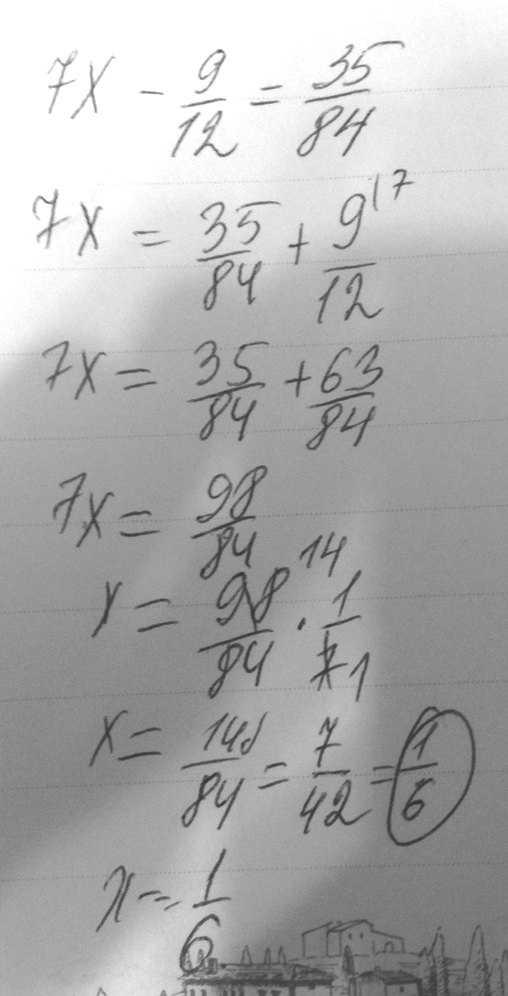
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...