числитель и знаменатель дроби
1. правило разложения чисел на простые множители нахождение НОД и НОК чисел?
2. основное свойство дроби-значение дроби не изменится, если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю?
Решение: 1. Алгоритм разложения числа на простые множители следующий:
Текущий делитель = 2.
Проверяем, делится ли число на текущий делитель. Если делится, то делим и проверяем снова. Если не делится, то увеличиваем текущий делитель на 1. Повторяем до тех пор, пока в результате деления не получим 1 или пока результат деления не совпадет с делителем.
Пример:
72 = 2 * 36 = 2 * 2 * 18 = 2 * 2 * 2 * 9 = 2 * 2 * 2 * 3 * 3;
На первых трех шагах делили на 2, пока не получили в результате деления 18 на 2 число 9. Оно не делится на два, проверяем следующий делитель = 3. В это примере результат деления совпал с текущим делителем.
Если же число простое, например 17, то
17 = 17 * 1;
мы остановимся, когда в результате деления увидим единичку.
НОД нескольких чисел найти несложно. Раскладываем каждое на простые множители, как описано выше, затем выбираем из разложения те, которые повторяются для ВСЕХ чисел.
Пример:
16 = 2 * 2 * 4 = 2 * 2 * 2 * 2
42 = 2 * 21 = 2 * 3 * 7
24 = 2 * 12 = 2 * 2 * 6 = 2 * 2 * 2 * 3
Общей для всех является только одна 2, значит, НОД = 2.
Если бы вместо 42 было число 84
84 = 2 * 42 = 2 * 2 * 21 = 2 * 2 * 3 * 7
то НОД был бы 2 * 2, т. к. в этом случае ОБЩИМИ были бы уже две двойки
НОК можно найти используя НОД: произведение всех чисел делим на НОД.
2. Да, это верно. Оно используется при приведении дробей к общему знаменателю.
3. Это не совсем дробь, корректнее назвать это частью числа или процентами числа. Перевод частей в проценты так же не составляет сложности - просто умножаем число частей на 100. Например, 0.23 = 0.23 * 100 = 23 процента.
0.23 * 200 - нахождение 23 процентов от числа 200.Выберите верное утверждения.
1) Если числитель и знаменатель дроби умножить на 5, то дробь не изменится.
2) Если знаменатель положительный дроби увеличить в 2 раза, то дробь уменьшится в 2 раза.
3) При умножении двух нецелых чисел всегда получается нецелое число.
4) Если к числителю и знаменателю дроби прибавить 2, то дробь не изменится.
Решение: 1) верно
2) верно
3) неверно.
Пример: 0,2*0,5=1 (0,2 и 0,5 - нецелые числа, но их произведение - целое число)
4) неверно.
Пример:
Возьмём дробь 5/7.
Если к числителю и знаменателю одновременно прибавить 2, получим дробь 7/9. Приведём дроби к одному знаменателю: 5*9/7*9=45/63
7*7/9*7=49/63
45<49
45\63< 49\63
5|7 < 7|9 => 5/7≠7/9Числитель и знаменатель дроби - положительные числа. Как изменится дробь, если числитель увеличить на 17%, а знаменатель уменьшить на 48%
Решение: 1) X/Y - начальная дробь
2) Числитель увеличиваем на 17% :
Х + 0,17Х = 1,17Х
3) Знаменатель уменьшим на 48 % :
Y - 0,48Y = 0,52Y
4) получим дробь:
( 1,17X ) /( 0,52Y ) = ( 2,25X) / Y
5) как изменится дробь ?
( 2,25Х )/ Y ) : ( X/Y ) = 2,25 ( раз )
ОТВЕТ увеличится в 2,25 разаПусть числитель дроби х, знаменатель у, Числитель увеличили на 17%, он стал 1,17х, знаменатель уменьшили на 48% и он стал 0,52у
1,17х:0,52у=2,25 (х/у)
Дробь увеличилась в 2,25 разаЧислитель и знаменатель дроби-положительные числа. Как изменится дробь, если числитель увеличит на 32%, а знаменатель увеличить на 10%?
Решение: Если числитель увеличить на 32%, а знаменатель на 10%, то вся дробь увеличится в 32/10=3,2.Ответ: дробь изменится в 3,2.
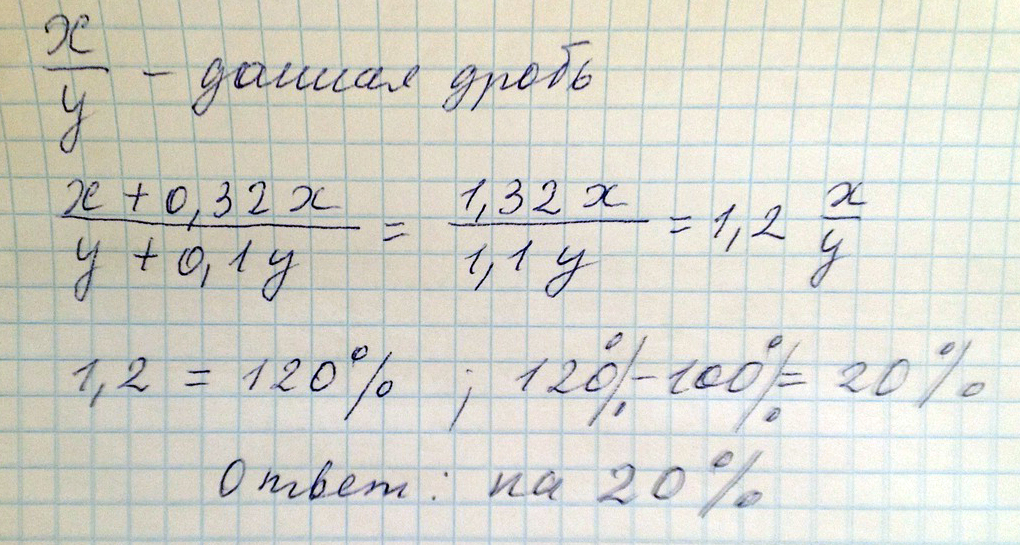
Числитель и знаменатель дроби-положительные числа. Как изменится дробь, если числитель увеличится на 32%, а знаменатель увеличить на 65%
Решение: Допустим дробь имеет вид $$ \frac{x}{y} $$, где х>0 и y >0Увеличим числитель и знаменатель $$ \frac{0,32x + x}{0,65y + y} = \frac{1,32x}{1,65y} $$ получим $$ 0,8 \frac{x}{y} $$
Дробь уменьшится до 80%
Определённой дроби у нас в условии нет (чисел), так что возьмём универсал - переменные.)
Имеется дробь:
$$ \frac{x}{y} $$
Даже сделаем так:
И в числителе и в знаменателе - числа, которые составляют 100% каждое по отдельности, то есть:
$$ \frac{x}{y}= \frac{100\%}{100\%} $$
И эти числа, кстати, да - положительные, т. е. оба > 0.
Теперь смотрим условия: числитель увеличивается на 32%, а знаменатель - на 65%. Что это означает? Это означает, что сначала нужно найти сколько составляет 32% от 100% и 65% - от 100%. Есть формула. Хотя она здесь, честно говоря, и не нужна, но всё-таки приведу для справки:
$$ b = \frac{a}{100}\cdot p $$
b - это то, что мы получим
a - это число от которого считаем
p - это проценты, которые мы по сути и переводим в конкретное число.
У нас:
b - это то, что мы получим
a - это числа, которые стоят в числителе и знаменателе (для удобства возьмём сотни ("100") за эти числа)
p - это проценты, которые указаны в условии задачи (32% и 65%).
Итак:
b₁ (числитель) = 100 : 100 × 32 = 32
b₂ (знаменатель) = 100 : 100 × 65 = 65
А теперь ещё раз читаем условие задачи: ". если числитель увеличится на 32%, а знаменатель увеличить на 65%". Надо те результаты, которые мы получили, прибавить к числам, от которых находили эти самые результаты:
1. 100 + 32 = 132 (числитель)
2. 100 + 65 = 165 (числитель)
Мы получили изменённую дробь:
$$ \frac{132}{165} $$
Остааётся только разделить полученную дробь на первоначальную, и тогда мы узнаем, на сколько же они различны, вернее ВО сколько:
$$ \frac{132}{165}:\frac{100}{100}= \frac{132}{165}\cdot 1 = \frac{132}{165}=\\\\ =\frac{132\cdot 2}{165\cdot 2}=\frac{264}{330}=\frac{264:6}{330:6}=\frac{44}{55}=\frac{44:11}{55:11}=\frac{4}{5}=0,8=\frac{8}{10} $$
0,8 - это и есть ответ. Дробь изменилась в 0,8 раз или уменьшилась до 80% (или, другими словами: уменьшилась на 20%, так как 100 - 80 = 20). Давайте проверим:
Возьмём, допустим, такую дробь:
$$ \frac{10}{15} $$
Изменяем числитель и знаменатель согласно условиям:
Теперь разделим получившуюся дробь на первоначальную:
$$ \frac{8}{15}: \frac{10}{15}=\frac{8}{15}\cdot \frac{15}{10}=\frac{8}{10} =0,8 $$
И так с любыми числами, стоящими в числителе и знаменателе.)
Ответ: в 0,8 раз или на уменьшится 20%.

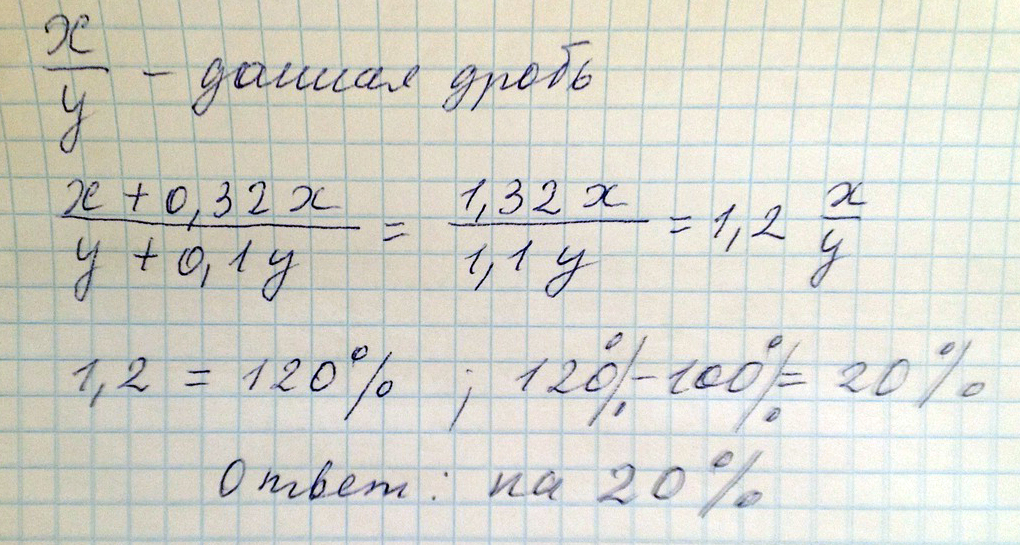
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...