дроби »
дроби с разными знаменателями
Как разделить одну дробь на другую?
2. Формула для нахождения числа по заданному значению его дроби и ее компоненты.
3. Как преобразовать обыкновенную дробь в десятичную?
4. Когда можно преобразовать обыкновенную дробь в десятичную?
5. Какие результаты можно получить при делении натуральных чисел?
6. Как найти десятичное приближение обыкновенной дроби до нужного разряда?
7. Основное свойство дроби
8. Какая дробь называется несократимой?
9. Что такое общий знаменатель двух дробей?
10. Как привести к общему знаменателю дроби?
11. Как сравнить дроби с разными знаменателями?
12. Как сложить две обыкновенные дроби?
13. Как вычесть две обыкновенные дроби?
14. Как умножить две обыкновенные дроби?
15. Какие числа называются взаимно обратными?
16. Как найти процент от числа?
17. Что называют отношением чисел а и b?
18. Сформулировать основное свойство отношения.
19. Что показывает отношение чисел а и b?
20. Что такое пропорция?
21. Сформулировать основное свойство пропорции.
22. Что такое процентное отношение двух чисел?
23. Что показывает процентное отношение?
24. Какие величины называют прямо пропорциональными?
25. Какие переменные называют обратно пропорциональными?
Решение: Частное двух чисел называют отношением этих чисел.
Так с помощью букв записывают отношение чисел a и b, причем, а – предыдущий член, b – последующий член.
Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.
Желаюлюди с вопросами по математике
1) изменится ли дробь, есле её числетель и знаменатель умножить на 15, а потом разделить на 3
2) к какому новому знаменателю мождно привести данную дробь
3) мождно ли привести дробь к знаменателю 35 и к знаменателю 25
4) какое число называют дополнительным множителем
5) как найти дополнительный множитель
6) как привести дробь к наименьшему общему знаменателю
7) как сравнить дроби с разными знаменателями
8) как выполнить вычитание дробей с разными знаменателями
9) как сложить смешанные числа
Решение: 1) нет2) делящимуся на 5
3) не всегда можно привести к знаменатель 35, так как не все числа делятся на 7(35=5*7). но всегда можно к 25.
4) наименьшее число которое я вляется делимым для двух и более чесел то есть знаменателей
5) надо найти наименьшее целое число на которое делились бы обо (и более) знаменателей
6) методом подбора
7) привести к общему знаменателю
8) привести к общему знаменателю
9) сначало привести к неправильной дроби потом привести к общему знаменателю, сложить и по возможности выделить целуу часть
Как решать дроби с разными знаменателями на сложение, вычитание, умножение и деление.
например:
5/10+8/18
5/10-8/18
5/10*8/18
5/10:8/18
Решение: З додаваням і відніманям потрібно знайти спільний знаменик ну це таке число шо ділиться на одний знаменик і на другий. В множені ми скорочуєм і перемножуєм чисельник і знаменик. А в ділені другий дріб перевиртаєм і замінюєм дію ділиня на дію множеня і множим.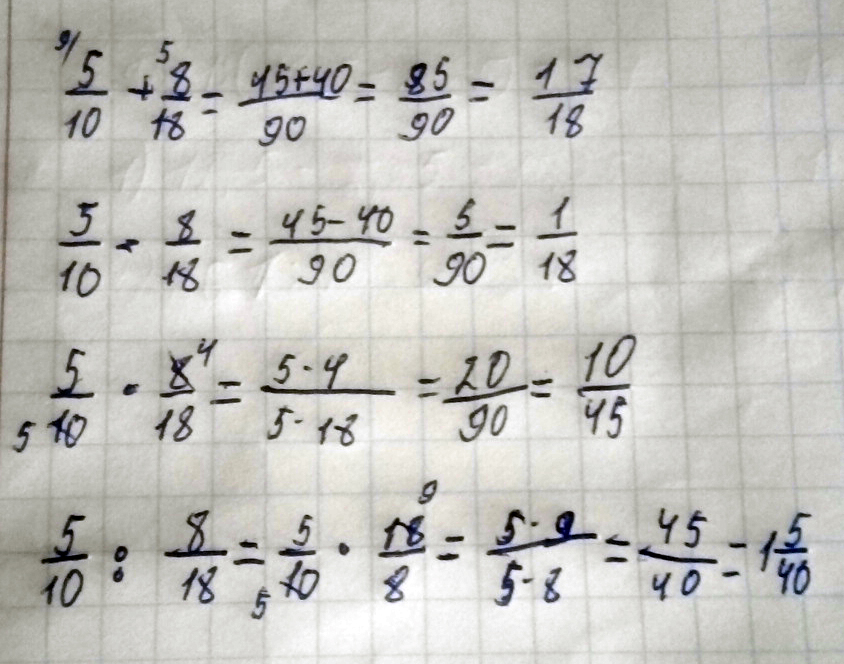
1. Сформулировать основное свойство дроби.
2. Что называют сокращением дробей?
3. Какую дробь называют несократимой?
4. Какое число называют дополнительным
множителем?
5. Как привести дроби к наименьшему общему
знаменателю?
6. Как найти дополнительный множитель?
7. Как сравнить дроби с разными знаменателями?
8. Как сложить дроби с разными знаменателями?
9. Как вычесть дроби с разными знаменателями?
10. Как складывать смешанные числа?
11. Как вычитать смешанные числа?
Решение: 1) если числ и знам. дроби умножить или : на одно и то же число, то дробь не изменится
2) деление числителя и знаменателя на одно и тоже число
3) если числитель и знаменатель не имеют общих делителей
4) частное от деления общего знаменателя на знаменатель исходной дроби
5)1. найти общий знам-ль
2. найти дополнительные множители
3. умножить знамен-ли данных дробей на дополн. множители
6) разделить общий знаменатель на знам-ль данной дроби
7) нужно привести их к общ. знам-лю и сравнить их числители
8) нужно привести их к общему знам-лю и выполнить сложение по правилу сложения дробей с одинаковыми знаменателями
9) нужно привести их к общему знам-лю и выполнить вычитание по правилу вычитания дробей с одинаковыми знаменателями
10) сложить отдельно целые части и отдельно дробные части и результаты сложить
11) вычесть отдельно целые части и отдельно дробные части и результаты сложитьЧто называют наименьшим общим знаменателем? Как привести дроби к наименьшему общему знаменателю? Как сравнить, сложить, или вычесть дроби с разными знаменателями?
Решение: НОЗ- это любое положительное число общее кратное всех знаменателей дробей, то есть это наименьшее общее число. например для дробей 2/3 + 1/2 + 5/4 НОЗом будет 12. приводятся легко например 2/3 + 5/2 смотрим на знаменатель и теперь мы должны найти общее число цифр 2 и 3 их много и ближайшее это 6, 2*3=6 и 3*2=6, или например знаменатели это 6 и 9 ближайшее их общее число 18 следовательно 6 умножаем на 3 получаем 18, а 9 на 2 что равняется 18. СРВНЕНИЕ ДРОБЕЙ если знаменатели одинаковые тогда все просто например 10/5 и 15/5 смотрим на числитель больше 51 следовательно 10/5 меньше 15/5, если знаменатели разные приводим к общему и тогда все легко сравнивается. слаживаем и вычитаем как обычные числа, но надо привести к общему знаменателю и так 5/2+6/2=11/2 или 3/2-2/2=1/2 вот и все все легко

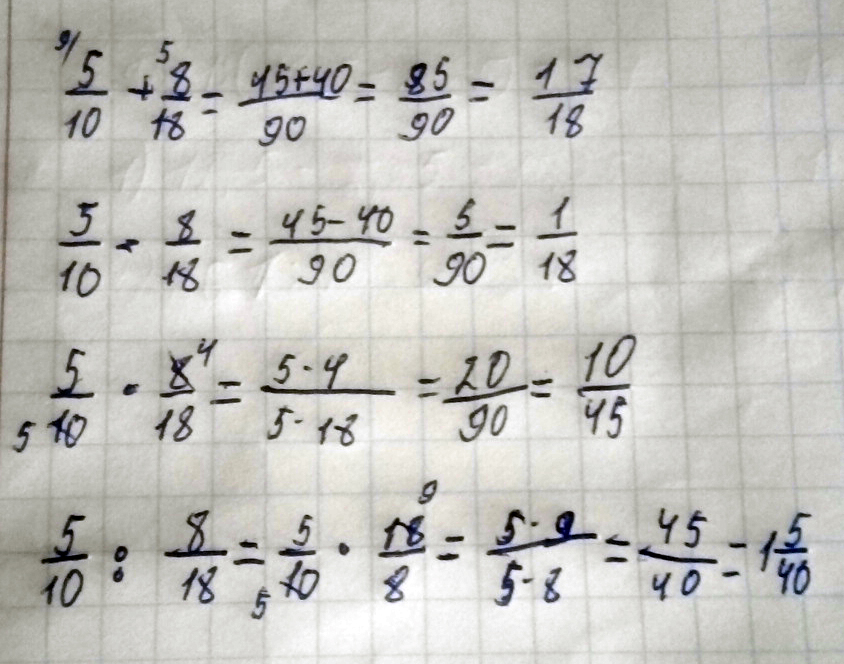
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...