числитель дроби - страница 6
Если числитель дроби умножить на 2, а из знаменателя вычесть 2, то получиться 2. Если же из числителя вычесть 4, а знаменатель умножить на 4, то получиться одна двенадцатая. Найдите эту дробь.
Решение: Пусть числитель дроби x и знаменатель дроби y, тогда дробь примет вид $$ \frac{x}{y} $$
далее составляем систему уравнений
$$ \left \{ {{ \frac{2x}{y-2}=2 } \atop { \frac{x-4}{4y}= \frac{1}{12} }} \right. $$
из первого уравнения получаем:
2x=2(y-2)
x=y-2
подставим значение x во второе уравнение:
$$ \frac{y-6}{4y}= \frac{1}{12} $$
12y-72=4y
8y=72
y=9
x=7
Искомая дробь $$ \frac{7}{9} $$Числитель дроби на 2 больше ее знаменателя. Если сложить эту дробь с обратной ей дробью, то получится число 2 4/35. Найдите исходную дробь.
Решение: Пусть числитель дроби-х, тогда знаменатель дроби - (х-2), а сама дробь -$$ \frac{x}{x-2} $$, ей обратная:$$ \frac{x-2}{x} $$. Сумма дробей равна:
$$ 2\frac{4}{35} $$
Составим и решим уравнение:
$$ \frac{x}{x-2}+\frac{x-2}{x}=2\frac{4}{35} $$ |*35x(x-2)
$$ 35x^2+35x^2-140x+140-74x^2+148x=0 \\ x=0 \\ x=2 \\ 4x^2-8x-140=0 $$ |:4
$$ x=0 \\ x=2 \\ x^2-2x-35=0 \\ x=0 \\ x=2 $$
________________________________________________________
$$ D=4+140=144 \\ x_1=\frac{2+12}{2}=7 \\ x_2=\frac{2-12}{2}=-5 $$
_________________________________________________________
x=7; x=-5
$$ x=0 \\ x=2 $$
х=7; х=-5
Получаем дроби:
1)$$ \frac{5}{7} $$
2)$$ 1\frac{2}{5} $$
Условие задачи удовлетворяет вторая дробь: $$ 1\frac{2}{5} $$
Ответ: $$ 1\frac{2}{5} $$
Числитель дроби 1 3\5 : 0.8 + (1 1\2) в кубе * 0.8
знаменатель 0.6 - 0.6 * 1 1\6
Решение: Числитель: переводим 1 3/5 в десятичную дробь =1,61,6/0,8=2
(1 1/2) в кубе =1 1/8
переводим в десятичную дробь =1,125
1,6+1,125=2,725
знаменатель:
6/10 * 7/6=7/10=0,7
0,6-0,7= -0,1
1,125/(-0,1)= -11.25
Ответ: -11,25
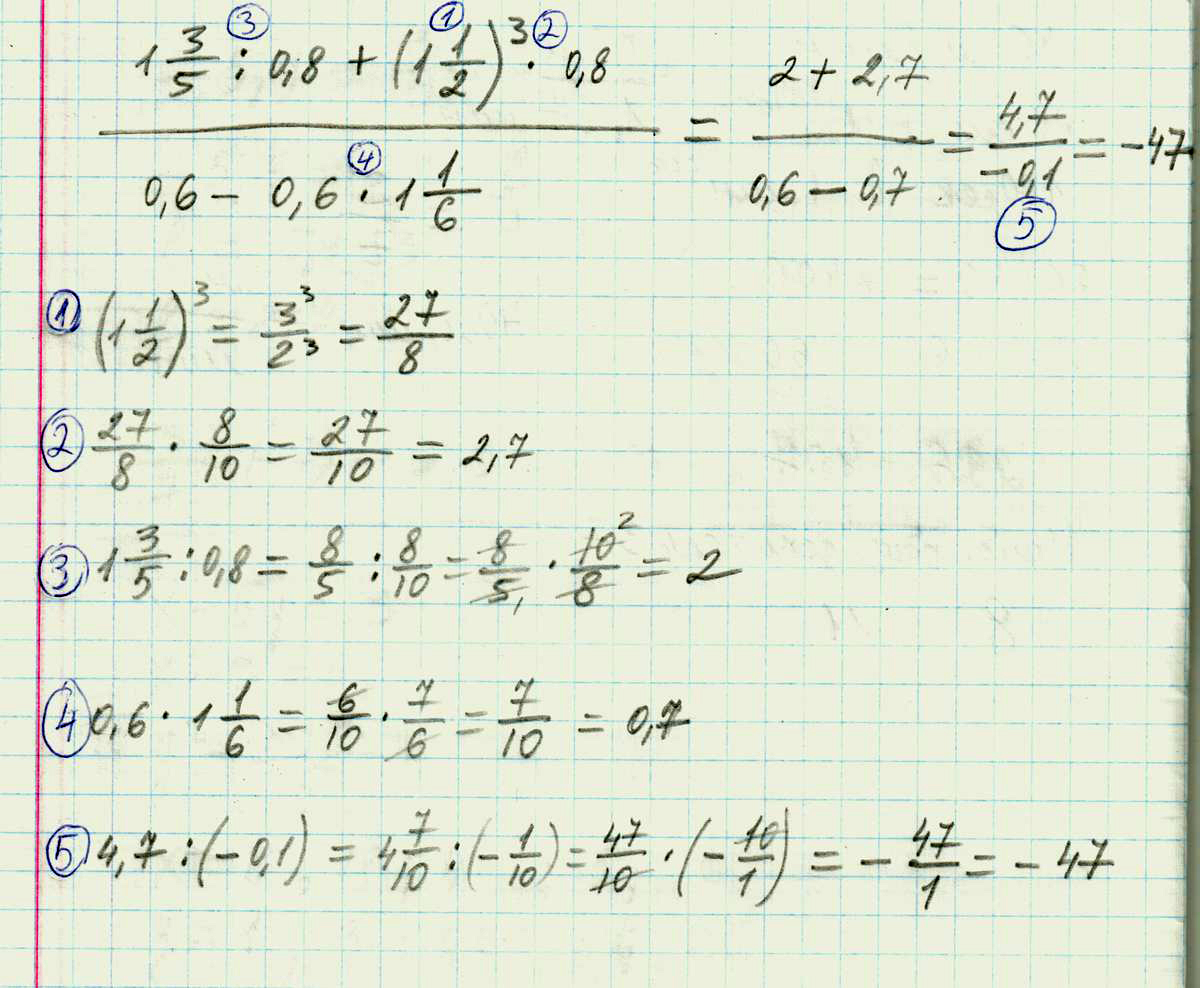
Числитель дроби на 3 больше знаменателя. Если эту дробь сложить с обратной ей дробью, то получится 29/10. Найдите исходную дробь.
Решение: Пусть х - знаменатель дроби, тогда числитель будет х+з(х+3)/х + х/(х+3) = 29/10
приводим к общему знаменателю:
(2х^2 + 6х + 9)/х(х+3) = 29/10
приводим подобные:
х/(х+3) + 3/х + 1 = 29/10
упрощаем:
х/(х+3) + 3/х - 19/10 = 0
решаем уравнение:
- (9*(х^2 + 3х -10))/(10х(х+3)) = 0
х = -5, х = 2
дробь либо -2/-5, либо 5/2
1) Числитель дроби на 2 меньше знаменателя. Если эту дробь сложить с обратной ей дробью, то получим 74/35. Найдите исходную дробь.
2) Лодка прошла 8 км против теч и 12км по течению реки, затратив на весь путь 2 часа. Скорость течения реки =2км/ч, найдите скорость лодки.
3) В раствор, содержащий 2 литра кислоты, долили 10 л воды. В результате концентрации кислоты в растворе уменьшилось на 10%. Сколько литров воды было в растворе изначально?
Решение: 1.
x - числитель.
х+2 - знаменатель.
x/(x+2)+(x+2)/x=74/35
(x²+(x+2)²)/(x*(x+2))=74/35
35*(x²+x²+4x+4)=74*(x*(x+2)
35(2x²+4x+4)=74x²+148x
70x²+140x+140=74x²+148x
4x²+8x-140=0 I÷4
x²+2x-35=0 D=144 √D=12
x₁=5 х∈
x₂=-7 x∉ так как знаменатель должен быть больше числителя
⇒ знаменатель равен 5+2=7.
Ответ: исходная дробь равна 5/7.
x- скорость лодки
8/(x-2)+12(x+2)=2
8x+16+12x-24=2(x-2)(x+2)
20x-8=2*(x²-4)
20x-8=2x²-8
2x²-20x=0 I÷2
x²-10x=0
x(x-10)=0
x₁=10 x₂=0 x₂∉
Ответ: скорость лодки 10 км/ч.
х - изначальное количество литров воды в растворе. ⇒
x+2 - количество литров раствора
2/(х+2+10)=10%/100
2/(х+12)=0,1
2=0,1х+1,2
0,1х=2-1,2
0,1x=0,8
x=8 (л)
Ответ: в растворе изначально было 8 литров.

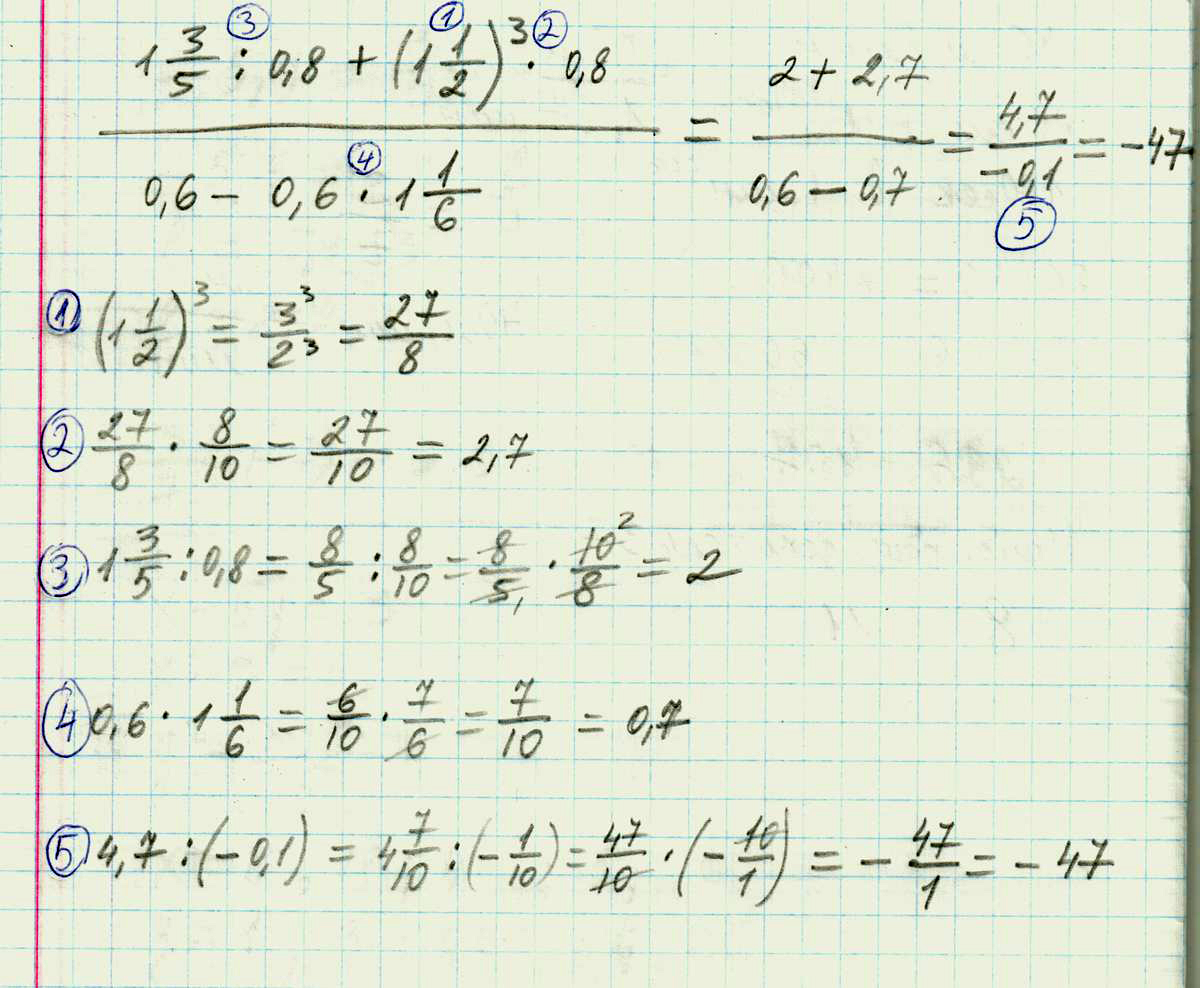
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...