сократите дробь
Сколько целых решений имеет неравенство:sqrt(27-x) >= 7-x
----
Найти произведение xy из системы уравнений:
x-y = 1
81^x-72*9^y = 9
---------
Найти общий вид первообразной функции:
f(x) = 4x^3-1
-----------
Сократите дробь:
(a^9-1)/(a^6+a^3+1)
---------
Решение:
Сколько целых решений имеет неравенство:
sqrt(27-x) >= 7-x
ОДЗ: x <=27
случай 1 x>=7
sqrt(27-x) >=0 >= 7-x
x є { 7;8;9;....;26;27} - целые решения
случай 2 x<7
27-x >= 49+x^2-14x
x^2-13x+22 <= 0
d=169-88=81
x1=(13-9)/2=2
x2=(13+9)/2=11
x є { 2;3;4;5;6} - целые решения
итог x є { 2;3;4;....;26;27} - целые решения - всего 26 целых чисел
ответ 26
----
Найти произведение xy из системы уравнений:
x-y = 1
81^x-72*9^y = 9
*********
x= y+1
81^(y+1)-72*9^y = 9
*********
x= y+1
81*(9^y)^2-72*9^y - 9=0
d=72^2+4*9*81=8100
9^y=(72-90)/(2*81) - лишний корень
9^y=(72+90)/(2*81)=1
y=0
xy=0 - это ответ
---------
Найти общий вид первообразной функции:
f(x) = 4x^3-1
F(x)=x^4-x+c
-----------
Сократите дробь:
(a^9-1)/(a^6+a^3+1)=(a^3-1)
a^3=b
a^6=b^2
a^9=b^3
(a^9-1)/(a^6+a^3+1) = (b^3-1)/(b^2+b^2+1)=b-1=a^3-1
---------1)Найдите абсолютную погрешность округления числа 19,71293 до сотых
2)Сократите дробь а^-13-a-14/a^13-a^14
3) ЗАМЕНИТЕ ДРОБЬ 13/19 ДЕСЯТИЧНОЙ ДРОБЬЮ, ОКРУГЛЕННОЙ ДО ДЕСЯТЫХ, И НАЙДИТЕ АБСОЛЮТНУЮ И ОТНОСИТЕЛЬНУЮ ПОГРЕШНОСТИ ПРИБЛИЖЕНИЯ
Решение: 1)19,71293округляем до сотых: 19,71
Абс. погрешность = |19.71 - 19.71293| = 0.00293
2) $$ \frac{a^{-13}-a^{-14}}{a^{13}-a^{14}} =\\= \frac{\frac{1}{a^{13}}-\frac{1}{a^{14}}}{a^{13}-a^{14}}=\\ = \frac{a-1}{a^{14}}:a^{13}(1-a) =\\= - \frac{1-a}{a^{14}*a^{13}(1-a)} =\\= -\frac{1}{a^{27}} = -a^{-27} $$
3) $$ \frac{13}{19} \approx 0,7 $$
Абс. погрешность = $$ |0.7 - \frac{13}{19}| = |\frac{3}{190}| \approx 0.01579 $$
Отн. погрешность = $$ \frac{3}{190}:\frac{7}{10}*100% = $$ 2.26%
1. Упростить: а) 5√ 3+2√ 27-3√ 12
б) (√45-√20) √5
в) (2√7-3) во второй степени вся скобка
г)(6√3-2√5)(6√3+2√5)
2.Сравнить:
а) 2√7 и 3√6
б)5 целых √две седьмых(дробью) и 2 целых√ семь пятых.
3.Сократить:
а) х во второй степени - 19 б) 29-√29 в) а-6√ав+9в
____________________________ ________ _____________
х+√19 √29 а-9в
4.Освободиться от ирроциональности в знаменателе,избавиться от корня.
а) 2 б) 3
__________ ________
√13 √13-2
5.Вывести множитель из-под знака корня.
а.√6а во второй степени,если "а" меньше или равно нулю.
б.√10в в четвёртой стпени
в.√-"в" в девятой степени
г.√-"а" в пятой степени "в" в десятой степени,если "в" больше нуля.
6.( √в √в ) * √в
_____________ + ___________ _____
√в-√с √с √в-√с
Решение: 1.5√3+2√9*3-3√4*3=5√3+6√3-6√3=5√3
√225-√100=15-10=5
28-12√7+9=37-12√7??
108-20=88
2. <
>
3.(х-√19)(х+√19)
__________________=х-√19
Х+√19
√29(√29-1)
____________=√29-1
√29
(√а-3√в)2
___________________=√@-3√в
(√a-3√в)(√а+3√в) ________
√@+3√в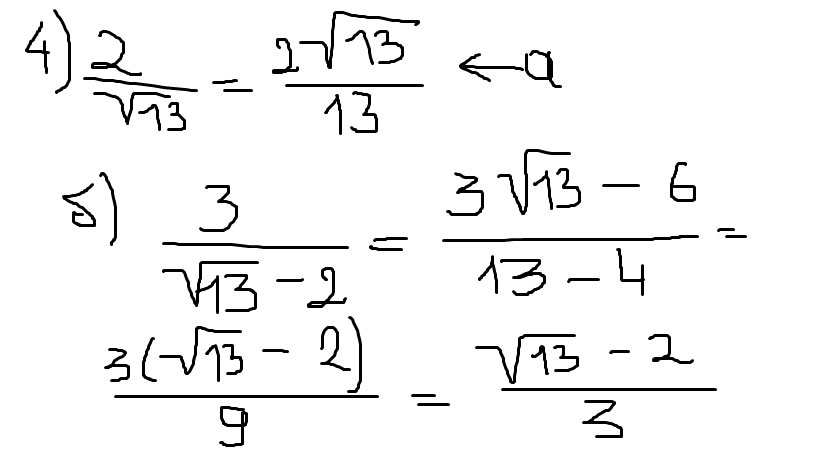
Сократите дробь \( \frac{ab^\frac{1}{2}+b}{a^2-b} \), \( \frac{8a-1}{4a^{\frac{2}{3}}+2\sqrt[3]{a}+1} \)
Решение: $$ a) \frac{ab^\frac{1}{2}+b}{a^2-b} =\frac{b^{\frac{1}{2}}(a+b^{\frac{1}{2}})}{(a-b^{\frac{1}{2}})(a+b^{\frac{1}{2}})}=\frac{b^{\frac{1}{2}}}{a-b^{\frac{1}{2}}}.\\b) \frac{8a-1}{4a^{\frac{2}{3}}+2\sqrt[3]{a}+1}=\frac{2^3a^{\frac{3}{3}}-1}{4a^{\frac{2}{3}}+2a^{\frac{1}{3}}+1}=\\=\frac{(2a^{\frac{1}{3}}-1)(2^2a^{\frac{2}{3}}+2a^{\frac{1}{3}}+1)}{2^2a^{\frac{2}{3}}+2a^{\frac{1}{3}}+1}=2a^{\frac{1}{3}}-1 $$19. Сократите дробь: (5^2 * 100^n)/(2^2n * 5^2n)
20. В треугольнике ABC M - середина AB, N - середина BC, докажите подобие треугольников MBN и ABC
21. На изготовление 20 деталей первый рабочий тратит на один час меньше, чем второй рабочий на изготовление 18 таких же деталей. Известно, что второй рабочий за час делает на 1 деталь меньше, чем первый. Сколько деталей в час делает второй рабочий?
Решение: В решении использованы свойства степеней, признаки подобных треугольников, свойства средней линии треугольника. А в №21 стоит еще определить ОДЗ: х не=0 и х не=-1

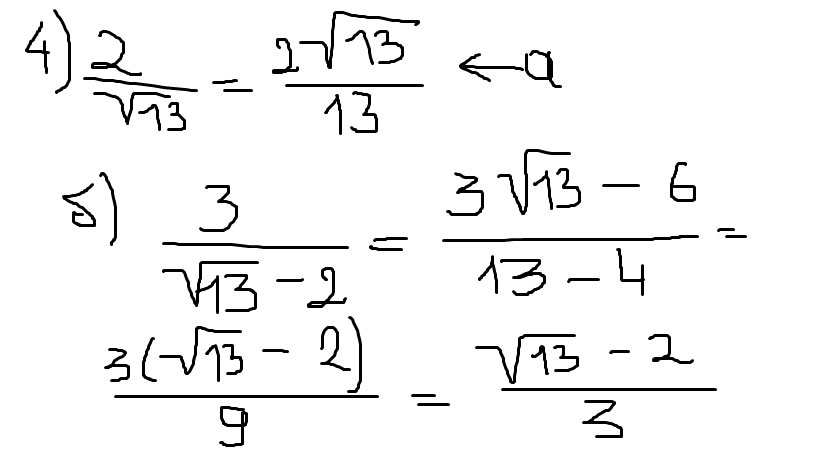

 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...