представить в виде дроби - страница 10
Представьте в виде дроби вырожние пять девятых плюс m n
Решение: 5+9m+9n/дробь/9
Это если m*n.
Если (m+n), то
5+9(m+n)/дробь/95/9 + mn = (5+9mn)/9
Во вложении файл, который показывает, как именно это нужно написать на бумаге.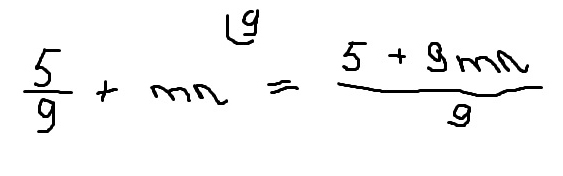
Представьте в виде дроби :
\( \frac{3a}{3a - b} - \frac{a}{3a+b} - \frac{2ab}{9a^{2} - b^{2}} \)
\( \frac{9 - 6x}{x^{3} - 27} + \frac{3- x}{x^{2} + 3x + 9 } \)
Решение: $$ \frac{3a}{3a-b}-\frac{a}{3a+b}-\frac{2ab}{9a^2-b^2} $$Для начала разложим все знаменатели на множители, где можно
$$ \frac{3a}{3a-b}-\frac{a}{3a+b}-\frac{2ab}{(3a-b)(3a+b)} $$
Теперь приводим к общему знаменателю. Общий знаменатель (3a-b)(3a+b)
$$ \frac{3a(3a+b)-a(3a-b)-2ab}{(3a-b)(3a+b)}=\frac{3a^2+3ab-3a^2+ab-2ab}{(3a-b)(3a+b)}=\frac{2ab}{(3a-b)(3a+b)}=\frac{2ab}{9a^2-b^2} \\ \frac{9-6x}{x^3-27}+\frac{3-x}{x^2+3x+9} $$
Опять начинаем решение, с разложения знаменателя на множители.
$$ \frac{9-6x}{(x-3)(x^2+3x+9)}+\frac{3-x}{x^2+3x+9} $$
Приводим к общему знаменателю
$$ \frac{9-6x+(3-x)(x-3)}{(x-3)(x^2+3x+9)}=\frac{x^2-6x}{(x-3)(x^2+3x+9)}=\frac{x^2-6x}{x^3-27} $$
Представить в виде дроби в верху 10 х в квадрате, внизу 2х-3 от этого всего отнять 5х. найти значение при х=0,5
Решение: (10x^2/(2x-3))-5x=? При х=0,5
y=(10x^2/(2x-3))-5x
думаю надо найти производную
у’=(10x^2/(2x-3))’-(5x)’=((10x^2)’(2x-3)-10x^2(2x-3)’)/(2x-3)^2-5
y’=((20x(2x-3)-10x^2*2)/(4x^2-12x+9))-5
y’=((40x^2-60x-20x^2)/(4x^2-12x+9))-5
y’=(20x^2-60x/(4x^2-12x+9))-5 при х=0,5
y’=(20*(0,5)^2-60*0.5/(4*(0.5)^2-12*0.5+9))-5
y’=((20*0,25-3)/(4*0,25-6+9))-5
y’=((5-3)/(1-6+9))-5
y’=2/4-5
y’=0,5-5
y’=-4.5Записать в виде дроби (10 класс)
\(1)\quad \frac{1}{(k-2)!} - \frac{k^3+k}{(k+1)!};\\2)\quad \frac{(n-1)!}{n!} - \frac{n!}{(n +1)!}\)
Решение: $$ 1)\quad \frac{1}{(k-2)!} - \frac{k^3+k}{(k+1)!} = \frac{1}{(k-2)!} - \frac{k(k^2+1)}{(k-2)!\cdot (k-1)\cdot k\cdot (k+1)} =\\\\= \frac{(k-1)\cdot k\cdot (k+1)-k(k^2+1)}{(k-2)!\cdot (k-1)\cdot k\cdot (k+1)} = \frac{ k\cdot (k^2-1-k^2-1)}{k\cdot (k-2)!\cdot (k-1)\cdot (k+1)} =\frac{-2}{(k-2)!\cdot (k^2-1)} \\ 2)\quad \frac{(n-1)!}{n!} - \frac{n!}{(n +1)!} = \frac{(n-1)!}{(n-1)!\cdot n} - \frac{n!}{n!\cdot (n+1)} =\frac{1}{n}-\frac{1}{n+1}=\\\\=\frac{n+1-n}{n\cdot (n+1)}=\frac{1}{n\cdot (n+1)} $$Представить в виде дроби \(\frac{1}{(x-2)(x-1)}+\frac{1}{(x-1)x}+\frac{1}{x(x+1)}+\frac{1}{(x+1)(x+2)}\)
Решение: $$ \frac{1}{(x-2)(x-1)}+\frac{1}{(x-1)x}+\frac{1}{x(x+1)}+\frac{1}{(x+1)(x+2)}=\\\\=\frac{1}{x-1}(\frac{1}{x-2}+\frac{1}{x})+\frac{1}{x+1}(\frac{1}{x}+\frac{1}{x+2})=\\\\=\frac{1}{x-1}\cdot\frac{x+x-2}{x(x-2)}+\frac{1}{x+1}\cdot\frac{x+2+x}{x(x+2)}=\\\\=\frac{1}{x-1}\cdot\frac{2x-2}{x(x-2)}+\frac{1}{x+1}\cdot\frac{2x+2}{x(x+2)}=\\\\=\frac{2(x-1)}{x(x-1)(x-2)}+\frac{2(x+1)}{x(x+1)(x+2)}=\frac{2}{x(x-2)}+\frac{2}{x(x+2)}=\\\\=\frac{2(x+2)+2(x-2)}{x(x-2)(x+2)}=\frac{2x+4+2x-4}{x(x-2)(x+2)}=\frac{4x}{x(x^2-2^2)}= \\ =\frac{4}{x^2-4}. $$Общий знаменатель = (х - 2) * (х - 1) * (х + 1) * (х + 2) * х
( (х + 1) * (х + 2) * х + (х - 2) * (х + 1) * (х + 2) * х + (х - 2) * (х - 1) * (х + 2) + (х - 2) * (х - 1) * х )/(х^2 - 4) * (х^2 - 1) * х
( (х^2 + 2х + х + 2) * х + (х^2 + 4) * (х + 1) * х + (х^2 - 4) * (х - 1) + (х^2 - х - 2х + 2) * х )/(х^2 - 4) * (х^2 - 1) * х
( х^3 + 2х^2 + х^2 + 2х + (х^3 + х^2 + 4х + 4) * х + х^3 - х^2 - 4х + 4 + х^3 - х^2 - 2х^2 + 2х )/(х^2 - 4) * ( х^2 - 1) * х
( х^3 + 2х^2 + х^2 + 2х + х^4 + х^3 + 4х^2 + 4х + х^3 - х^2 - 4х + 4 + х^3 - х^2 - 2х^2 + 2х )/(х^2 - 4) * ( х^2 - 1) * х
Сейчас в числителе приводим подобные
( х^4 + 4х^3 + 3х^2 + 4х + 4)/(х^4 - х^2 - 4х^2 + 4) * х
( х^4 + 4х^3 + 3х^2 + 4х + 4)/х^5 - х^3 - 4х^3 + 4х
( х^4 + 4х^3 + 3х^2 + 4х + 4)/х^5 - 5х^3 + 4х

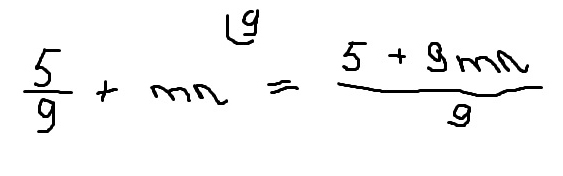
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...