натуральные числа

Найдите наибольшее натуральное число, которые есть решением неравенства (x^2-10x+25)(x+3)^9(4-x)>=0

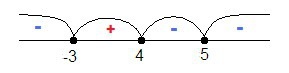
Назовем натуральное число n-богатым,если сумма всех его натуральных делителей больше 2n.например ,12 -число богатое,т.к.1+2+3+4+6+12 больше 24.Каким неможет быть богатое число?
А)точным квадратом
Б)числом,кратным 2013
В)больше миллиона
г)степень. числа 3
д)каждое из свойств А-Г -возможно.

     n^2+n+1 >= n + n + 1 > n

г) 3^n

    3 + 3^2 + ... + 3^n = 3(1+3+...+3^n-1) = 3*(3^n -1)/(3-1) = 3/2*3^n - 3/2 < 2*3^n

Из того, что необходимо выбрать один вариант, и вариант д) оказался невозможным в силу того, что в варианте г) степень числа трех не может быть n-богатым, остаётся г)

Вариант г)

1) Я задумал некоторое натуральное число. Затем я умножил предшествующее ему число на следующие за задуманным и получил 168, какое число я задумал.
2)преобразуй выражение в многочлен:
(0,6-у)в 2 степени
(-2-n)в 2 степени
(а в 2 степени/5 (а пятых)-15b)в 2 степени.
3)представь произведение в виде многочлена:
(А-8)(А+8)
(3в в 2 степени+5а)(5а-3в в 2 степени)
4)Является ли данный многочлен стандартного вида кубом двучлена?
в в 3 степени -6 в в 2 степени +12в -8
27х в 3 степени-108х в 2 степени у+144ху в 2 степени-64 у в 3 степени 5) упростите выражение: (в-2а)в 2 степени -(2в+а)(2в-а)

(х-1) предшествующее число

(х+1) следующее число

(х-1)(х+1)=168

х²-1=168

х²=169

х=13 задуманное число

2)преобразуй выражение в многочлен:
(0,6-у)²=0,36-1,2y+y²
(-2-n)²=4+4n+n²
(а²/5-15b)²=a⁴/25-6a²b+225b²

3)представь произведение в виде многочлена:
(А-8)(А+8)=a²-64
(3в²+5а)(5а-3в²)=25a²-9b⁴

4)Является ли данный многочлен стандартного вида кубом двучлена?
в³-6в² +12в -8=b³-3*b²*2+3*b*2²-2³=(b-2)³
27х³-108х²у+144ху²-64 у³=(3x)³-3*9x²*4y+3*3x*16y²-(4y)²=(3x-4y)³
5)упростите выражение:
(в-2а)² -(2в+а)(2в-а)=b²-4ab+4a²-4b²+a²=5a²-4ab-3b²

Доказать, что если натуральное число при делении на 4 дает в остатке 2, то это число четное. У к а з а н и е. Рассматриваемое число представить в виде4n+2, где n- частное от деления этого числа на 4. Натуральное число а при делении на 3 дает в остатке 1, а натуральное число b при делении на 3 дает в остатке 2. Доказать, что сумма чисел a и b кратка трем. Доказать, что сумма двух последовательных четных степеней числа 3 оканчивается нулем. Доказать, что это же справедливо и для суммы двух последовательных нечетных степеней числа 3.

2)Из условия следует что a=3n+1, а b=3k+2. Их сумма=3n+1+3k+2=3n+3k+3=3(n+k+1), значит их сумма кратна 3

3)все четные числа представляются в виде 2n. Нам нужно доказать что $$ 3^{2n}+3^{2(n+1)} $$ оканчивается на 0, то есть делится на 10.

Но$$ 3^{2n}+3^{2(n+1)}=9^n+9^{n+1}=9^n(1+9)=9^n*10 $$

4)все нечетные числа представляются в виде 2n+1. Нам нужно доказать что оканчивается на 0, то есть делится на 10.

Но

$$ 3^{2n+1}+3^{2(n+1)+1}=3^{2n+1}+3^{2n+3}=3^{2n+1}(1+3^2)= $$

$$ =10*3^{2n+1} $$

Докажите,что число (√2-1)в сотой степени можно представить в виде √m+1-√m,где m натуральное число.

Если в числе $$ ( \sqrt{2} -1)^{100} $$  раскрыть 100-ую степень по биному Ньютона, то получится сумма слагаемых вида  $$ C_{100}^k(\sqrt{2})^{k}(-1)^{100-k} $$ по k от 0 до 100. При четных k эти слагаемые будут натуральными числами, а при нечетных k они имеют вид $$ -a\sqrt{2} $$, где а - натуральное. Значит, $$ ( \sqrt{2} -1)^{100}=A-B\sqrt{2} $$, при некоторых натуральных $$ A $$ и $$ B $$. (для решения задачи нет нужды их явно вычислять). Опять же из бинома Ньютона понятно, что тогда $$ ( \sqrt{2} +1)^{100}=A+B\sqrt{2} $$, т.к. в нем будут те же слагаемые, только все со знаком плюс. Перемножив эти два соотношения, получим $$ A^2-2B^2=(A-B\sqrt{2})(A+B\sqrt{2})=(\sqrt{2}-1)^{100}(\sqrt{2}+1)^{100}=1 $$, то есть $$ A^2=2B^2+1 $$. Поэтому, если положим \( m=2B^2 \), то получим, что \( \sqrt{m+1}-\sqrt{m}=\sqrt{2B^2+1}-\sqrt{2B^2}=\sqrt{A^2}-\sqrt{2B^2}=\\=A-B\sqrt{2}=( \sqrt{2} -1)^{100}.\)