натуральные числа - страница 5
1) Сформулируйте правило умножения?
2) Как умножит смешанные числа?
3) Какие числа называют взаимно обратными?
3) Сформулируйте правило деления обыкновенных дробей?
5) Как разделить дробь на натуральное число?
Натуралное число на дробь?
6) Как найти дробь от числа?
7) Как найти число по известной дроби?
8) Как найти несколько процентов от числа?
9) Как найти число, если известны его проценты?
10) Приведите пример бесконечной периодической десятичной дроби?
11) Как можно получить число 0,6666.
12) Как обыкновенные дроби преобразовать в десятичные?
13) Сформулируйте правила сложения и вычитания приближенных значений?
Решение: 1) -2) сначала нужно перевести числа в неправильную дробь, а затем перемножить числители и знаменатели.
3) взаимно обратные числа это те. которые при умножении друг на друга дают единицу (5*1/5(пять умножить на одну пятую))
3) чтобы разделить дробь на дробь, нужно заменить деление умножением, т. е. перевернуть делитель знаменателем наверх, и перемножить дроби
5) чтобы разделить натуральное число на дробь нужно превернуть дробь (заменить деление умножением) и перемножить числитель с натуральным числом.
чтобы разделить дробь на натуральное число, нужно (заменить деление умножением) т. е. перевернуть дробь и перемножить числитель и натуральное число.
6) чтобы найти дробь от числа, нужно умножить число на эту дробь. или умножить на числитель и разделить на знаменатель
7) чтобы найти число по известной дроби, нужно разделить число на эту дробь. или разделить на числитель и умножить на знаменатель
8) нужно разделить число процентов на 100 (к примеру 34% = 0,34) и это число умножить на кол-во процентов (например 67*0,34)
9) разделить на процент. (см. ответ выше)
10) 1:3 = 0,9999.
11) -
12) разделить числитель на знаменатель
Деление десятичной дроби на натуральное число в столбик
13,68 : 6 | 2,304 : 3 | 0,27 : 9 | 18,15 : 6
Решение: Умножай оба числа на кол-во знаков после запятой и дели как обычно:
13,68:6 это тоже самое что и 1368 : 600 и т. д.6 3 9
1 3,6 8 ! 2,3 0 4 ! 0, 2 7 !
1 2 2,28 2 1 0,768 2 7 0,03
-
1 6 2 0 0
1 2 1 8
-
4 8 2 4
4 8 2 4
-
0 0
6
1 8,1 5 !
1 8 3,025
-
1 5
1 2
-
3 0
3 0
-
0Деление десятичной дроби на двузначное натуральное число (десятитысячные)
Выполни деление.
0,1104 : 69 =
Решение: 0.0016.
.0,1104=1104/10000 Когда мы делим на дробь, эта дробь переворачивается и получается 100/69 Затем сокращаем крест на крест
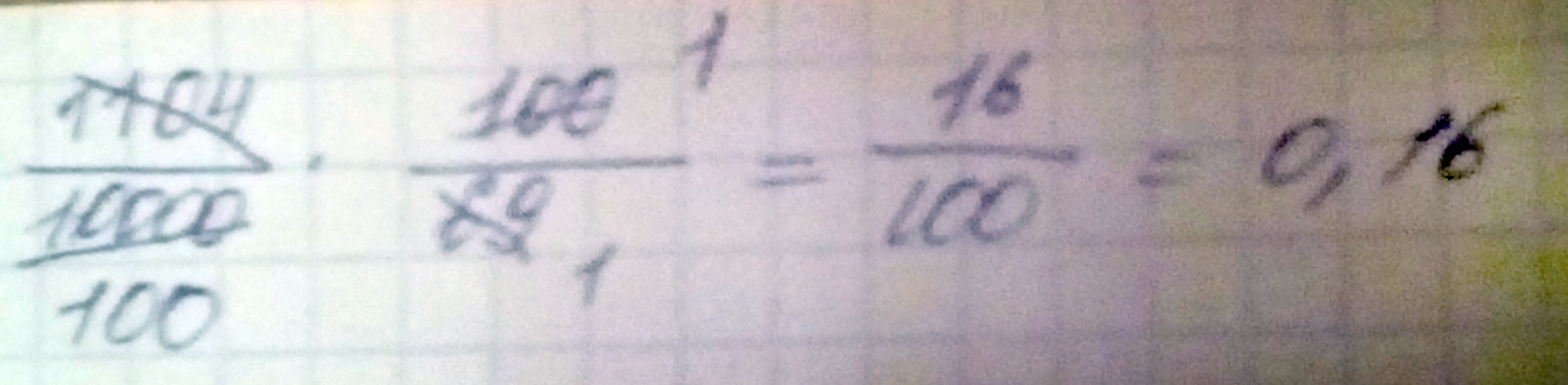
Напишите пж ДЛЯ УСТНОГО СЧЕТА примеры 5 на деление десятичной дроби на натуральное число и 5 на деление десятичной дроби на десятичную.
Решение: 0,2 поділити на 10 0,8 поділити на 2 0,27 поділити на 3 0,6 поділити на 12 0,1 поділити на 2Хотя бы не всё
Вопросы к теоретическому зачету в 5 классе:
1. Определение натурального числа.
2. Определение отрезка.
3. Правила округления натурального числа и десятичной дроби.
4. Переместительный и сочетательный законы сложения и умножения (правила и формула).
5. Распределительный закон умножения относительно сложения и вычитания (правила и формула).
6. Определение уравнения, корня уравнения.
7. Что значит, решить уравнение?
8. Определение подобных слагаемых.
9. Правило сложения и вычитания подобных слагаемых.
10. Формула деления с остатком.
11. Правила сравнения дробей.
12. Правила нахождения дроби от числа и целого по его части.
13. Основное свойство дроби.
14. Определения окружности, радиуса, хорды, диаметра, круга.
15. Правила сложения и вычитания дробей с одинаковыми знаменателями.
16. Правило умножения дроби на натуральное число.
17. Правило деления дроби на натуральное число.
18. Определения угла, противоположных лучей, развернутого угла, биссектрисы угла, треугольника.
19. Неравенство треугольника.
20. Определение катетов и гипотенузы.
21. Правила нахождения площади прямоугольного треугольника и произвольного треугольника.
22. Определение высоты треугольника.
23. Определение равнобедренного треугольника (боковые стороны, основание).
24. Свойство углов равнобедренного треугольника.
25. Свойство углов равностороннего треугольника.
26. Определение перпендикулярных прямых.
27. Определение перпендикуляра.
28. Определение срединного перпендикуляра.
29. Основное свойство срединного перпендикуляра.
30. Определение расстояния от точки до прямой.
31. Основное свойство биссектрисы угла.
Решение: 1. Числа, используемые при счёте.2. Часть отрезка, ограниченная двумя точками.
4. Переместительный (коммутативный) закон сложения: m + n = n + m. Сумма не меняется от перестановки её слагаемых.
Переместительный (коммутативный) закон умножения: m · n = n · m. Произведение не меняется от перестановки его сомножителей.
Сочетательный (ассоциативный) закон сложения: ( m + n ) + k = m + ( n + k ) = m + n + k. Сумма не зависит от группировки её слагаемых.
Сочетательный (ассоциативный) закон умножения: ( m · n ) · k = m · ( n · k ) = m · n · k. Произведение не зависит от группировки его сомножителей.Распределительный (дистрибутивный) закон умножения относительно сложения: ( m + n ) · k = m · k + n · k.
5. (a+b)*c=a*c+b*c
6. Уравнение – это равенство, содержащее одну или несколько переменных.
7. Вычислить значение перемннной.
11. Приводим к одному знаменателю. У какой дроби числитель больше числителя другой дроби, та и больше.
15. Работаем с числителями.

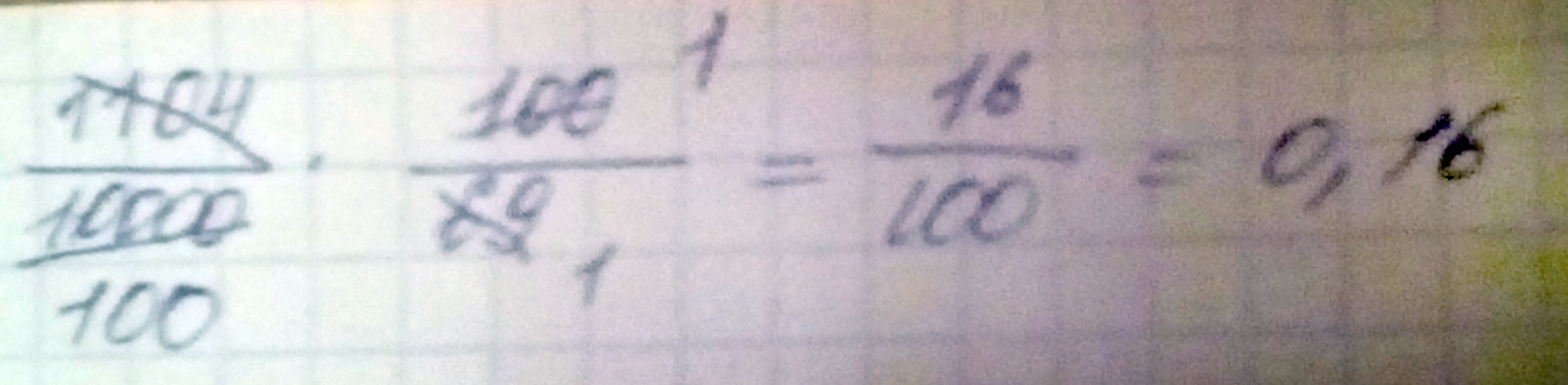
 Если ограничиваться только вещественными числами, то, как известно, действие извлечения корня не всегда выполнимо; корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. В связи с этим уже квадратное уравнение с вещественными коэффициентами не всегда имеет вещественные корни.Это обстоятельство приводит, естественно к расширению понятия о числе, к введению новых чисел более общей природы, частным случаем...
Если ограничиваться только вещественными числами, то, как известно, действие извлечения корня не всегда выполнимо; корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. В связи с этим уже квадратное уравнение с вещественными коэффициентами не всегда имеет вещественные корни.Это обстоятельство приводит, естественно к расширению понятия о числе, к введению новых чисел более общей природы, частным случаем...