натуральные числа - страница 4
1) Я задумал некоторое натуральное число. Затем я умножил предшествующее ему число на следующие за задуманным и получил 168, какое число я задумал.
2) преобразуй выражение в многочлен:
(0,6-у) в 2 степени
(-2-n) в 2 степени
(а в 2 степени/5 (а пятых)-15b) в 2 степени.
3) представь произведение в виде многочлена:
(А-8)(А+8)
(3в в 2 степени+5а)(5а-3в в 2 степени)
4) Является ли данный многочлен стандартного вида кубом двучлена?
в в 3 степени -6 в в 2 степени +12в -8
27х в 3 степени-108х в 2 степени у+144ху в 2 степени-64 у в 3 степени
5) упростите выражение:
(в-2а) в 2 степени -(2в+а)(2в-а)
Решение: 1) х задуманное число(х-1) предшествующее число
(х+1) следующее число
(х-1)(х+1)=168
х²-1=168
х²=169
х=13 задуманное число
2) преобразуй выражение в многочлен:
(0,6-у)²=0,36-1,2y+y²
(-2-n)²=4+4n+n²
(а²/5-15b)²=a⁴/25-6a²b+225b²3) представь произведение в виде многочлена:
(А-8)(А+8)=a²-64
(3в²+5а)(5а-3в²)=25a²-9b⁴4) Является ли данный многочлен стандартного вида кубом двучлена?
в³-6в² +12в -8=b³-3*b²*2+3*b*2²-2³=(b-2)³
27х³-108х²у+144ху²-64 у³=(3x)³-3*9x²*4y+3*3x*16y²-(4y)²=(3x-4y)³
5) упростите выражение:
(в-2а)² -(2в+а)(2в-а)=b²-4ab+4a²-4b²+a²=5a²-4ab-3b²Деление десятичных дробей (сотые)
Замени деление на натуральное число и вычисли.
0,2:0,05=
Решение: вот решение 0,2=2/10 0,05=5/100 При делении дробь на которую делим переворачивается, соответственно получается 100/5 Затем сокращаем крест на крест, получаем 20/5=4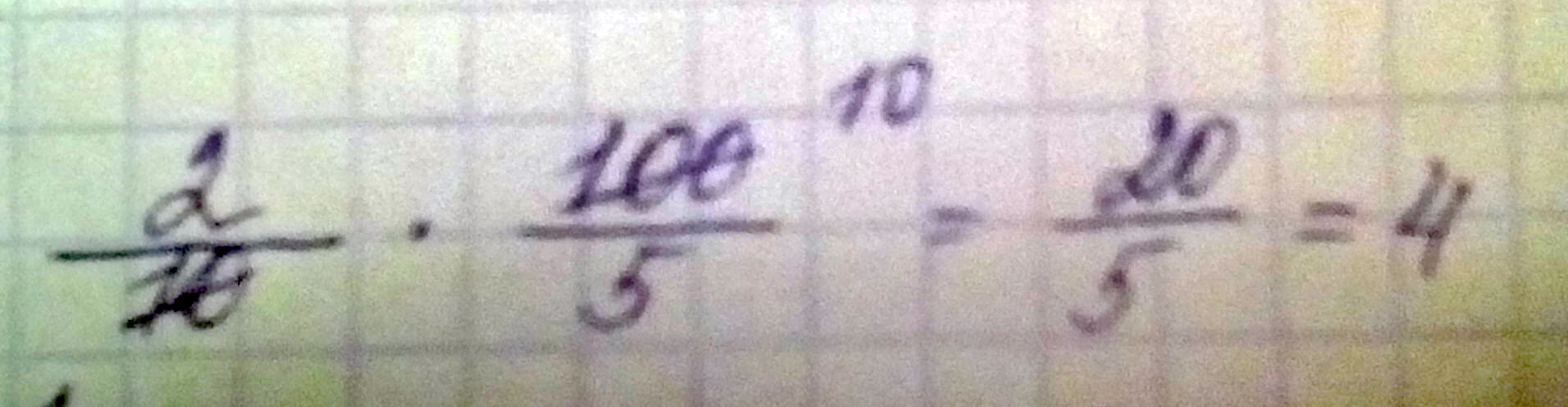
1. Сложение обыкновенных дробей с одинаковым знаменателем.
2. Сложение обыкновенных дробей с разным знаменателем.
3. Вычитание обыкновенных дробей с одинаковым знаменателем.
4. Вычитание обыкновенных дробей с разным знаменателем.
5. Отыскание части от целого и целого по его части.
6. Основное свойство дроби.
7. Сложение и вычитание смешанных чисел.
8. Умножение обыкновенной дроби на натуральное число.
9. Деление обыкновенной дроби на натуральное число.
10. Умножение и деление десятичной дроби на 10,100,1000 и т. д.
11. Сложение и вычитание десятичных дробей.
12. Умножение десятичных дробей.
13. Деление десятичных дробей.
14. Среднее арифметическое.
15. Нахождение процента от числа.
16. Нахождение числа по его проценту.
Решение: 1) складываете числители и получаете результат. знаменатель тот же
1/4+3/4=4/4
2) находите общий знаменатель. домножаете. складываете.
1/2+1/4=2/4+1/4=3/4
3) вычитаете числители.
3/4-2/4=1/4
4) общий знаменатель. домножаем. вычитаем.
1/2-1/4=2/4-1/4=1/4
7) переводим в неправильную дробь. общий знаменатель. выполняем действие.
1 1/2 +1 3/4=3/2+7/4=6/4+7/4=13/4=3 1/4
14) складываем все числа и делим на их количество
(2+4+6)/3=4 среднее арифметическое1. складываем числители, а знаменатель остается тот же
2. привести дроби к наименьшему ОБЩЕМУ знаменателю.(числитель и знаменатель каждой дроби умножаем на нужный множительт)
3. вычитаем из большего числителя меньший, знаменатель остается
4. приводим к общему знаменателю и из большего числителя вычитаем.
5. если находим число по части, то делим число на эту дробь (на эту часть)
чтобы найти часть от числа, умножаем число на дробь
6. Если числитель и знаменатель этой дроби мы умножим или разделим на одно и то же число (не 0), то величина дроби не изменится.
7. приводим к общему знаменателю, складываем или вычитаем целые числа, потом дробные, которые приведены к общему знаменателю.
8. умножаем на натуральное число числитель, знаменатель оставляем как был
9. знаменатель умножаем на натуральное число, числитель остается тот же
10. умножение: переносим запятую вправо на столько, сколько нулей. деление: переносим влево.
11. приравняем числа, то есть после запятой нужно, чтобы было одинаковое количество цифр, если их не хватает добавляем нули. И складываем и вычитаем как обычно
12. умножаем не смотря на запятые, потом в ответе отсчитаем место где поставить запятую, отделяя столько знаков сколько в двух десятичных дробях.
13. при делении: делим и не смотрим на запятую, если закончится деление целой части, то ставим запятую.
14. складываем все данные числа и делим результат на количество сложенных чисел
15. число умножаем на данный процент и делим на 100
15. число разделить на % и умножить на 1001 задание. Какую дробь называют десятичной? Приведите примеры таких дробей и назовите по порядку первые четыре разряда, стоящие в десятичной дроби справа от запятой. Изменится ли десятичная дробь, если к ней справа приписать один или несколько нулей? Как представить обыкновенную дробь в виде десятичной ? Приведите пример.
2 задание. По какому правилу выполняется:
а) сложение (вычитание обыкновенных дробей с одинаковыми знаменателями.
б) сложение (вычитание ) десятичных дробей.
в) умножение десятичных дробей.
г) умножение десятичной дроби на 10, 100, 1000 и т. д
д) деление десятичной дроби на натуральное число.
е) деление числа на десятичную дробь.
ж) умножение десятичной дроби на 0,1 ; 0,01 ; 0, 001 и т. д
з) деление десятичной дроби на 10, 100, 1000 и т. д
и) деление десятичной дроби на 0,1 ; 0,01 ; 0,001 и т. д.
вас, , .
Решение: Задание 1
1. Десятичной дробью называют обыкновенную дробь, знаменателем которой является единица с последующими нулями или же десятичная дробь есть результат деления единицы на десять, сто, тысячу и т. д. частей.
Прим.: 1,3; 25,96 ; 1,203 и т. д
Разряды после запятой по порядку: десятки, сотни, тысячи, десятки тысяч
Основное свойство десятичной дроби
Свойство: Если к десятичной дроби справа дописать несколько нулей, то величина десятичной дроби не изменится.
Чтобы представить обыкновенную дробь в виде десятичной, просто выполните деление - разделите числитель данной дроби на знаменатель. прим 2/4=0,5
Задание 2
а) чтобы сложить(вычесть) 2 дроби с одинаковыми знаменателями, нужно просто сложить(вычесть) числитель первой дроби с(из) числителем второй дроби, а знаменатель оставить тот же.
б) сложение (вычитание ) десятичных дробей проводится по разрядам, десятки складываются с десятками, единицы с единицами, запятая сохраняет свое место, число после запятой так же складываются по разрядам.
в) Умножение двух десятичных дробей выполняется так:
1) числа перемножаются без учета запятых.
2) запятая в произведении ставится так, чтобы отделить справа
столько же знаков, сколько отделено в обоих множителях
вместе взятых.
г) При умножении десятичной дроби на 10, 100, 1000 и т. д. надо
в этой дроби перенести запятую вправо на столько знаков, сколько нулей
стоит в множителе.
д) Чтобы разделить десятичную дробь на натуральное число, надо:
1) разделить дробь на это число, не обращая внимания на запятую;
2) поставить в частном запятую, когда кончится деление целой части.
е) При делении на десятичную дробь, сначала переносим запятую в делимом и делителе вправо на столько знаков, сколько их после запятой в делителе. А затем выполняем деление на натуральное число.
ж) Вместо умножения любого числа на 0,1 ; 0,01 ; 0,001,
можно разделить это число на 10 ; 100 ; или 1000 соответственно.
з) при делении десятичной дроби на 10,100 и тд, нужно просто переместить запятую настолько знаков влево, сколько нулей в делителе( 10 значит на 1 знак)
и) деление десятичной дроби на 0,1 ; 0,01 ; 0,001 и т. д нужно перенести запятуна на столько знаков вправо, сколько чисел после запятой делителя№ Теория к зачету по десятичным дробям
1 Как короче записывают дроби, знаменатель которых единица с несколькими нулями?
2 Сколько цифр будет стоять после запятой в десятичной записи дроби 18 ?
3 Какое число будет в этой записи после запятой и какое до запятой?
4 Как складывают и как вычитают десятичные дроби?
5 Назовите первые три разряда после запятой в десятичных дробях.
6 Как сравнивают десятичные дроби по разрядам ?
7 Сформулируйте правило округления чисел.
8 Сформулируйте правило умножения десятичной дроби на натуральное число.
9 Как умножить десятичную дробь на 10; на 100; на 1000?
10 Как делят десятичную дробь на натуральное число?
11 Как разделить десятичную дробь на 10, 100, 1000?
12 Как обратить обыкновенную дробь в десятичную?
13 Как умножить десятичную дробь на 0,1; 0,01; 0,001?
14 Сформулируйте правило умножения на десятичную дробь.
15 Сформулируйте правило деления десятичной дроби: на десятичную дробь; на 0,1; 0,01; 0,001.
Решение: 1. обыкновенную в форме десятичной
2. лучше допиши вопрос 18 это целое число
3.
4. Дробь не изменится, потому что произойдёт сокращение дроби
5. единицы десятки сотые тысячные
6. Сравнение дробной части десятичной дроби производится по разрядам от меньшего к большему разряду. Та десятичная дробь больше (меньше), у которой величина числа в разряде больше (меньше).
7. Чтобы округлить десятичную дробь до определенного разряда целой или дробной части, все меньшие разряды заменяются нулями или отбрасываются, а предшествующий отбрасываемой при округлении цифре разряд не изменяет своей величины, если за ним идут цифры 0, 1, 2, 3, 4, и увеличивается на 1 (единицу), если идут цифры 5, 6, 7, 8, 9.
8. Умножение десятичных дробей производится так же, как и умножение натуральных чисел, по тем же правилам, но в произведении ставится запятая по сумме разрядов множителей в дробной части, считая справа налево (сумма разрядов множителей — это количество разрядов после запятой у множителей, вместе взятых).
9. нужно в этой дроби перенести запятую на столько цифр вправо, сколько нулей содержится в множителе.
10. разделить дробь на это число, не обращая внимания на запятую, поставить в частном запятую, когда закончится деление целой части
11. надо перенести запятую в этой дроби влево на столько знаков,
сколько нулей в делителе
12. надо разделить числитель на знаменатель в соответствии с правилами деления
13. в множимом перенести запятую на столько знаков сколько их после запятой во множителе
14.
15. надо перенести в ней запятую на столько цифр вправо, сколько стоит нулей перед единицей в делителе (или умножить делимое и делитель на 10, 100, 1000и т. д.).

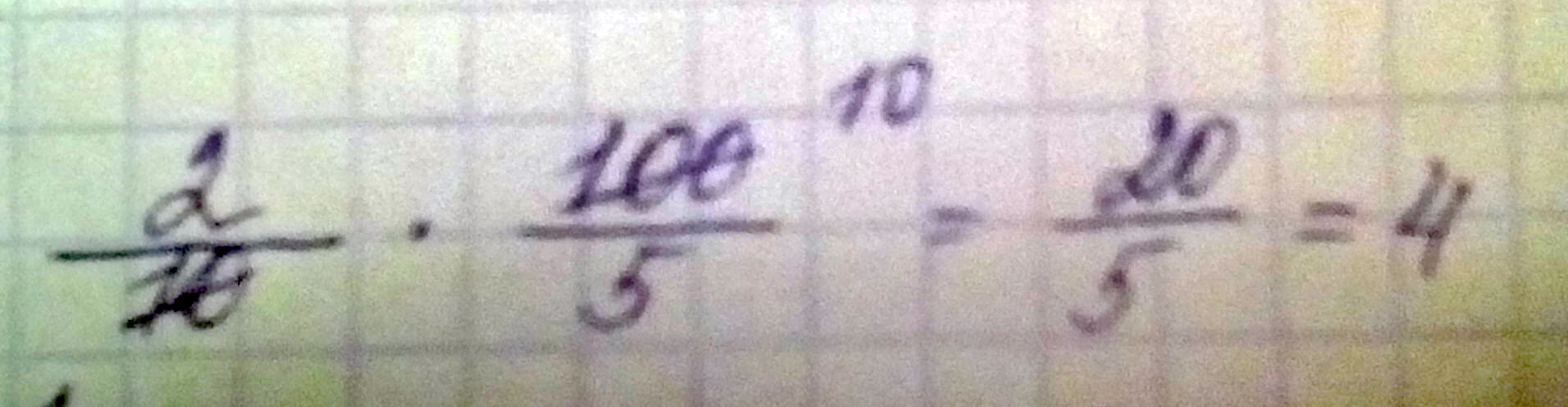
 Если ограничиваться только вещественными числами, то, как известно, действие извлечения корня не всегда выполнимо; корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. В связи с этим уже квадратное уравнение с вещественными коэффициентами не всегда имеет вещественные корни.Это обстоятельство приводит, естественно к расширению понятия о числе, к введению новых чисел более общей природы, частным случаем...
Если ограничиваться только вещественными числами, то, как известно, действие извлечения корня не всегда выполнимо; корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. В связи с этим уже квадратное уравнение с вещественными коэффициентами не всегда имеет вещественные корни.Это обстоятельство приводит, естественно к расширению понятия о числе, к введению новых чисел более общей природы, частным случаем...