иррациональное число
1) Найдите сумму наибольшего и наименьшего значения функции \( f(x)=3^{x}+3^{2-x} \) на отрезке \( \left[\begin{array}{ccc}-1;2\end{array}\right] \)
2) Вычислите интеграл: \( \int\limits^4_1 {\frac{5\sqrt{x}}{x}} \, dx \)
3) Исключите иррациональность в знаменателе \( \frac{12}{3+\sqrt{2}-\sqrt{3}} \)
Решение: см. влож===========================================
6*(3+sqrt(2)+sqrt(3))/(4+3sqrt(2))=6*(3+sqrt(2)+sqrt(3))*(4-3sqrt(2))/(16-18)=
=3(3sqrt(2)-4)(3+sqrt(3)+sqrt(2))=3(5sqrt(2)-6-4sqrt(3)+3sqrt(6))
F(x)=5*sqrt(x)*2
F(4)=20
F(1)=10
F(4)-F(1)=10
f’(x)=3^xln3-9*3^(-x)*ln3
3^x-93^(-x)=0
x=1
f(1)=3+3=6
f(-1)=1/3+3^3=27 1/3
F(2)=9+1=10
6+27 1/3=33 1/3
ответ 33 1/3
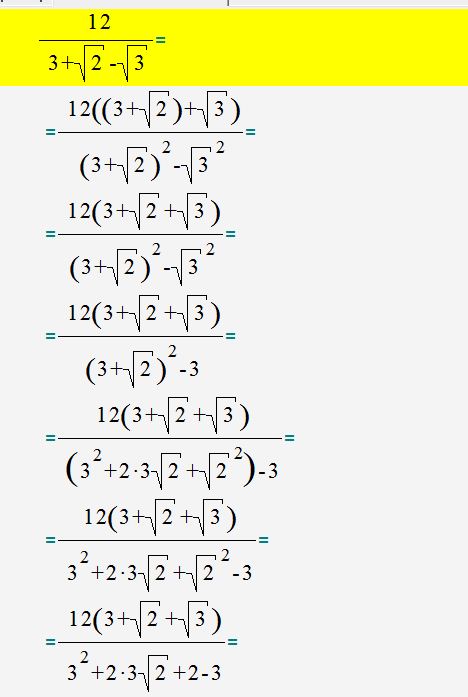
Число 0,09 ( с периодом над 09 ) это рациональное или иррациональное число?
Решение: Иррациональное, т. к. Действительные числа - это числа вида m/n, где m-целое число, n-натуральное.
Иррациональное число - это число, не являющееся рациональным, то есть такое, которое нельзя представить в виде отношения двух целых чисел.
Рациональные числа, если их записать десятичной дробью, обязательно дадут конечную или бесконечную периодическую дробь. Это тоже легко доказать. Иррациональные же числа, записанные в виде десятичной дроби, оказываются представленными бесконечной НЕпериодической дробью.
Типичным примером иррационального числа является корень квадратный из двух. Пи - тоже иррациональное число, причем в определенном смысле более сложное, чем корень из двух, потому что Пи нельзя представить в виде корня из рационального числа.
Как проще понять, что такое иррациональное число, рациональное ?
Решение: Иррациональное не выносится из под корня, например √15, а рациональное можно вынести, например √36 = 6Все целые и дробные числа называют рациональными каждое рационально число может быть представлено в виде бесконечной десятичной периодической дроби например 2,5=2,500000
1) Число а -рациональное, а число b-иррациональное. Каким числом, рациональным или иррациональным, является:
а) 3а+b
б) а+2b
в) а2+4а+b
г) 3а2-а+4b?
2) При каких значениях а и b прямые у=-2х+b и у=ах-b пересекаются в точке (3;-1)?
Решение: В первом задании все числа будут иррациональные, т. к. чтобы избавиться от иррациональности, нужно возвести b в квадрат, таких операций нет, значит, все иррациональные. Во втором мы подставляем вместо x и y числа, находим b : $$ \left \{ {{-1=-2*3+b} \atop {-1=3*a-b}} \right.; +\left \{ {{-1=-6+b} \atop {-1=3a-b}} \right.; -2=3a-6;3a=4;a= \frac{4}{3}; -1=4-b; $$, b=5Как определить какое число рациональное или иррациональное
Решение: Иррациональное число - это число, которе не имеет точного значения
Например sqrt(2).Рациональные числа - те числа, которые можно представить в виде периодической десятичной дроби. Т. е. такой дроби, у которой числа после запятой повторяются. 1,(3)=1,333333.
В виде периодической дроби можно представить любое целое и дробное число. 2=2,(0). 1/3=0,(3)
Но есть числа, которые нельзя представить в виде периодической дроби. У них бесконечное количество цифр после запятой, они не повторяются. Это иррациональные числа.
Пример иррациональных чисел: корень из 2, корень из 3, логарифм из 4 по основанию 5, sin 3.

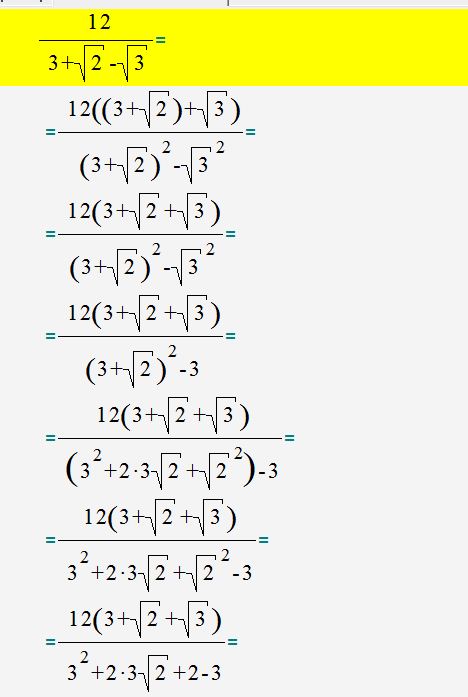
 Если ограничиваться только вещественными числами, то, как известно, действие извлечения корня не всегда выполнимо; корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. В связи с этим уже квадратное уравнение с вещественными коэффициентами не всегда имеет вещественные корни.Это обстоятельство приводит, естественно к расширению понятия о числе, к введению новых чисел более общей природы, частным случаем...
Если ограничиваться только вещественными числами, то, как известно, действие извлечения корня не всегда выполнимо; корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. В связи с этим уже квадратное уравнение с вещественными коэффициентами не всегда имеет вещественные корни.Это обстоятельство приводит, естественно к расширению понятия о числе, к введению новых чисел более общей природы, частным случаем...