числа »

комплексные числа - страница 3

  • Изобразите множество точек комплексной плоскости, удовлетворяющих условию.
    модуль(z-2)>=модуль(z+2*i) (графически)


    Решение: Если z - точка комплексной плоскости, то
    |z-2| - расстояние от точки z до точки 2. (в координатах х, у на плоскости это точка (2,0)).
    |z+2i| - расстояние от точки  z до точки -2i. (в координатах х, у на плоскости это точка (0,2)).
    Значит нас интересует множество точек плоскости, которые находятся дальше от точки (2,0) чем от (0,2). Равноудаленные от них - это точки лежащие на серединном перпендикуляре, который есть прямая с уравнением y=-x. Значит удовлетворяют все точки ниже этой прямой и на ней.

  • Найти действительную и мнимую части комплексных чисел. Указать противоположные и сопряженные. Вычислить модули и изобразить комплексные числа на координатной оси.
    Найти их сумму, разность, произведение, частное и вторую степень первого числа, то есть возвести в квадрат Z1.
    1) Z1=i-2
    2) Z2=1+4i


    Решение: 1) i - 2 = -2 + i (действительная часть = -2, мнимая часть  = i
     противоположное число =  2 - i
    сопряжённое = - 2 - i
     2) 1 + 4i (действительная часть = 1, мнимая часть  = 4 i
     противоположное число = -1 -4 i   
    сопряжённое = 1 - 4i  
     сумма = -1 + 5i
    разность = -2 + i - (1 +4i) = -2 + i - 1 - 4i = -3 -3i
    произведение = ( -2 + i ) * (1 +4i) = -2 + i -8i -4i² = 2 - 7i
    частное = ( -2 + i )/ (1 +4i)   = (-2 +i)(1 - 4i)|(1 + 4i)(1 - 4i) =
    = (-2 +i +8i -4i²)/(1 - 16i³) = (2 + 9i)/17
    (-2 +i)² = 4 - 4i + i² = 3 - 4i
     

  • Найти модуль комплексного числа
    z=4i^9+3i^-18+2i^23+9


    Решение: Следует помнить свойства мнимой единицы: i²=-1. В связи с этим можно записать:
    z=4*i*i^8 +3/i^18 + 2*i*i^22+9=4i*(i^2)^4 +3/(i^2)^9 + 2i*(i^2)^11 + 9=4i(-1)^4 +3/(-1)^9+2i*(-1)^11+9=[-1 в чётной степени = 1, а в нечётной -1]=4i-3-2i+9=2i+6
    Модуль комплексного числа находится по формуле:
    a+ib=√(a²+b²)=√(2²+6²)=√(4+36)=√(4*(1+9))=2√10 - это и будет ответ.

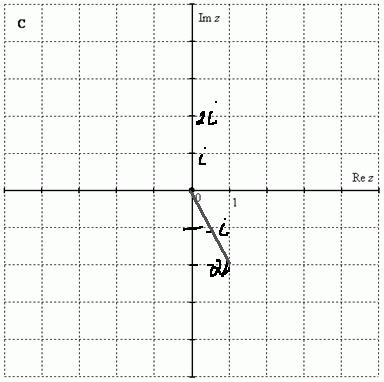
  • Изобразить графически комплексное число и найти модуль и главное значение аргумента: z=1-2i


    Решение: z=1-2i

    1- это вещественная часть числа 

    2i мнимая часть на графике 

    Число обохзначается точкой (1; -2) на координатной плоскости

    Модуль: $$ р=\sqrt{1^2+(-2)^2}=\sqrt{5} $$

    Артумент: $$ cos\alpha = \frac{1}{\sqrt{5}} \\ sin\alpha =- \frac{2}{\sqrt{5}} \\ \alpha=-arcsin\frac{2}{\sqrt{5}} $$

    Ответ: $$ р=\sqrt{5} $$ и $$ \alpha=-arcsin\frac{2}{\sqrt{5}} $$

    z - i - это вещественная часть числа  i мнимая часть на графике  Число обохзначается точкой - на координатной плоскости Модуль р sqrt - sqrt Артумент cos alpha frac sqrt sin...

  • Даны два комплексных числа z1=a+bi и z2=c+di. Найти модуль числа z=2z1z2+z1/z2
    a4 b1 c1 d-1


    Решение: Z=2(a+bi)(c+di)+(a+bi)/(c+di)
    z=2((a*с - b*d)+(ad + bc)i)+((a*с+b*d)/(c^2 + d^2)+(c*b - d*a)/(c^2 + d^2)i)
    z=2((4*1 - 1*(-1))+(4*(-1) + 1*1)i))+((4*1 + 1*(-1))/(1^2 + (-1)^2)+(1*1 - 4*(-1))/(1^2 + (-1)^2)i))
    z=2((4 + 1)+(-4 + 1)i))+((4 -1)/(1 + 1)+(1 + 4)/(1 + 1)i))
    z=2((5-3i))+((3)/(2)+(5)/(2)i))
    z=10-6i + 3/2 + 5/2i
    z=(23/2)+(-7/2)i
    z= 23/2 -7/2i
    z= |23/2 -7/2i|
    z= V((23/2)^2 + (7/2)^2)
    z= V(132.25 + 12.25)
    z= V(132.25 + 12.25)
    z= V(144.5)
    z=12.02

<< < 123 4 > >>