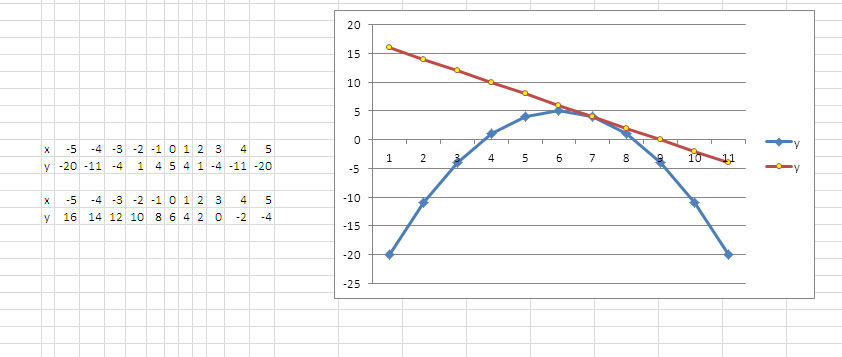
постройте график заданной функции найдите область

с1. сократите дробь: в числителе : х^3-2х^2-9х+18; в знаменателе: (х-2)(х+3)
с2. расстояние между пунктами А и Б = 15 км. лодка вышла из пункта А в 8:00, отправилась в пункт Б, пробыла там 2 часа и вернулась в пункт А в 20:00. определите собственную скорость лодки в км\ч если скорость течения реки = 2 км\ч
с3. известно что графики функций у=-х^2+p и у=-2х+6 имеют ровно одну общую точку. определите координаты этой точки. постройте графики заданных функций в одной системе координат.
с4. в прямоугольном треугольнике абс известны катеты: ас=10, бс=24, найдите радиус окружности, описанной около этого треугольника.
с5. дана равнобедренная трапеция абсд. точка м лежит на основании ад и равноудалена от концов другого основания. докажите, что м - середина основания ад с6. в равнобедренную трапецию абсд с большим основанием аб вписана окружность. из точки с проведена высота сн а из точки н перепендикуляр нф к стороне ад, угол снф = 82 градуса. найдите величину угла снд. п.с.

Решение: с1.

$$ \frac{x^3-2x^2-9x+18}{(x-2)(x+3)}=\frac{x^2(x-2)-9(x-2)}{(x-2)(x+3)}=\\=\frac{(x^2-9)(x-2)}{(x-2)(x+3)}=\frac{(x-3)(x+3)}{(x+3)}=x-3 $$

с2.

т.к. лодка была в пути с 8-00 до 20-00, при этом останавливалась на 2 часа, то в движении она пребывала всего 12-2=10 часов.

Пусть скорость лодки х км/ч. Тогда скорость лодки по течению (х+2)км/ч, а против течения (х-2)км/ч. Тогда из А в Б она ехала 15:(x+2) часа, а из Б в А 15:(х-2) часа.

Получаем, что всего в движении лодка была:

$$ \frac{15}{x+2}+\frac{15}{x-2}=10 $$

Решаем:

$$ \frac{15(x-2)+15(x+2)}{(x+2)(x-2)}=10 $$

$$ \frac{30x}{x^2-4}=10 $$

$$ 30x=10x^2-40 $$

$$ 10x^2-30x-40=0 $$

$$ x^2-3x-4=0 $$

$$ D=b^2-4ac=9+16=25=5^2 $$

$$ x_{1,2}=\frac{-b+-\sqrt{D}}{2a} $$

$$ x_1=4, x_2=-1 $$

второй корень не подходит, т.к. скорость не может быть отриательной.

Ответ: скорость лодки 4км/ч.

с3.

$$ y=-x^2+p; y=-2x+6 $$

графиком первой функции будет парабола. Графиком второй функции будет прямая.

Т.к. в условии сказано, что у них только одна общая точка, то значит что прямая является касательной к параболе (т.к. если это не касательная, то она пересекет обе ветви параболы).

Т.к. прямая является касательной к параболе, то должно выполнятся условие:

$$ \left \{ {{(-x^2+p)’=-2} \atop {-x^2+p=-2x+6}} \right. $$

решаем систему уравнений, из которой находим х (одна из координат точки касания) и р.

$$ \left \{ {{-2x=-2} \atop {x^2-2x+6-p=0}} \right. $$

$$ \left \{ {{x=1} \atop {x^2-2x+6-p=0}} \right. $$

$$ \left \{ {{x=1} \atop {1^2-2*1+6-p=0}} \right. $$

$$ \left \{ {{x=1} \atop {p=5}} \right. $$

получаем уравнение параболы $ y=-x^2+5 $

подставляя значение x в любое из уравнений, находим у:

у=-2*1+6

у=4

Т.о. точка касания имеет координаты (1$4)

График во вложении

с4.

Дано: треуг ABC

уголС=90град

BC=24

AC=10

Найти: R

Решение:

$$ R=\frac{1}{2}*\sqrt{AC^2+BC^2} $$

$$ R=\frac{1}{2}\sqrt{10^2+24^2}=\frac{1}{2}\sqrt{100+576}=\frac{1}{2}*26=13 $$

Ответ:радиус описанной окружности - 13.

с5.

Дано: ABCD - равнобокая трапеция (AB=CD)

M - равноудалена от B и С

Доказать: AM=MD

Док-во:

BM=CM - т.к. М равноудалена от B и С. Отсюда получаем, что треуг MBC - равнобедренный, а значи угол МВС=уголМСВ

т.к. трапеция равноб., то уголВ=уголС

уголВ= уголМВС + угол МВА

уголС= уголМСВ + угол МCD= угол МВС + угол МCD

Получаем, что угол МCD = угол МВА.

Т.о. треугАВМ=треугMCD - по двум сторонам и углу между ними

Отсюда следует, что AM=MD

рисунок во вложении
$с . frac x - x - x x- x frac x x- - x- x- x frac x - x- x- x frac x- x x x- с . т.к. лодка была в пути с - до - при этом останавливалась на часа то в движении она пребыв...$
Функция задана формулой y=6x+19. Определите: а) значение y, если x=0,5 б)значение x, при котором y=1 в) проходит ли график функции через точку А(-2;7)
2 задание
а) постройте график функции y=2x - 4. б) укажите с помощью графика, чему равно значение y при x= 1,5
3 задание
В одной и той же системе координат постройте графики функции: а) y= -2x б) y=3.
4 задание
Найдите координаты точки пересечения графиков функций y=47x -37 и y= -13x + 23.
5 задание (последнее)
Задайте формулой линейную функцию, график которой параллелен прямой y=3x - 7и проходит через начало координат.

Решение: 1.а. Подставляем в формулу значение х, получаем у=22
1.б. Так же подставляем, получаем х=-3
1.в. Проходит
2.а. В таблицу значений х и у подставляем х=0 и х=3, соответственно получаем у=-4 и у=2 и соединяем точки
2.б. Графиком покажете
3. В таблицы заносим данные по х и у и строим графики
4 Графики пересекаются в точке В с координатами (1;10)
5. у=х+1
1) Функция задана формулой y= -x -3. Принадлежит ли графику функции точка A(-1;-4)?
2) Постройте в одной системе координат графики функций y = -2x + 4 и y = 3x - 6. в какой точки они пересекаются?
3) Подберите a, b. c и d так, что графики функций:
а) y = ax - 5 и y = 5x + 6 пересекались;
б) у = 13х + 21 и у = 13х - b были параллельны;
в) y = 7x + 9 и y = cx + d совпадали
4) Постройте график функции y = kx, если известно, что ему принадлежит точка М(-3;18). Найдите:
а) значение Х, при котором у = 6
б) значение у, при котором х = -5

Решение: 1) y=-x-3 A(-1;-4)
-4=1-3⇒-4≠-2 не принадлежит
2) y=-2x+4
x 0 2
y 4 0
y=3x-6
x 0 2
y -6 0
точка пересечения (2;0)
3) а) y = ax - 5 и y = 5x + 6 пересекались⇒a=3
б) у = 13х + 21 и у = 13х - b были параллельны⇒b=5
в) y = 7x + 9 и y = cx + d совпадали ⇒c=7,d=9
4) y=kx M(-3;18)
k=y/x⇒k=18/(-3)=-6
y=-6/x
x -6 -3 -2 -1 1 2 3 6
y 1 2 3 6 -6 -3 -2 -1
a)y=6⇒x=-1
b)x=-5⇒y=1,2
1. Упростите выражения-2x(1-x)+(2x-3)(x+1)=????(3x-1)(3x+1)+(3x+1)во 2 степени=??? 2.решите уравнения 0,5(x+3)=0,4(x-6)+7,7=???? 3.разложите на множители 25а-ab во 2 степени=?????3a во 2 степени-6а+3=????4.решите задачу одно полотно разрезали на 5 равных частей, а другое длина которого на 10 метров больше, на 7 таких же частей. Какова длина каждого полотна????? 5. Постройте график функции y=2x-3. Проходит ли график функции через точку М(-10;25)???

Решение: №1

$$ 2x(1-x)+(2x-3)(x+1)=2x-2x^2+2x^2+2x-3x-3=x-3 $$

$$ (3x-1)(3x+1)+(3x+1)^{2}=9x^2+3x-3x-1+9x^2+6x+1= \\ \ =18x^2+6x=6x(3x+1) $$

№2

$$ 0,5(x+3)=0,4(x-6)+7,7 \\ \ 0,5x+1,5=0,4x-2,4+7,7 \\ \ 0,5x-0,4x=-2,4+7,7-1,5 \\ \ 0,1x=3,8 \\ \ x=38 $$

№3

$$ 25a-ab^{2}=-a(b^2-25)=-a(b-5)(b+5) \\ \ 3a^2-6a+3=3(a^2-2a+1)=3(a-1)^{2} $$

№4

$$ \frac{x}{5}= \frac{x+10}{7} \\ \ 7x= 5(x+10) \\ \ 7x= 5x+50 \\ \ 2x=50 $$

x=25 - длина отрезаемых частей

25*5=125 - длина первого полотна
125+10=135 - длина второго полотна

№5

$$ 2*(-10)-3=25 \\ \ -20-3=25 \\ \ -23 eq 25 $$
ответ: отрезок не проходит через точку М
1. Дана функция у = f(х), где f(x) = 3 - 2х. Вычислите: а) f(0) = б)f(-2) = в)f(3) = г)f(-2a) = д)f(a-1) = x во 2 степени, если -1 < х < или = 3 2. Дана функция у = f(x), где f(x) = 1, если х < или = -1 Вычислите: а) f(-3) = б)f(0) = в)f(2) = 3. Постройте график функции: (функция дана во втором задании)

Решение:
1. f(x) = 3 - 2х. Вычислите: а) f(0) = 3-2·0=3-0=3;б) f(-2) = 3 - 2·(-2)=3+4=7;в) f(3) = 3 - 2·3=3 - 6 = -3;
г) f(-2a) = 3 - 2·(-2а)=3+4а;д)f(a-1) = 3 - 2·(а - 1)= 3 - 2а + 2= 5 - 2а.если 1 < x < 3, то 1 < x² < 9
3 -2·9 < f(x²) < 3 - 2·1;функция у=3-2х убывающая и большему значению аргумента 9 соответствует меньшее значение функции 3-2·9=- 15.
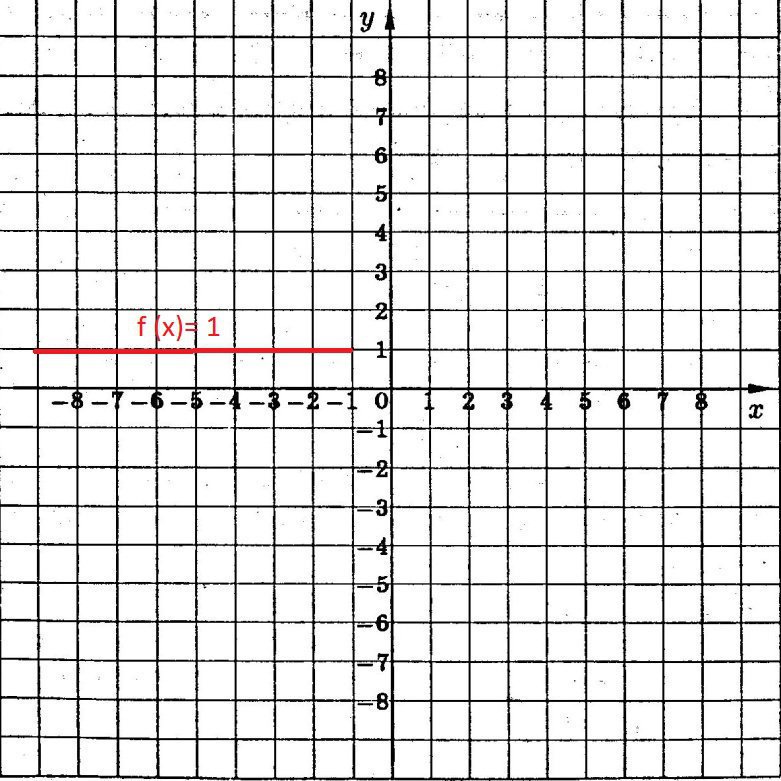
-15 < f(x²) < 1. 2. f(x) =1, если х ≤ -1

а) f(-3) =1
б)f(0) = не определена
в)f(2) = не определена.

3. см. рисунок в приложении.
1) Выполните действия
(64^1/3*8^2/3*49^2/4*81^3/4)^1/2
2) Площадь сечения шара плоскостью 20π м^2, а расстояние от цента шара до секущей плоскости равно 4м. найти объем шара.
3) найдите расстояние от точки М(-4,8,0) до плоскости, заданной уравнением 5х+6у+7х-3=0
4) Путем преобразования постройте график функции y=1/2(x-2)^2*3
5) вычислите площадь ограниченной линиями y=x^3 y=0 x=1 x=2

Решение: 1)
$$ (64^{ \frac{1}{3} }* 8^{ \frac{2}{3} } * 49^{ \frac{2}{4} }*81^{ \frac{3}{4} })^{ \frac{1}{2}}= \ \sqrt{2^{4}*7*3^{3}}= $$3·4·$$ \sqrt{3*7} $$=12$$ \sqrt{21} $$
2)S=20$$ \pi $$ м²
h=4 м
V -
Решение:
S=πr²
r=$$ \sqrt{ \frac{S}{ \pi } }=[tex] \sqrt{ \frac{20 \pi }{ \pi } } = \sqrt{20} $$
По т. Пифагора
R² = r²+h²
R=$$ \sqrt{ (\sqrt{20}) ^{2}+4^{2} }=\sqrt{20+16}= \sqrt{36}=6 \\ V= \frac{4}{3} \pi R^{3} = \frac{4}{3} \pi $$·6³ = $$ 2^{5}*3^{2}* \pi = $$32·9π=288$$ \pi $$
Ответ: 288$$ \pi $$
5)$$ S= \int\limits^a_b {f(x)} \, dx = \int\limits^2_1 {x^{3} } \, dx = \frac{x^{4} }{4} = \frac{ 2^{4} }{4}- \frac{ 1^{4} }{4} = \frac{15}{4} =3.75 $$ ед²
Ответ: 3.75 ед²
№1
Найдите координаты точек пересечения с осями координат графика функции y=-42x+21
№2
На одном чертеже постройте график функции y=2/3 х - 3; у=3,5
у=-0,25х
№3
График прямой пропорциональности проходит через точку С(1;-3)
Задайе эту функцию
№4Не выполняя построений, найдите координат точки пересечения графиков
у=-х/3 и у=12-х
№5 Задайте формулой линейную функцию, графику которой параллелен прямой
у=-х+8 и пересекаются с графиком у=5х+1 в точке, лежащей на оси ординат

Решение: №1. Найдём пересечение с осью х, подставим в функцию вместо х-0:
у=-42*0+21
(0;21)-1ая точка
Теперь ищем пересечение с осью у:
0=-42х+21
-21=-42х
х=-42/21
х=2
(2;0)-2ая точка
№3 В функцию y=kx+b подставим координаты точки С:
у = -3х.
№4Из второй функции подставим значение у в первую функцию:
-x/3=12-x
Домножим обе части на 3, чтобы нам убрать дробь:
-x=36-3x
-x+3x=36
2x=36x=18
Находим точку пересечения, подставив 18 в любую из функций:
-18/3=-6
(18;-6)-координаты точки пересечения двух графиков.
что смогла;)
1) Постройте график линейной функции y=-2x+1
C помощью графика найдите:
a) наименьшее и наибольшее значение функции наотрезке[-1;2]
b) обозначите переменной х, при которых графич. функций расположены на оси Ох
2) Найдите координаты точки пересечения y=3-x,y=2x
3)a) Задайте линейную функцию y=kx, если известно, что ее график параллелен прямой -3x+y-4=0
b) Определите, возрастает или убывает заданная вами линейная функция

Решение: 1) Смотри на картинке у=-2х+1
a) наименьшее и наибольшее значение функции на отрезке[-1;2]
наибольшее - при х=-1 у=-2*(-1)+1=2+1=3
наименьшее - при х=2 у=-2*2+1=-4+1=-3
b) обозначите переменной х, при которых графич. функций расположены на оси Ох
это х=0,5
2) Найдите координаты точки пересечения y=3-x,y=2x
Решим систему уравнений:
$$ \left \{ {{y=3-x} \atop {y=2x}} \right.3-x=2x, 3x=3, x=1, y=2 $$
3)a) Задайте линейную функцию y=kx, если известно, что ее график параллелен прямой -3x+y-4=0
y=3x
b) Определите, возрастает или убывает заданная вами линейная функция
возрастает, т. к. k>0
Функция задана формулой у= - x^{2} -2x -1
Постройте ее график и укажите координаты вершины.
, найти у₀

Решение: Вот график: находим вершину: x верш=2/-2=-1; у верш=-1+2-1=0; т. к а<0, то функция неограниченно убывает, и ее наибольшее значение будет в вершине; а вершина лежит на ох; значит у0=0;
1. Постройте график линейной функции у = -2х+1.
С помощью графика найдите :
а) наименьшее и наибольшее значение функции на отрезке [ - 1; 2 ] ;
б) значения переменной х, при которых у=0.
2. Найдите координаты точки пересечения прямых у = 3- х и у = 2х
3. а) Найдите координаты точек пересечения графика линейного уравнения - 3х + 2у - 6 = 0 с осями координат.
б) Определите, принадлежат ли графику данного уравнения точка К (1/3;3,5)
4. а) Задайте линейную функцию у = кх формулой, если известно, что её график параллелен прямой -3х+у - 4 = 0.
б) Определите возрастает или убывает заданная вами линейная функция.

Решение: 1) а) у max. = 3, y min. = -3.
б) х = 0,5.
2) 3 - х = 2х <=> х = 1
у = 3 - 1 = 2
Координаты точки пересечения - (1; 2).
3) а) С осью Ох:
3х + 2*0 - 6 = 0 <=> х = 2, у = 0.
С осью Оу:
3*0 + 2у - 6 = 0 <=> х = 0, у = 3
б) 3*1/3 + 2*3,5 - 6 = 1 + 7 - 6 = 2 - не принадлежит, т. к. 2 не равно 0.
4) а) -3х + у - 4 = 0 <=> у = 3х + 4.
Так график у = kx параллелен графику у = 3х + 4, то угловые коэффициенты равны => k = 3.
б) у = 3х - возрастающая функция.

1 2 3 > >>

постройте график заданной функции найдите область

Функция задана формулой у= - x^{2} -2x -1 Постройте ее график и укажите координаты вершины. , найти у₀

Функция задана формулой у= - x^{2} -2x -1
Постройте ее график и укажите координаты вершины.
, найти у₀