график функции »

постройте график заданной функции найдите область - страница 2

  • 1) Выполните действия
    (64^1/3*8^2/3*49^2/4*81^3/4)^1/2
    2) Площадь сечения шара плоскостью 20π м^2, а расстояние от цента шара до секущей плоскости равно 4м. найти объем шара.
    3) найдите расстояние от точки М(-4,8,0) до плоскости, заданной уравнением 5х+6у+7х-3=0
    4) Путем преобразования постройте график функции y=1/2(x-2)^2*3
    5) вычислите площадь ограниченной линиями y=x^3 y=0 x=1 x=2


    Решение: 1)
    $$ (64^{ \frac{1}{3} }* 8^{ \frac{2}{3} } * 49^{ \frac{2}{4} }*81^{ \frac{3}{4} })^{ \frac{1}{2}}= \ \sqrt{2^{4}*7*3^{3}}= $$3·4·$$ \sqrt{3*7} $$=12$$ \sqrt{21} $$
    2)S=20$$ \pi $$ м²
    h=4 м
    V -
    Решение:
    S=πr²
    r=$$ \sqrt{ \frac{S}{ \pi } }=[tex] \sqrt{ \frac{20 \pi }{ \pi } } = \sqrt{20} $$
    По т. Пифагора 
    R² = r²+h²
    R=$$ \sqrt{ (\sqrt{20}) ^{2}+4^{2} }=\sqrt{20+16}= \sqrt{36}=6 \\ V= \frac{4}{3} \pi R^{3} = \frac{4}{3} \pi $$·6³ = $$ 2^{5}*3^{2}* \pi = $$32·9π=288$$ \pi $$ 
    Ответ: 288$$ \pi $$
    5)$$ S= \int\limits^a_b {f(x)} \, dx = \int\limits^2_1 {x^{3} } \, dx = \frac{x^{4} }{4} = \frac{ 2^{4} }{4}- \frac{ 1^{4} }{4} = \frac{15}{4} =3.75 $$ ед²
    Ответ: 3.75 ед²

  • №1
    Найдите координаты точек пересечения с осями координат графика функции y=-42x+21
    №2
    На одном чертеже постройте график функции y=2/3 х - 3; у=3,5
    у=-0,25х
    №3
    График прямой пропорциональности проходит через точку С(1;-3)
    Задайе эту функцию
    №4Не выполняя построений, найдите координат точки пересечения графиков
    у=-х/3 и у=12-х
    №5 Задайте формулой линейную функцию, графику которой параллелен прямой
    у=-х+8 и пересекаются с графиком у=5х+1 в точке, лежащей на оси ординат


    Решение: №1. Найдём пересечение с осью х, подставим в функцию вместо х-0:
    у=-42*0+21
    (0;21)-1ая точка
    Теперь ищем пересечение с осью у:
    0=-42х+21
    -21=-42х
    х=-42/21
    х=2
    (2;0)-2ая точка
    №3 В функцию y=kx+b подставим координаты точки С:
    у = -3х.
    №4Из второй функции подставим значение у в первую функцию:
    -x/3=12-x
    Домножим обе части на 3, чтобы нам убрать дробь:
    -x=36-3x
    -x+3x=36
    2x=36x=18
    Находим точку пересечения, подставив 18 в любую из функций:
     -18/3=-6
    (18;-6)-координаты точки пересечения двух графиков.
    что смогла;)

  • 1) Постройте график линейной функции y=-2x+1
    C помощью графика найдите:
    a) наименьшее и наибольшее значение функции наотрезке[-1;2]
    b) обозначите переменной х, при которых графич. функций расположены на оси Ох
    2) Найдите координаты точки пересечения y=3-x,y=2x
    3)a) Задайте линейную функцию y=kx, если известно, что ее график параллелен прямой -3x+y-4=0
    b) Определите, возрастает или убывает заданная вами линейная функция


    Решение: 1) Смотри на картинке у=-2х+1
    a) наименьшее и наибольшее значение функции на отрезке[-1;2]
    наибольшее - при х=-1 у=-2*(-1)+1=2+1=3
    наименьшее - при х=2 у=-2*2+1=-4+1=-3
    b) обозначите переменной х, при которых графич. функций расположены на оси Ох
    это х=0,5
    2) Найдите координаты точки пересечения y=3-x,y=2x
    Решим систему уравнений:
    $$ \left \{ {{y=3-x} \atop {y=2x}} \right.3-x=2x, 3x=3, x=1, y=2 $$
    3)a) Задайте линейную функцию y=kx, если известно, что ее график параллелен прямой -3x+y-4=0
    y=3x
    b) Определите, возрастает или убывает заданная вами линейная функция
    возрастает, т. к. k>0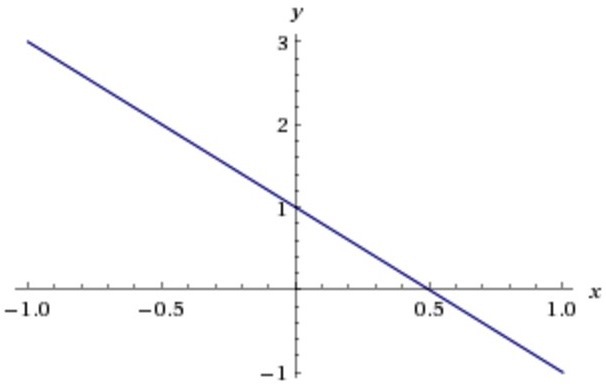

    Смотри на картинке у - х a наименьшее и наибольшее значение функции на отрезке - наибольшее - при х - у - - наименьшее - при х у - - - b обозначите переменной х при которых г...

  • Функция задана формулой у= - x^{2} -2x -1
    Постройте ее график и укажите координаты вершины.
    , найти у₀


    Решение: Вот график: находим вершину: x верш=2/-2=-1; у верш=-1+2-1=0; т. к а<0, то функция неограниченно убывает, и ее наибольшее значение будет в вершине; а вершина лежит на ох; значит у0=0;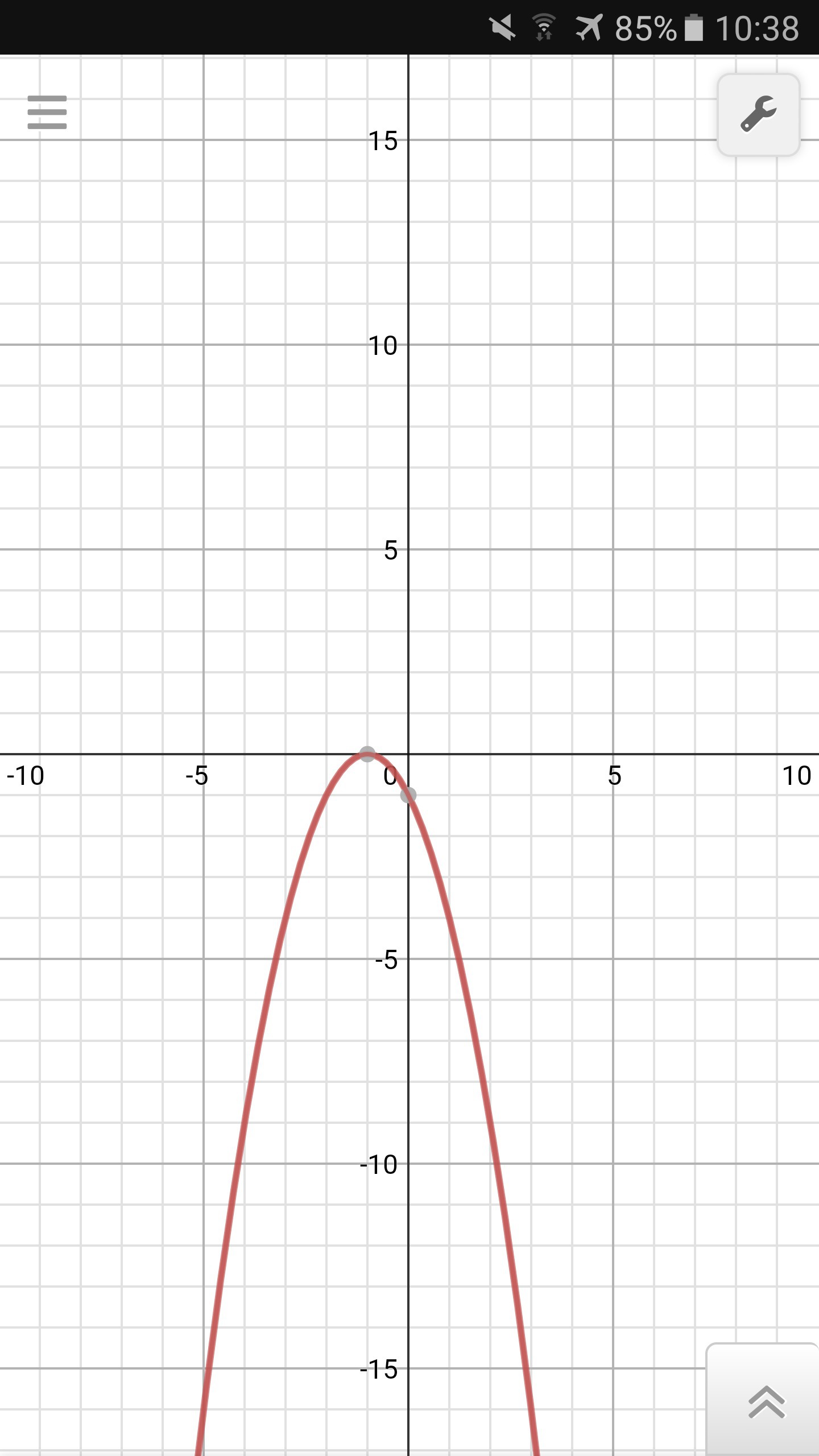

    Вот график находим вершину x верш - - у верш - - т. к а lt то функция неограниченно убывает и ее наибольшее значение будет в вершине а вершина лежит на ох значит у...

  • 1. Постройте график линейной функции у = -2х+1.
    С помощью графика найдите :
    а) наименьшее и наибольшее значение функции на отрезке [ - 1; 2 ] ;
    б) значения переменной х, при которых у=0.
    2. Найдите координаты точки пересечения прямых у = 3- х и у = 2х
    3. а) Найдите координаты точек пересечения графика линейного уравнения - 3х + 2у - 6 = 0 с осями координат.
    б) Определите, принадлежат ли графику данного уравнения точка К (1/3;3,5)
    4. а) Задайте линейную функцию у = кх формулой, если известно, что её график параллелен прямой -3х+у - 4 = 0.
    б) Определите возрастает или убывает заданная вами линейная функция.


    Решение: 1) а) у max. = 3, y min. = -3.
    б) х = 0,5.
    2) 3 - х = 2х <=> х = 1
    у = 3 - 1 = 2
    Координаты точки пересечения - (1; 2).
    3) а) С осью Ох:
    3х + 2*0 - 6 = 0 <=> х = 2, у = 0.
    С осью Оу:
    3*0 + 2у - 6 = 0 <=> х = 0, у = 3
    б) 3*1/3 + 2*3,5 - 6 = 1 + 7 - 6 = 2 - не принадлежит, т. к. 2 не равно 0.
    4) а) -3х + у - 4 = 0 <=> у = 3х + 4.
    Так график у = kx параллелен графику у = 3х + 4, то угловые коэффициенты равны => k = 3.
    б) у = 3х - возрастающая функция.

<< < 12 3 4 > >>