постройте график заданной функции найдите область - страница 4
№1.
Запишите функцию y=kx формулой, чтобы ее график был параллелен графику функции: y=-3x+9. Постройте в одной координатной плоскости их графики и проверьте их параллельность. ( с картинкой.)
№2.
Найдите координаты точки (B) пересечения графиков функций, постройте их графики.
y=-2x-10 И y=-x-7.
№3.
В формуле линейной функции вместо звездочки поставьте такое число, чтобы графики заданных функций были параллельными.
y=4x-5 И y=*x-7.
№4.
График функции y=5x+L проходит через точку E. Найдите значение L, если E(3;6).
№5.
Дана точка A(2;5) и A(3;-6).
1) Постройте график прямой пропорциональности y-kx, проходящую через точку А.
2) По графику найдите значение k для каждой формулы.
3) Для каждой прямой запишите формулу прямой пропорциональности.
Решение: 1. y=-3x+9. функция приподнята на 9. у = -3х - параллельна ей, проходит через начало координат.2.
3.
y=4x-5 И y=4x-7. как и в первом задании, графики параллельны, просто приподняты на разную высоту.
4.
y=5x+L ; E(3;6). подставляем значения х и у в уравнение.
6 = 3*5 + L
6 = 15 + L
L = 6 - 15 = -9
5.
A (2; 5) => 5 = k*2 => k = 2,5 = > y = 2,5x
A(3:6) => 6 = k*3 => k = 2 => y = 2x
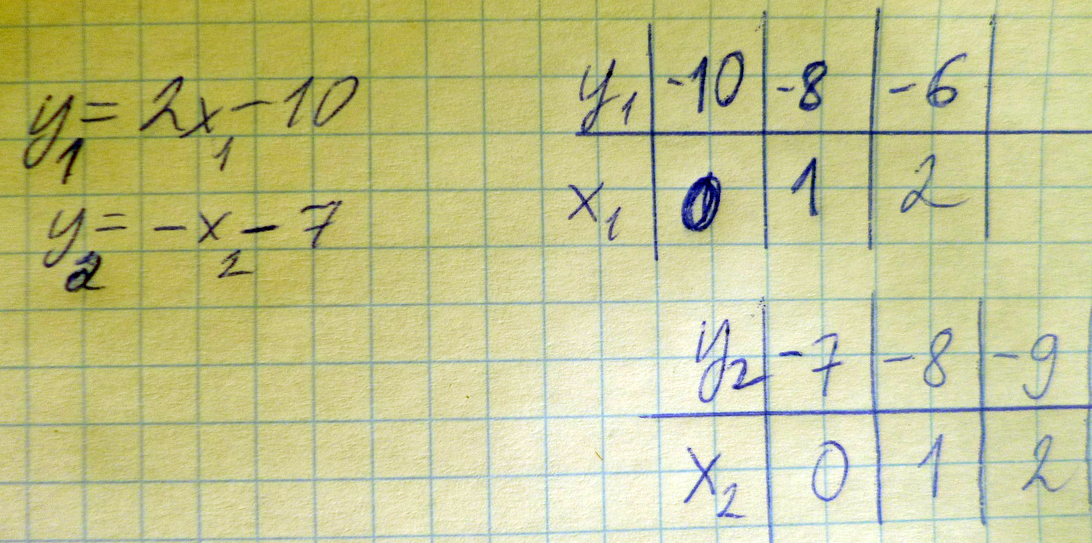
с1. сократите дробь: в числителе : х^3-2х^2-9х+18; в знаменателе: (х-2)(х+3) с3. известно что графики функций у=-х^2+p и у=-2х+6 имеют ровно одну общую точку. определите координаты этой точки. постройте графики заданных функций в одной системе координат. с4. в прямоугольном треугольнике абс известны катеты: ас=10, бс=24, найдите радиус окружности, описанной около этого треугольника. с5. дана равнобедренная трапеция абсд. точка м лежит на основании ад и равноудалена от концов другого основания. докажите, что м - середина основания ад с6. в равнобедренную трапецию абсд с большим основанием аб вписана окружность. из точки с проведена высота сн а из точки н перпендикуляр нф к стороне ад, угол снф = 82 градуса. Найдите величину угла снд.
Решение: с1.$$ \frac{x^3-2x^2-9x+18}{(x-2)(x+3)}=\frac{x^2(x-2)-9(x-2)}{(x-2)(x+3)}=\frac{(x^2-9)(x-2)}{(x-2)(x+3)}=\frac{(x-3)(x+3)}{(x+3)}=x-3 $$
с3.
$$ y=-x^2+p; y=-2x+6 $$
графиком первой функции будет парабола. Графиком второй функции будет прямая.
Т. к. в условии сказано, что у них только одна общая точка, то значит что прямая является касательной к параболе (т. к. если это не касательная, то она пересекет обе ветви параболы).
Т. к. прямая является касательной к параболе, то должно выполнятся условие:
$$ \left \{ {{(-x^2+p)’=-2} \atop {-x^2+p=-2x+6}} \right. $$
решаем систему уравниений, из которой находим х (одна из координат точки касания) и р.
$$ \left \{ {{-2x=-2} \atop {x^2-2x+6-p=0}} \right. $$
$$ \left \{ {{x=1} \atop {x^2-2x+6-p=0}} \right. $$
$$ \left \{ {{x=1} \atop {1^2-2*1+6-p=0}} \right. $$
$$ \left \{ {{x=1} \atop {p=5}} \right. $$
получаем уравнение параболы $$ y=-x^2+5 $$
подставляя значение x в любое из уравнений, находим у:
у=-2*1+6
у=4
Т. о. точка касания имеет координаты (1$4)
График
с4.
Дано: треуг ABC
уголС=90град
BC=24
AC=10
Найти: R
Решение:
$$ R=\frac{1}{2}*\sqrt{AC^2+BC^2} $$
$$ R=\frac{1}{2}\sqrt{10^2+24^2}=\frac{1}{2}\sqrt{100+576}=\frac{1}{2}*26=13 $$
Ответ: радиус описанной окружности - 13.
с5.
Дано: ABCD - равнобокая трапеция (AB=CD)
M - равноудалена от B и С
Доказать: AM=MD
Док-во:
BM=CM - т. к. М равноудалена от B и С. Отсюда получаем, что треуг MBC - равнобедренный, а значи угол МВС=уголМСВ
т. к. трапеция равноб. то уголВ=уголС
уголВ= уголМВС + угол МВА
уголС= уголМСВ + угол МCD= угол МВС + угол МCD
Получаем, что угол МCD = угол МВА.
Т. о. треугАВМ=треугMCD - по двум сторонам и углу между ними
Отсюда следует, что AM=MD
рисунок
2.Для функции f(x)=2(x-1):
а) Найдите общий вид первообразных;
б) Напишите первообразную, график которой проходит через точку А(2;4);
в) Постройте график этой функции.
4. Скорость прямолинейного движущейся точки задано формулой V(x)=t^2-3t+2
Найдите формулы зависимости её ускорения а и координаты х от времени t, если в начальный момент время (t=0) координатах х=-5
Решение: 2. Для функции f(x)=2(x-1):
а) общий вид первообразных F(x) = x^2-2x+C;
б) первообразн fz, график которой проходит через точку А(2;4);F(x) = x^2-2x+4;
в) Постройте график этой функции. )))
4. Скорость прямолинейного движущейся точки задано формулой V(x)=t^2-3t+2
Найдите формулы зависимости её ускорения а и координаты х от времени t, если в начальный момент время (t=0) координатах х=-5
a(t) =2t-3
x(t)=t^3/3-3t^2/2+2t-5Известно, что графики функций y = x^ 2 + p и y = 2x − 2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Решение: Графический способ:
Подберём такое значение p, при котором пересечение будет одно.
Такое p = - 1
y = x^2 - 1
======================решить задачку 1. Постройте графики функций y= -2x + 1 и y= - 1/2x - 1/2 и найдите координаты точки пересечения этих прямых.
Решение: Строите таблицу для каждого уравнения: берете любое Х и считаете для него У, подставляя в уравнение, дальше на фото

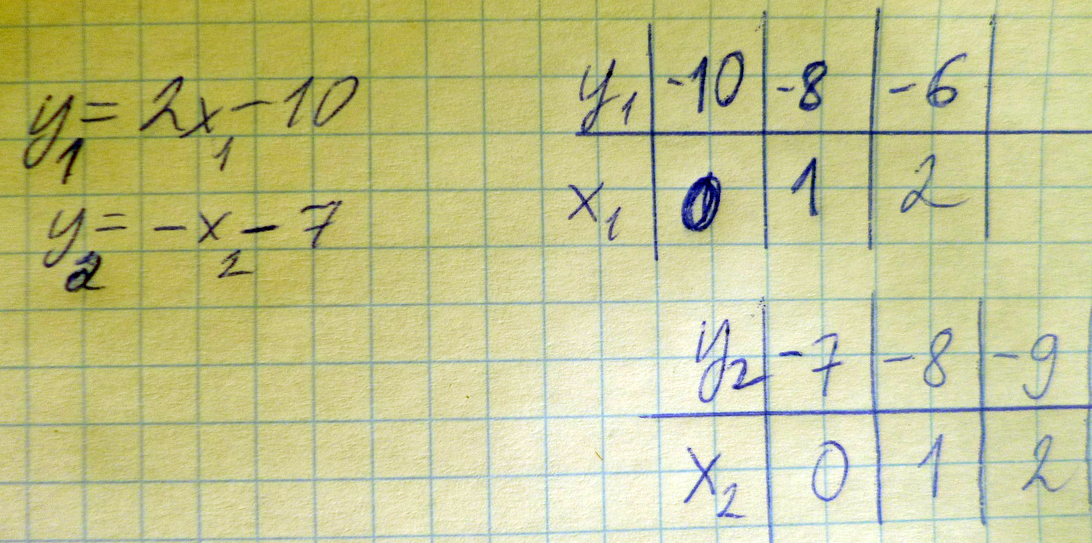
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...