график функции »

построить график функции

  • y=0,25x^2-2x+1 можно ли построить функцию, если дискриминант с корнем?


    Решение: $$ y=0,25x^{2} - 2x + 1 $$

    1. Ветви параболы, являющейся графиком данной функции, направлены вверх, т. к. а=0,25>0

    2. Найдем координаты вершины параболы:

    $$ х=\frac{-b}{2a}=\frac{2}{0,5}=4 $$ 

    y=0,25*16-8+1=-3

    Значит вершина параболы (4; -3)

    3. Точки пересечения с осью ох:

    $$ 0,25x^{2} -2x+1=0 $$

    $$ x^{2} -8x+4=0 $$

    D=64-16=48

    $$ x1=4-2\sqrt{3}, x2=4+2\sqrt{3} $$

    4. Точки пересечения с осью оу:

    у=1

    Далее построить параболу по вершине и найденным точкам (там, где получилось с корнями, взять приближенные значения) 

  • Построить график функции:
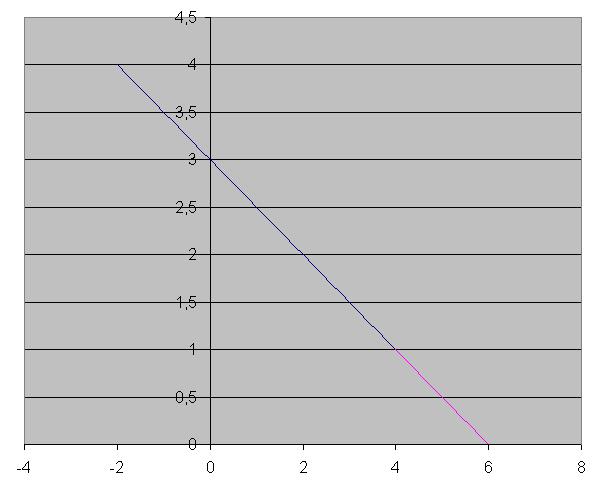
    1)y=1/2x+3
    а) найти координаты точек перечечения этого графика с осями координат.
    б) найти наибольее меньше значение функции на отрезке (-2;4)
    а


    Решение: Предлагаю графическое решение
    график прилагается
    ось х пересекает в точке (6;0)
    ось y пересекает в точке (0;3)
    наибольшее значение функции на отрезке (-2;4) равно 4
    наименьшее значение функции на отрезке (-2;4) равно 1
    смотрим график и наслаждаемся

    Предлагаю графическое решениеграфик прилагаетсяось х пересекает в точке ось y пересекает в точке наибольшее значение функции на отрезке - равно наименьшее значение функции на...

  • 1) не выполняя построения графика функции у=-4х(в квадрате)+5х, найти его наибольшее или наименьшее значение. 2) построить график функции: а) -1/2х(в квадрате). б)-1/2х(в квадрате)-4. 3) А(4;6); В(-4;0). Составить уравнение прямой, проходящие через эти точки. 4) А(3;-4); С(0;5); Е(0;1); В(1;0); Д(0;0); (х-1/2) в квадрате+у(в квадрате)=1/4. Найти координаты окружности и радиуса


    Решение: 1) Функция Y = -4x²+5x
    Максимум при х= 0 У=0
    2) Графики функций а) Y= -1/2x² Y=1/2x²-4 на рисунке
    3) Дано: А(4;6) В(-4;0) Уравнение прямой АВ - У= kX+b
    Коэффициент k = (Ay-By)/(Ax-Bx) = 6/8 = 3/4
    Сдвиг b вычисляем по точке А. Аy=k*Ax+b или b = 6-3/4*4 = 3
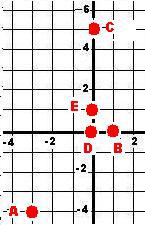
    4) Точки на рисунке. 
    5) Координата центра окружности O(1/2; 0) R=1/2

     Функция Y - x xМаксимум при х У Графики функций а Y - x Y x - на рисунке Дано А В -  Уравнение прямой АВ - У kX bКоэффициент k Ay-By Ax-Bx Сдвиг b вычисляем по точке А. Аy k...

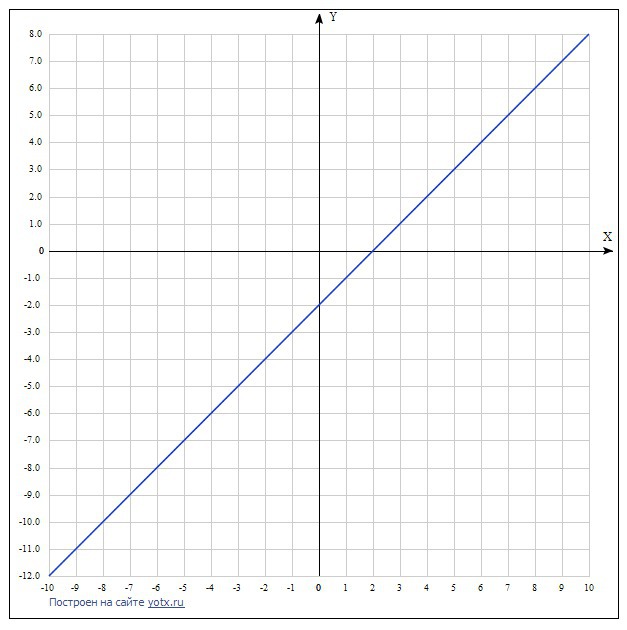
  • Построить график функции у = х - 2. По графику найти:
    а) значение функции, если значение аргумента равно -1; 0; 3;
    б) значение аргумента, если значение функции равно -2; 0; 2;
    в) координаты точек пересечения прямой с осью х и с осью у;


    Решение: Построенный график найдёте .
    $$ a)\ y(-1)=-3,\ y(0)=-2,\ y(3)=1; \\ b)\ y(x_1)=-2,\ x_1=0,\\y(x_2)=0,\ x_2=2,\\y(x_3)=2,\ x_3=4;\\c)\ OX (2;\ 0),\ OY(0;\ -2). $$

    Построенный график найд те . a y - - y - y b y x - x y x x y x x c OX OY - ....

  • Построить график функции y=x^2-4 и найти у>0 при х(?;?)


    Решение: График этой функции - парабола.

    построй по точкам (-3,5),(-2,0),(-1,3),(0,4),(1,3),(2,0),(3,5)

    y>0 при х меньшем или равном -2 и

    х большем или равном 2

    ветви вверх

     область определения вся числовая прямая

     Точки пересечения с осями:

    x=0 y=-4

    y=0 x=+-2

    производная функции y’(x)=2x

    2x=0 x=0 точка локального экстремума

    при переходе через эту точку производная меняет знак с - на +.

    значит x=0-локальный минимум.

    Асимптот нет, ну а точки по которым можно построить уже написали