график функции »

найдите все значения, при которых график функции

  • Постройте график линейной функции y=-2x+6 и сего помощью найдите:1) координаты точки пересечения графика с осью абсцисс.2)все значения аргумента ,прикоторых выполняется неравенство y>0 .3)решение неравенства -2x+6<0 4)значения x ,при которых выполняется неравенство y>6 .


    Решение: без построения
    y=-2x+6 -линейная функция
    абсцисс это ось х
    ордината ось y
    1)
    координаты точки пересечения графика с осью абсцисс
    -2x+6=0
    -2х=-6
    х=3
    те координата (3;0)
    2)
    все значения аргумента ,при которых выполняется неравенство y>0
    т.е
    -2x+6>0
    -2x>-6
    x<3
    3)
    решение неравенства -2x+6<0
    -2x+6<0
    -2x<-6
    при x>3
    4)значения x ,при которых выполняется неравенство y>6 .
    -2x+6>6
    -2х>0
    при x<0



  • Постройте график линейной функции у=х+5 и с его помощью найдите:
    а)координаты точек пересечения графика с осями координат
    б)все значения аргумента, при которых выполняется неравенство у<0
    в)отрезок оси х, на котором выполняется неравенство 0 ≦ у ≦ 5
    г)наименьшее и наибольшее значение линейной функции на отрезке [-4;1]


    Решение: График построй так - при х=0 у=5, при х=-5 у=0. Поставь на плоскости координат точку (0;5) и (-5;0), приложи линейку и проведи прямую через эти 2 точки. Линия графика идет слева вверх направо.
    Пересечения с осями координат уже есть - мы через эти точки и провели прямую.
    у<0 при х∈(-∞, -5)
      0≤у≤5 выполняется при х∈[-5;0]
    на отрезке [-4;1] в силу возрастания функции, наименьшее значение при х=-4 оно равно -4+5=1. Наибольшее значение при х=1 оно равно 1+5=6

  • Наидите наибольшее и наименьшее значение функции на отрезке :f(x)=x³+ 6x²-5 на [0;4]


    Решение: F ’(x)=3x^2 + 12x = 3x( x + 4 )
    f ’(x)=0 при х1=-4, x2=0.
    Начертить ось x, нанести на нее точки, при которых производная равна нулю и границы данного отрезка, x1 и x2 и 4.
    Видим, что от [0;4] функция возрастает (т.к. на этом отрезке производная больше нуля).
    Следовательно, наименьшее значение будет при x=0, а наибольшее - при x=4.
    f(0)=-5, f(4)=64+96-5=155

  • Постройте график функции: y=x^2 Найдите все значения k,при которых точка А(k;1)принадлежит данному графику.


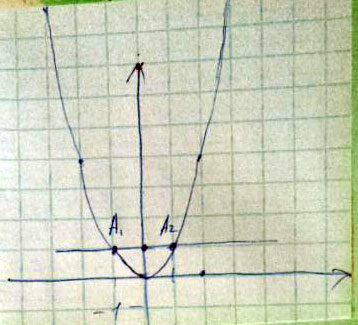
    Решение: y=x^2 - это парабола

    сделав построение, получается:

    ответ: A(-1;1),    A(1;1)

    Парабола y = x², ветви параболы направлены вверх, вершина находится в начале координат.

    Подставим координаты точки А в формулу параболы

    1 = х²

    х = √1

    х = ±1

    При значениях k=1 и k=-1 точка А находится на графике.

    y x - это парабола сделав построение получается ответ A -     A Парабола y x ветви параболы направлены вверх вершина находится в начале координат. Подставим координаты точ...

  • Найдите все целые значения m, при которых график функции y=4x во второй степени + mx+1 расположен выше оси x.


    Решение:

    Функция квадратичная, значит график - парабола. Коэффициент при $$ x^2 $$ больше нуля, значит ветви направлены вверх. Для того, чтобы график данной функции был расположен выше оси OX, нужно, чтобы точка вершины параболы была выше оси OX. Для этого необходимо, чтобы ордината точки вершины была положительной.
    Координаты вершины параболы:
    $$ x_0=\frac{-b}{2a}=-\frac m8\\y_0=4 \left(-\frac m8\right)^2+m\left(-\frac m8\right)+1\\ 4\left(-\frac m8\right)^2+m\left(-\frac m8\right)+1>0\\\frac{4m^2}{64}-\frac{m^2}8+1>0\\ -\frac{4m^2}{64}+1>0\\\frac{m^2}{16}<1\\m^2<16\\-4>m>4 $$
    Целые значения, принадлежащие данному интервалу - это -3, -2, -1, 0, 1, 2 и 3.

1 2 3 > >>