найдите все значения, при которых график функции - страница 2
Найти 15^cos(x) = 3^cos(x) * (0,2)^-sin(x); промежуток [-3п ; -3п\2] ^ это степень перед синусом знак минус
Решение:15^cos(x) = 3^cos(x) * (0,2)^(-sin(x)) ---(0.2 = 1/5 = 5^(-1))
15^cos(x) / 3^cos(x) = 5^sin(x)
(15/3)^cos(x) = 5^sin(x)
5^cos(x) = 5^sin(x)
cos(x) = sin(x)
синус равен косинусу, если х = pi/4 для х из [0; pi/2] и х = 5pi/4 для х из [pi; 3pi/2]
Ответ: -7pi/4, -11pi/4
1) выполните действия:(2a^2*b)^3_____(^-степень)
2) упрастите выражение:(c+d)(d-c) и найдите его значение при с=2,d=0,5
3) вычислите 2^5*3^5
-
6^4
4) решите уравнение:2x-1 =5
-
3
5) из точек А(2,3), B(3,4),C(-1,6) выберите те, которые принадлежат графику функции y=x^2-5
6) выполните разложение на множители : 16a^3-a^7
7) решите уравнение:(x-3)^3+5=x^2-4
8) найдите координаты точки пересечения графиком функций y=3;y=2x-7
9) решите уравнение:x^2=2x-1
10) решите систему уравнений:
2(4x-1)+3y=12
8x-3(2y-5)=11
Решение: 1) (2a^2b)^3 =8a^6*b^32) (2+0.5)(0.5-2)= 2.5*-1.5= -3.75
3) 2^5*3^5/6^4=6^5/6^4=6
4)2x-1=15
2x=16
x=8
5) подставим
3=4-5 нет
4=9-5 да!
Ответ В
6) 16a^3-a^7=a^3(16-a^4)=a^3( 2-a)(2+a)(a^2+4)
7) (x-3)^3+5=x^2-4
x^3-9x^2+ 27x-27+5-x^2+4=0
x^3-10x^2+27x-18=0
(x-6)(x-3)(x-1)=0
x=6
x=3
x=1
8) 3=2x-7
2x=10
x=5
9) x^2=2x-1
x^2-2x+1=0
D=4-4*1*1=0
x=2/2=1
10)
{8x-2+3y=12
{8x-6y+15=11
{8x+3y=14
{8x-6y=-4
{14-3y-6y=-4
{-9y=-18
{y=2
{8x+6=14
{8x=8
{x=1
А) вершина параболы y= x^2+4x+c расположена на один единичный отрезок от оси Ох. Найдите с и постройте график функции. В ходе решения найдите координаты вершины параболы. точки ее пересечения с осями координат, обозначьте найденные точки на графике.
б) найдите все значения х, при которых функция из пункта а) примет неотрицательные значения.
Решение: A)y=x²+4x+c=(x+4)²+(c-4)
c-4=1⇒с=5 или c-4=-1⇒с=3
у=(х+2)²+1 или у=(х+2)²-1
1) у=(х+2)²+1
Парабола у=х² с вершиной в точке (-2;1), точка пересечения с осью оу (0;5), х=-2-ось симметрии, положительна на всей области определения (-∞;∞), убывает при х∈(-∞;-2) и возрастает при х∈(-2;∞)
2) у=(х+2)²-1
Парабола у=х² с вершиной в точке (-2;-1), точка пересечения с осью оу (0;3) и с осью ох (-3;0) и (-1;0), х=-2-ось симметрии, положительна на (-∞;-3) и (-1;∞), отрицательна на (-3;-1), убывает при х∈(-∞;-2) и возрастает при х∈(-2;∞)
Не строя графика функции y=2x^2-13x+26 определите:
1) значения у, при котором х=-3
2) значения х, при которых у=26
3) набольш или наименьш значение функции 4) найдите координаты точек пересечения параболы с осями координат
Решение: Y=2x²-13x+26
1) y(-3)=2(-3)²-13(-3)+26=2*9+39+26=18+65=83
2) y=26 x-
2x²-13x+26=26
2x²-13x=0
2x(x-6,5)=0
x=0 или х-6,5=0
х=6,5
Итак, у=26 при х=0 или при х=6,5
3) y`(x)=(2x²-13x+26)`=2*2x-13=4x-13
y`(x)=0 при 4x-13=0
4(x-3,25)=0
- +
_____________3,25______________
min
y(3,25)=2*(3,25)²-13*3,25+26=21,125-42,25+26=4,875 - наименьшее
***Примечание: Этот же пункт можно сделать проще, без применения производной.
Графиком функции y=2x²-13x+26 является парабола, ветви которой направлены вверх, т. к. а=2 >0, поэтому наибольшего значения функции не существует, а наименьшее значение функция принимает в ординате своей вершины.
х(в)= -(-13)/(2*2)=13/4=3,25
у(3,25)=4,875 - наименьшее
4) Находим точки пересечения функции с осью Ох:
2x²-13x+26=0
D=(-13)²-4*2*26=169-208=-39 <0 => точек пересечения с осью Ох не существует
Находим точку пересечения с осью Оу:
x=0 y(0)=2*0²-13*0+26=26
(0;26) - искомая точка
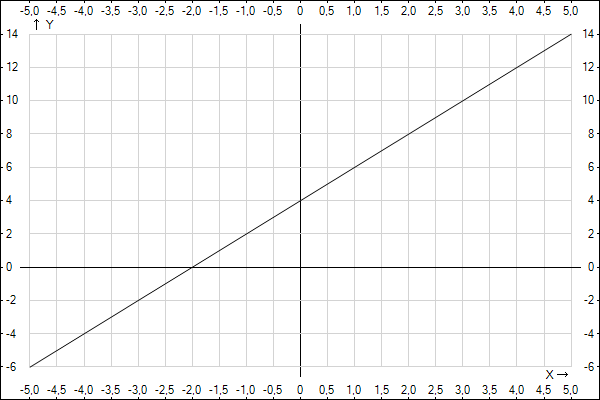
Постройте график линейной функции у=2х+4 и с его помощью найдите: а) координаты точек пересечения графика с осями координат; б) значения аргумента, при которых функция принимает отрицательные значения; в) значения аргумента, при которых функция принимает положительньные значения; г) наибольшее и наименьшее значения функции на отрезке[-3;-1]
Решение: а) пересечение оси Х в точке (-4; 0), пересечение оси У в точке (0; 2)б) х < -4
в) x > -4
г) 1 и 3


 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...