график функции »

найдите все значения, при которых график функции - страница 4

  • Постройте график линейной функции y=2x+4 и с его помощью найдите : a) координаты точки пересечения графика с точкой абсцисс;
    б) значения x, при которых y принимает отрицательное значения;
    в) Yнаим. И Yнаиб. На отрезке [-3;-1].


    Решение: A) Координаты точки пересечения графика с точкой абсцисс: (-2;0);
    б) Значения x, при которых y принимает отрицательное значение: (-∞;-2);
    в) На отрезке [-3;-1]: Y наим. = -2, Y наиб. = 2.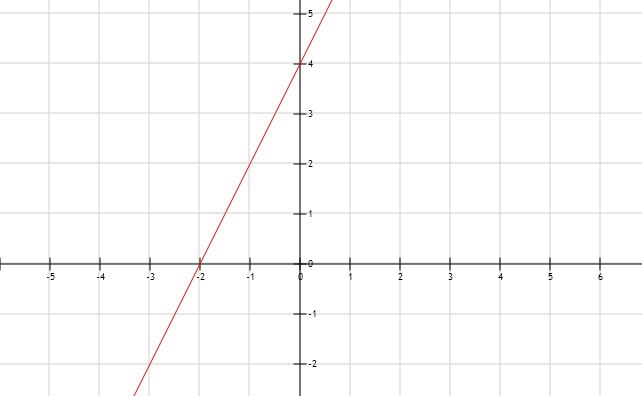

    A Координаты точки пересечения графика с точкой абсцисс - б Значения x при которых y принимает отрицательное значение - - в На отрезке - -  Y наим. - Y наиб. ....

  • Постройте график линейной функции y=-2x+6 с его помощью найдите а) координаты точки пересечения графика с осью абсцисс б) все значения аргумента при которых выполняется неравенство н>0 в) решение неравенств -2x+6<0 г) значения x, при которых выполняется нравенство y>6


    Решение: Строим график по 2-м точкам (0;6) и (1;4).
    а) Точка пересечения с осью ОХ: (3;0). 
    б) Не поняла, что такое "н"  в этой записи  "н>0" ?
    в) Здесь "у" меньше 0, значит этот отрезок прямой, расположен ниже оси ОХ. Т. О. "х" принадлежит промежутку (0; +∞). Скобки круглые, т. к. крайние значения не входят в область определения ф-ции.
    г)  y>6 при х(минус ∞;0)

  • Постройте график линейной функции "y"=-"x"-2 и с его помощью найдите:
    а) координаты точки пересечения графика с осью абсцисс;
    б) значение "x", при которых "y" принимает положительные значения;
    в)"y"(наименьш.) и "y"(наибольш.) и на отрезке [-3;1];


    Решение: Прямая должна пересечь ось абсцисс в -2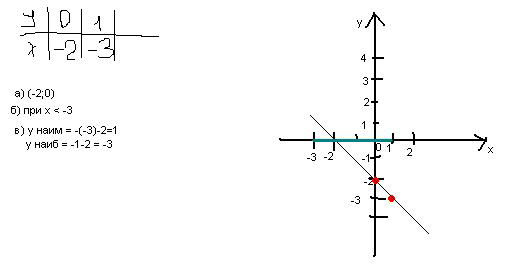Прямая должна пересечь ось абсцисс в -...

  • Найдите координаты точки, через которую проходят графики функций y=2-k-kx при любых значениях параметра k


    Решение: y=2-k-kx

    y=2-k(1+x)

    Графиком функции является прямая, с отрицательным коэффициентом k.

    Смотрим на коффикиенты, 2 - говорит о том, что график подняли на 2 еденицы вверх, (1+x) говорит о том, что график сместили на 1 единицу влево. И того, точка, через которую график функции буде проходить всегда при любых k, имеет координаты: (-1;2)

  • Найдите координаты точки, через которую проходят графики функций y=1-k+kx при любых значениях параметра k. Подстановку вместо k чисел не использовать, т. к. это частный случай.


    Решение: Y = k₁x +(1 -k₁)
    y= k₂x  + (1 -k₂)
    определим точку  пересечения этих прямих
    k₁x +(1 -k₁)= k₂x  + (1 -k₂)
     (k₁ -k₂)x = (k₁ -k₂ )  ;  k₁ ≠ k₂ 
    x=1
    y= k₁*1+(1 -k₁) =1 [  y=k₂*1+(1 -k₂) =1 ]
    ответ:  (1;1)

    Для каждой точки пространства можно провести прямую вида
    y=1-k+kx, проходящую через нее
    выразим к из исходного выражения через значения х и у
    y=1-k+kx
    y-1=k*(x-1)
    k=(y-1)/(x-1)
    выражение неопределено при у=1 и х=1 значит при
    у=1 и х=1 к может принимать бесконечное множество значений
    значит все прямые вида
    y=1-k+kx пересекаются в точке
    у=1 и х=1

<< < 234 5 6 > >>