найдите все значения, при которых график функции - страница 3

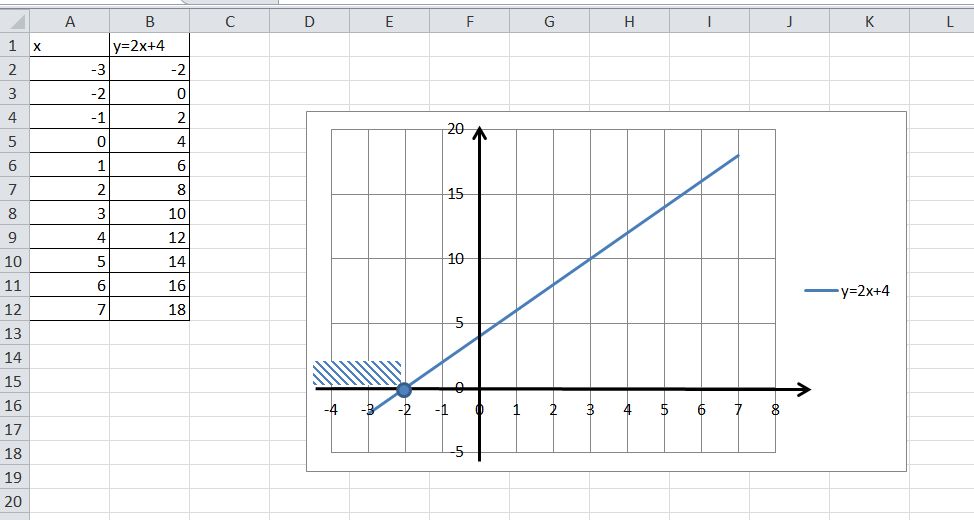
постройте график линейной функции у=2х+4 и с его помощью найдите :
а) координаты точек пересечения графика с осями координат;
б) значение аргумента, при которых функция принимает положительное значение ;
в) значение аргумента, при которых функция принимает отрицательное значение;
г) наибольшее и наименьшее значение функции на отрезке (-3;-1).

Решение: Чтобы начертить график, подставь вместо х любое число (в разумных пределах, а то начертить не сможете.), например, 1. Тогда первая точка будет (1;6). Теперь подставь, например 2. Вторая точка отсюда (2;8).

Теперь построй по этим двум точкам на графике прямую.

А тут уже смотри на график и делай выводы.
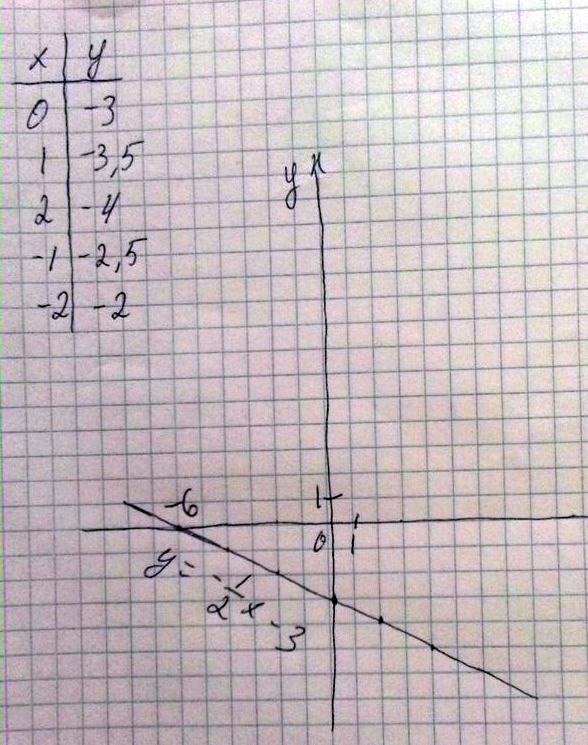
Постройте график линейной функции у=-1/2х-3 с его помощью найдите:
А) координаты точки пересечения графика с осью абсцисс
Б) значения аргумента, при которых функция принимает отрицательные значения
В) наибольшее и наименьшее значения функции на полуинтервале [-2;2)

Решение: а) (-6;0) - точка пересечения с осью абсцисс;
б) от -6 до плюс бесконечности;
в) наибольшее= -2; наименьшего нет, т. к. 2 не входит в полуинтервал [-2;2).
Постройте график линейной функции у=2х+4 и с его помощью найдите а) координаты точки пересечения графика с осью абсцисс б) значения х, при которых у принимает отрицательные значения

Решение: а) точка (-2;0)

б) x∈(-∞;-2) (строго отрицательные)
у=2х+4

Построим таблицу значений. Графиком линейной функции прямая, то достаточно двух значений в таблицу

х -2 0

у 0 4

По таблице в системе координат построить точки, соединить их прямой. Это и есть график функции. Ответ на вопросы можно получить по графику, а можно аналитически

а) 2х+4=0

2х=-4

х=-2

значит точка пересечения графика функции с осью абсцисс имеет координаты (-2; 0)

б)2х+4<0

2x<-4

x<-2

Функция принимает отрицательные значения при хЄ(- ∞; -2)
Постройте график линейной функции у=1/2х+1 и с его помощью найдите: а) координаты точек пересечения графика с осями координат; б) значения аргумента, при которых функция принимает отрицательное значение; в) значения аргумента, при которых функция принимает положительные значения; г) наибольшее и наименьшее значения функции на полуинтервале (-4;2]

Решение: а) (-2;0) - точка пересечения с осью абсцисс, (0;1) - с осью ординат.
б) (-~;-2).
в) (-2;~).
г) наименьшего значения нет, наибольшее значение равно 2.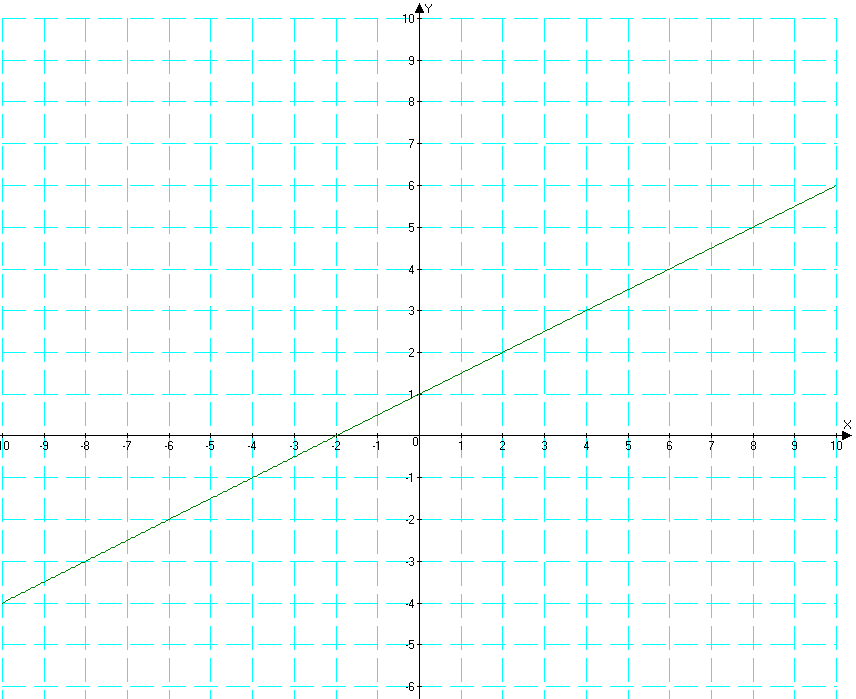
Постройте график линейной функции y=-2x+6 и сего помощью найдите:1) координаты точки пересечения графика с осью абсцисс.2) все значения аргумента, при которых выполняется неравенство y>0.3) решение неравенства -2x+6<0 4) значения x, при которых выполняется неравенство y>6.

Решение: без построения
y=-2x+6 -линейная функция
абсцисс это ось х
ордината ось y
1)
координаты точки пересечения графика с осью абсцисс
-2x+6=0
-2х=-6
х=3
те координата (3;0)
2)
все значения аргумента, при которых выполняется неравенство y>0
т. е
-2x+6>0
-2x>-6
x<3
3)
решение неравенства -2x+6<0
-2x+6<0
-2x<-6
при x>3
4) значения x, при которых выполняется неравенство y>6.
-2x+6>6
-2х>0
при x<0

<< < 1 23 4 5 > >>