найдите координату точек пересечения графика функции - страница 2
Решите систему уравнений; 2y-x=7 x^2-xy-y^2=29 Не выполняя построения, найдите координаты точек пересечения параболы y=x^2+4 и прямой x+y=6
Решение: 2y-x=7x=2y-7
Подставим
4y^2+49-28y-2y^2+7y-y^2=29
y^2-21y=-20
y^2-21y+20=0
D=19^2
y=(21+19)/2=20
y=(21-19)/2=1
x=33
x=-5
Найдем пересечения
x^2+4=6-x
x^2+x-2=0
D=1+8=3^2
x=(-1+3)/2=1 y=5 (1;5)
x=(-1-3)/2=-2 y=8 (-2;8)
2. Периметр прямоугольника равен 28 м, а его площадь равна 40 м^2 (в квадрате). Найдите стороны прямоугольника. 3. Не выполняя построения найдите координаты точек пересечения параболы y=x^2+4 и прямой x+y=6 4. Решите систему уравнений: {2y-x=7 {x^2-xy-y^2=29
Решение: 2. Р=28 м, S=40 м^2составим систему уравнений: xy=40, 2(x+y)=28;
у=14-х, х(14-х)=40, -х^2+14x-40=0
X=4 м
у=14-4=10 м
Ответ: 10 м, 4 м.
3. y=x^2+4, x+y=6.
у=6-х, x^2+x-2=0
Х1=1, Х2=-2
У1=5, У2=8
Ответ: (1;5), (-2;8).
4. {2y-x=7
{x^2-xy-y^2=29
у=(7+х)/2, x^2-28x-165=0
Х1=33, Х2=5
У1=20, У2=6
Ответ: (33;20), (5;6).
1) Найдите стороны прямоугольника, если его периметр 26 см, а площадь - 42^2см
2) Вычислите координаты точек пресечения параболы y=x^2+4 и прямой x+y=6
3) Решите систему уравнений 2y-x=7 x^2 -xy-y^2=29
4) решите систему уравнений 2x+y=7 x^2-y=1
Решение: 2)x+x2+4=6
x2+x-2=0
D=1-4*1*(-2)=9
x1=(-1+3)/2=1
x2=(-1-3)/2=-2
y1=1+4=5
y2=4+4=8
точек пересечения две:
А(1;5)
В(-2;8)
4)
y=7-2x
x^2+2x-7-1=0
x^2+2x-8=0
D=4+32=36
x1=(-2+6)/2=2
x2=(-2-6)/2=-4
y1=7-2*2=3
y2=7-2*(-4)=15
1.
P = 2(a+b) = 26
S = ab = 42
$$ \left \{ {{2(a+b) = 26} \atop {ab = 42}} \right. $$
$$ \left \{ {{a = 13 - b} \atop {(13-b)b = 42}} \right. $$
$$ 13b - b^2 = 42 $$
$$ b2 - 13b + 42 = 0 $$
D = 1
b = 6 или b = 7
a = 7 или a = 6
Ответ: 6 и 7 м.
2.
Решение данной задачи сводится к решению системы из 2х уравнений с 2мя неизвестными:
$$ \left \{ {{y=x^2+4} \atop {x+y=6}} \right. $$
$$ \left \{ {{y=x^2+4} \atop {y = 6-x}} \right. $$
$$ x^2 + 4 = 6 - x $$
$$ x^2 + x - 2 = 0 $$
D = 9
x = -2 или x = 1
y = 6-x
y = 8 или y = 5
Ответ: точки пересечения (-2;8) и (1;5)
3.
$$ \left \{ {{2y-x = 7} \atop {x^2 - xy - y^2 = 29}} \right. $$
$$ \left \{ {{x = 2y-7} \atop {(2y-7)^2 - (2y-7)y - y^2 = 29}} \right. $$
$$ y^2 - 21y +20 = 0 $$
$$ y(y-1) - 20(y-1) = 0 $$
$$ (y-1)(y-20) = 0 $$
y = 1 или y = 20
x = 2y-7
x = -5 или x = 33
Ответ: (-5;1) и (33;20)
4.
$$ \left \{ {{2x+y = 7} \atop {x^2-y=1}} \right. $$
Сложим уравнения
$$ x^2 + 2x = 8 $$
D = 36
x = -4 или x = 2
y = 7-2x
y = 15 или y = 3
Ответ: (-4;15) и (2;3)
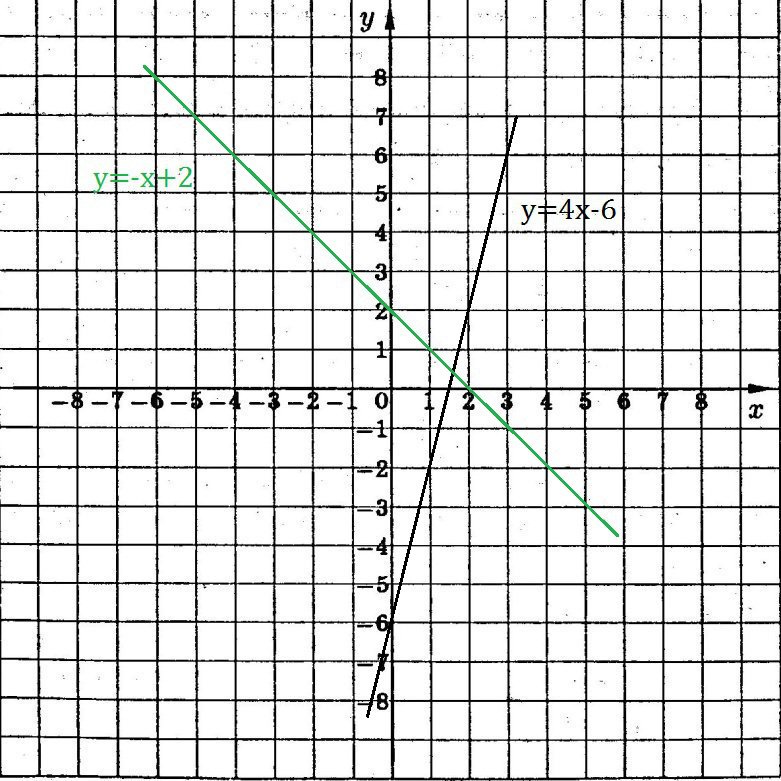
Построить график линейной функции соответствующей системы координат а) y=4x-6
б) y=-x+2
в) y=-3+2
Найдите координаты точек пересечения с осями координат графика линейной функции
а) y=7,5x+45
б) y=2,6x-7,8
Решение:1. См. рисунки в приложении
в) y=-3+2⇒ у=-1 прямая, параллельная оси ох.
Но если в условии опечатка и надо построить прямую у=-3х+2, то график построен там же.
2. Уравнение оси ох: у=0
а)7,5х+4,5=0
7,5х=-4,5
х=-0,6
Точка (-0,6;0).
б)2,6x-7,8=0
2,6х=7,8
х=1/3
Точка (1/3; 0).
1. Найдите координаты точек пересечения параболы y=-x^2+3x-1 и прямой y-x=-9 2.Определите степень многочлена 2√54-3√18/√96-√72
3. Укажите наименьшее из чисел : А. -2^-1 Б. 1^-2 В.2^-2 Г. -1^-1
Решение: $$ \frac{2 \sqrt{54}-3 \sqrt{18}}{ \sqrt{96}- \sqrt{72}} = \frac{\sqrt{9*6*4}- \sqrt{9*2*9}}{ \sqrt{16*6}- \sqrt{9*2*4}}=\frac{6\sqrt{6}- 9\sqrt{2}}{ 4\sqrt{6}- 6\sqrt{2}} $$
a -0,5 $$ (-2)^{-1}= \frac{1}{-2} =-0.5 $$
б 1 $$ 1^{-1}= \frac{1}{1} =1 $$
в 0,25 $$ 2^{-2} = \frac{1}{2^2} = \frac{1}{4} =0.25 $$
г -1 $$ (-1)^{-1}= \frac{1}{-1} =-1 $$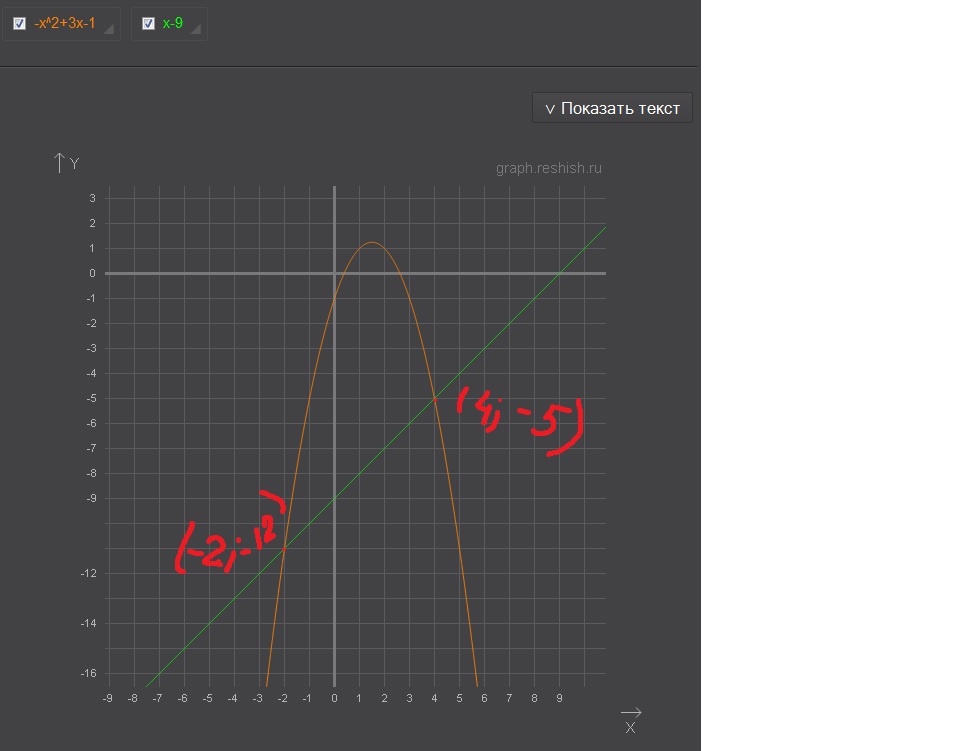



 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...