график функции »

постройте график функции у

  • Постройте график функции у = х^2 - 6х + 5. Определите по графику, на каком числовом промежутке функция принимает отрицательные значения?


    Решение: По графику нужно строить а так 

    y<0

    x^2-6x+5<0

    D=36-4*1*5=4

    x=6+4/2=5

    x=6-4/2=1

    на интервале 

    (1; 5)

    приравниваем функцию к нулю.

    x^2-6x+5=0

    решаем дискриминант и получаем корни х1=5 и х2=1

    можно показать решения либо графическим способом, либо методом интервалов (т.к. это кв. уравнение)

    получается, что ф-я отлицательна (1; 5)

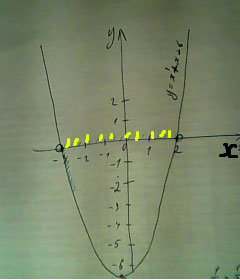
  • На рисунке изображен график функции у=х^2+x-6 (постройте самостоятельно). Используя график, решите неравенство х^2+х-6<0


    Решение: Ответ: х∈(-3;2).  рисунок вложен 

    Решение неравенства на графике заключается в выделении нужного интервала штриховкой (на рисунке - зеленые черточки)  

    Ответ х - .  рисунок вложен  Решение неравенства на графике заключается в выделении нужного интервала штриховкой на рисунке - зеленые черточки   ...

  • Для функции f(x)=sinx найдите одну первообразную и постройте ее график.


    Решение: F(x) = -cosx + C
    Пусть С=0
    F(x) = -cosx - одна из первообразных
    График получается путем зеркального отражения y=cosx относительно оси Ох

    F x -cosx   CПусть С F x -cosx - одна из первообразныхГрафик получается путем зеркального отражения y cosx относительно оси Ох...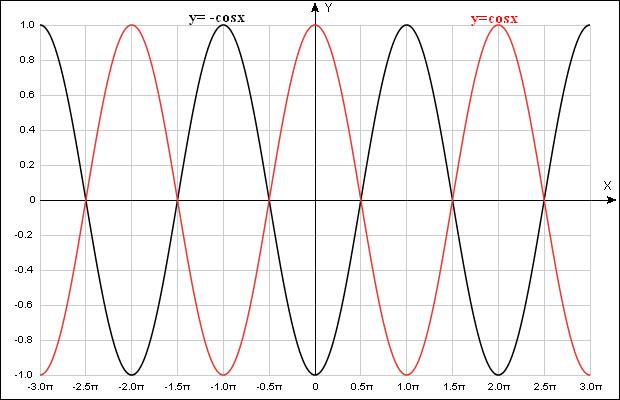

  • Найти обратную функцию и постройте графики обеих функций в одной и той же системе координат: \( y=3 - x^{3} \)


    Решение: У=3-х^3
    Обратная функция:
    3-у=х^3
    корень третьей степени из (3-у)=х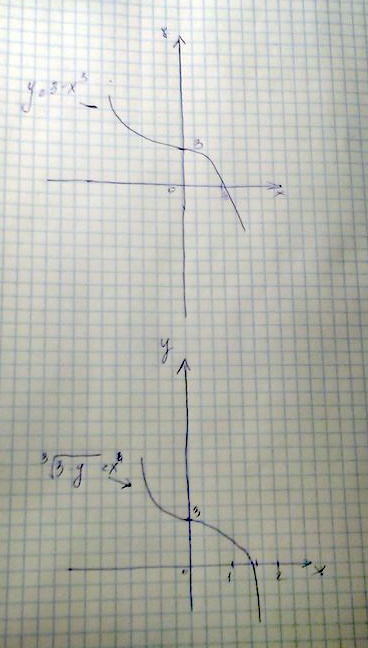
    У -х Обратная функция -у х корень третьей степени из -у х...

  • Постройте график функции у=√х. Найдите: а) наименьшее и наибольшее значения этой функции на отрезке [4;7] б) координаты точки пересечения графика этой функции с прямой х-3у+2=0


    Решение: 1) Построить график функции можно по точкам, берем простые значения:
    у = 0;1;2;3, следовательно х = у2 ; х= 0;1;4;9
    Получается ветвь параболы. Функция - возрастающая, т. к. наибольшему значению аргумента, соответствует большее значение функции. 
    Теперь найдем наибольшее и наименьшее значение функции на отрезке (4;7).
    Функция возрастающая, значит наименьшее значение функции  - в конце интервала с наименьшей абсциссой, т. е. 4; у= √4=2. Наибольшее значение - в конце интервала с наибольшей абсциссой,  т. е.7; у=√7

1 2 3 > >>