постройте график функции у - страница 3

Постройте график функции y=-√x. С помощью графика найдите: а) наибольшее и наименьшее значения функции на отрезке [5;9] б) координаты точки пересечения графика данной функции с прямой x+3y=0

Решение: Решение:
1) Если обычный квадратный корень - функция возрастающая, то со знаком минус, она будет убывать. Значит, наибольшее значение функции: -√5, наименьшее: -√9=-3.
2) Перепишем уравнение в другом варианте:
$$ 3y=-x \\ y=-\frac{x}{3} $$
Строя графики функций, мы обнаружим, что точка пересечения функций: 9,3
Постройте график функции y= корень из х. Найдите
1. наименьшее и наибольшее значения этой функции в отрезке [2;4]
2. координаты точки пересечения графика этой функции с прямой
х-3у+2=0

Решение: 1. Т. к. функция возрастающая, то большему значению аргумента соответствует большее значение функции.
Тогда меньшее значение функции в данном промежутке будет при х = 2,
у = √2.
Наибольшее соответственно при х = 4,
у = √4 = 2.
2. Точек пересечения, как видно на графике, будет 2. Что бы найти их, необходимо решить систему.
{у = √х,
{х - 3у + 2 = 0;
Подставим значение у из первой части системы во вторую.
х - 3√х + 2 = 0,
Вводим замену переменной, √x = t, t ≥ 0.
t² - 3t + 2 = 0,
D = 3² - 4*2 = 1,
t = (3 ± 1)/2,
t1 = 1, t2 = 2.
Вернёмся к х:
√х1 = 1, √х2 = 2
х1 = 1, х2 = 4
Подставим в первое уравнение системы:
у1 = √1 = 1,
у2 = √4 = 2.
Ответ:
1. Наим.: √2; наиб.: 2.
2. (1; 1), (4; 2).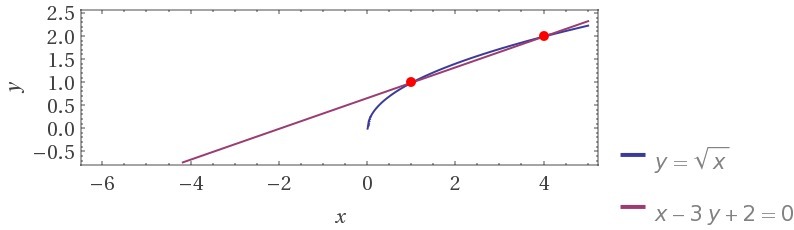
Постройте график функции У=√х.
Найдите:
а) Наименьшее и наибольшее значение этой функции на отрезке [4;7]
б) координаты точки пересечения графика этой функции с прямой х-2у =0

Решение: График функции y=√х веточка параболы. В начале с точкой (0;0). Возрастает на всем промежутке определения.

а) Так как функция возрастает, то наибольшее значение в крайней правой точке, наименьшее - в крайней левой.

y наибольшее = √7

у наименьшее = √4 = 2

б) Решим систему

y=√x

x-2y=0

y=√x

y=0,5x

0,5x=√x

x=2√x

x-2√x=0

√x(√x-2)=0

√x=0

√x=2

x=0

x=4

x=0

y=0

x=2

y=4
На одной координатной плоскости Oxy постройте графики линейных функций y=f(x) и y=g(x) и найдите координаты их точки пересечения.
1)f(x)=2x-1, g(x)=-x+2
2)f(x) =6-3x, g(x)=2x-4
3)f(x)=-x+3, g(x)=1,5x-2
4)f(x)=-0,5+1, g(x)=-5-2x
Пж

Решение: Построить график функции У=2Х-1 можно по 2 точкам:
если Х=0, то У=2*0-1=-1
и У=0 при 2Х-1=0, т. е. Х=1/2.
Соединяем эти точки - получаем прямую, изображающую зависимость f(x)=2x-1
Аналогично - находим точки пересечения с осью Х и осью У прямой У=-Х+2.
При Х=0 У=0+2=2.
и У=0 при 0=-Х+2, Х=2.
Соединяй эти точки - получай вторую прямую, изображающую зависимость g(x)=-x+2.
Пересечение этих прямых - точка, которая одновременно относится к ОБОИМ прямым, удовлетворяет одновременно ДВУМ условиям: f(x)=2x-1 и g(x)=-x+2.
На графике найдете координаты этой точки, а можно решить СИСТЕМУ этих двух УРАВНЕНИЙ:
2х-1=-х+2 при (переносим Х в одну сторону от знака =, цифры - в другую) 3Х=3, т. е. Х=1.
При этом У=2х-1=2*1-1=1 (можно было считать и так: У=-х+2-1+2=1).
ТАК получилось на графике? Координаты точки пересечения этих прямых (1;1)?
Аналогично - все остальные примеры.
Известно, что графики функций y = x^2 - p и y = 2х + 3 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики функций в одной системе координат

Решение: У=х²-р и у=2х+3
найдем точки пересечения:
х²-р-(2х+3)=0
х²-2х-(3+р)=0, решаем через дискриминант
Д=4+4(3+р)
Д=4(4+р), для того, что бы при решении получился один корень, нужно что бы дискриминант =0, тогда
4(4+р)=0
р= -4. Теперь подставим в исходное выражение:
х²-2х-(3-4)=0
х²-2х+1=0
(х-1)²=0, х=1, а у=2·1+3=5
точка пересечения у=х²+4 и у=2х+3 - точка (1;5)
Думаю с построением графиков проблем не возникнет.

<< < 1 23 4 5 > >>

постройте график функции у - страница 3

Известно, что графики функций y = x^2 - p и y = 2х + 3 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики функций в одной системе координат