график функции »

постройте график функции у - страница 2

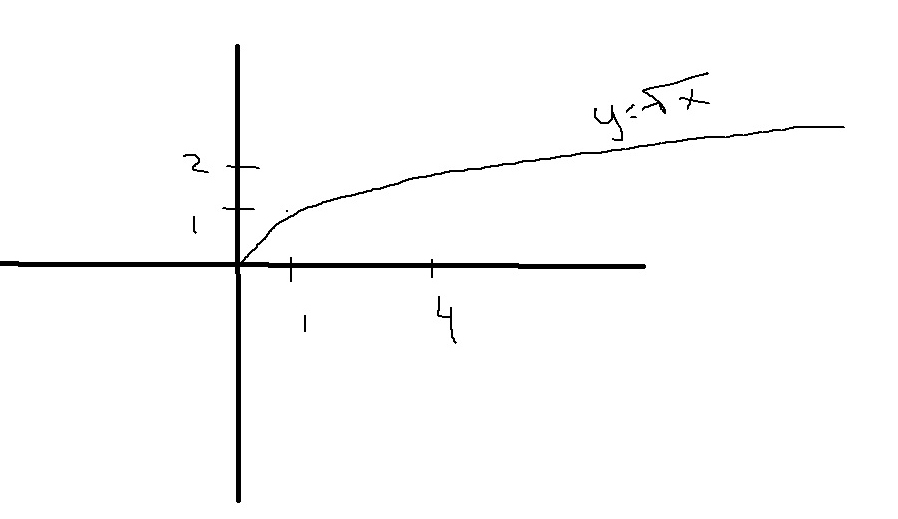
  • Постройте график функции γ=√х. Найдите:
    а) наименьшее и наибольшее значения этой функции на отрезкеx [4;7];
    б) координаты точки персечения графика этой функции с прямой х-2γ=0
    решите з


    Решение: а) наименьшее и наибольшее значение можно посмотреть по графику

    Наименьшее y=2;

    Наибольшее y=sqrt(7) (sqrt(число) - корень квадратный из числа)

    б) Координаты пересечения с прямой х-2γ=0

    Для начала, приведем эту прямую к нормальному виду.

    2y=x

    y=x/2

    Теперь посмортим на его свойства, это прямая, проходящяя через начало координат, точка(0;0) (уже 1 точка) и через точку (4;2) черет эту же точку проходит и наш график y=sqrt(x)

    Значит всего 2 точки пересечения (0;0) и (4;2)

    Почему нету больше точек? Если построить график функции прямой, то мы увидим что она гараздо прогрессивней идет вверх че sqrt(x), значит они бошльше не пересекуться, и точек пересечения не будет.

    а наименьшее и наибольшее значение можно посмотреть по графику Наименьшее y Наибольшее y sqrt sqrt число - корень квадратный из числа б Координаты пересечения с прямой х- Для...

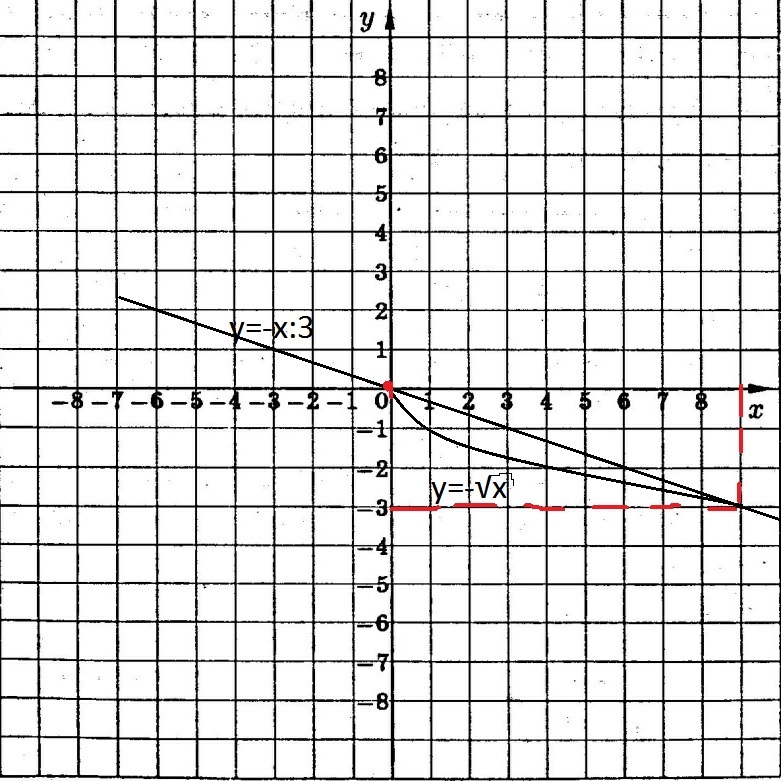
  • Постройте график функции \(y=-\sqrt{x}\). Найдите наименьшее и наибольшее значение этой функции на отрезке[5;9]
    координаты точки пересечения графика этой функции с прямой х+3у=0


    Решение: $$ y=-\sqrt{3}\\y_{max}=-\sqrt{5}\\y_{min}=-\sqrt{9}=-3 \\ x+3y=0\\3y=-x\\y=-\frac{x}{3} $$

    координаты точки пересечения графика этой функции с прямой х+3у=0:

    (0;0) u (9;-3)

    y - sqrt y max - sqrt y min - sqrt - x y y -x y - frac x координаты точки пересечения графика этой функции с прямой х у u -...

  • Постройте график функции y=корень x. Найдите а) наименьшее и наибольшее значение этой функции на отрезке [4;7]. б) координаты точки пересечения графика этой функции с прямой x-2y=0


    Решение: Построить график по точкам х=0 у=0 х=1 у=1 х=4 у=2
    ф-я возрастающая на всей области определения и значит наименьшее значение на отрезке √4=2 наибольшее √7
    x-2y=0 ⇒y=x/2 √x=x/2 ⇒ x-2√x=√x(√x-2)=0
    x=0 y=0 и x=4 y=4/2=2 координаты точек пересечения

  • В одной системе координат постройте графики функций y= -0,5x и y=2. Найдите координаты их точки пересечение


    Решение: Первая прямая  у= -0,5х проходит через начало координат, след
    х= 0      4
    у= 0     -2
    вторая прямая у=2 параллельна оси ОХ и проходит через точки
    х= 0    -2
    у= 2     2
    Строим графики в системе координат по точкам.
    По графику смотрим и видим, что точка пересечения А(-4;2).

  • Постройте график функции y=корень из x
    Найдите: а) наименьшее и наибольшее значения этой функции на отрезке [4;7]
    б) координаты точки пересечения графика этой функции с прямой x-2y=0


    Решение: а) y=sqrt(x) - монотонно возрастающая функция. Наименьшее и наибольшее значения будут достигаться в точках, соответствующих наименьшему и наибольшему значению аргумента промежутка.
    ymin=2

    ymax=sqrt(7) 

    б) Представим x-2y=0 как y=x/2

    Накладываем ОДЗ, составляем уравнение sqrt(x)=x/2, решаем как квадратное.
    x=0 x=4. 

<< < 12 3 4 > >>