график функции »

график функции

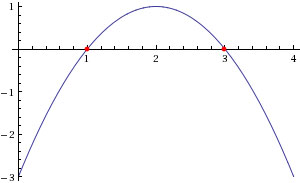
  • Функция: у= - x^2+4x-3. Определите по графику, на каком числовом промежутке функция принимает положительные значения.


    Решение: Функция: у= - x^2+4x-3.

    приравняем к 0

    найдем точки пересечения с ОХ

    x1 = 1 ; x2= 3

    по графику видно , что на промежутке (1 ; 3) функция принимает положительные значения.

    Функция у - x x- . приравняем к найдем точки пересечения с ОХ x x по графику видно что на промежутке  функция принимает положительные значения....

  • A. функция задана формуллой у=-3x+1. принадлежит ли точка М (-1;4) Б. Функция задана формулой y= 2 : xво второй степини -1. Принадлежит ли точка (0;2)графику этой функции? В. При каком b точка K(0;5) принадлежит графику функции y=4x во второй степини х+b.


    Решение:

    А: нет, т.к. график проходит через координаты (2;7), (1;4), (0;1), (-1;-2).

    Б: нет, т.к. x=0, y=2, а т.к. x в знаменателе, то равнятся нулю он не может.

    В: x=0, y=5; 5=4*0 в степени 2*0+b, 0 в степени 2*0+b = 5/4; 0 в степени 0+b = 1,25;  т.к 5-9 классы через логарифмы не рещаете, а оно дальше рещается именно так.. 0 в любой степени будет равнятся 0 и уравнение  будет неверным.

  • Объясните алгоритм построения функции, например такой: у=-х^2+7х-12 что нужно найти для построения конкретно таких графиков?


    Решение: Дана функция с модулем, её необходимо вскрыть.
    Свойство модуля
    |x| = х, если x\(\geq\) 0
    |x| = -x, если x<0

    Какой у нас геометр. смысл у модуля?(Расстояние).
    Вот во втором случае у нас подразумевается ОТРИЦАТЕЛЬНОЕ ПОДМОДУЛЬНОЕ ВЫРАЖЕНИЕ, при его ВЫСВОБОЖДЕНИИ мы обязаны поменять знак на ПРОТИВОПОЛОЖНЫЙ.
    Иначе говоря, исходная функция разбивается на две области определения.
    В первом случае вы просто снимаете модуль;
    Во втором - МЕНЯЕТЕ ЗНАК, в соответствии с "ПОДМОДУЛЬНОЙ ОБЛАСТЬЮ ОПРЕДЕЛЕНИЯ". Что я имею в виду:
    |x-2|
    нуль подмодульного выражения. 2.
    Если х-2<0, т. е. x<2, то при снятии модуля знак меняем -х+2.
    Если больше либо равно, просто снимаем модуль. Эти модули включаются в систему, раскрывать в соответствии с моим правилом.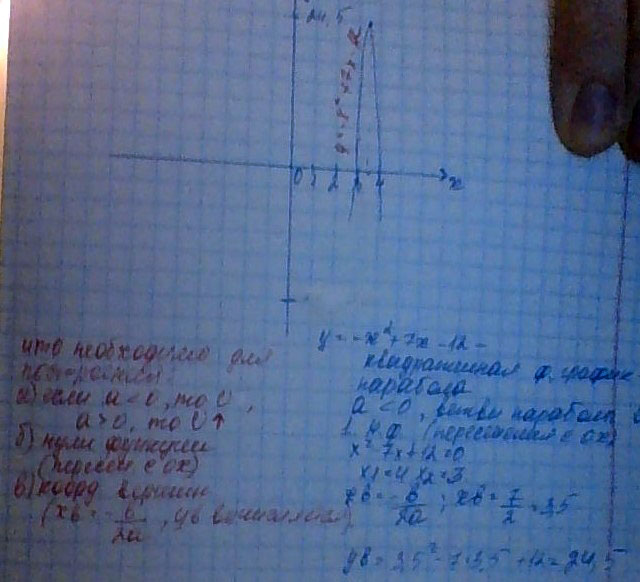

    Дана функция с модулем е необходимо вскрыть.Свойство модуля x х если x geq x -x если x...

  • Построить график дробно-линейных функций (Гиперболы)y= x-2/x+2


    Решение: Y=x-2/x+2=-4/(x+2)+1
    Значит, чтоб построить график надо: 
    1) Построить график функции y=1/x 
    2) Зеркально отразить его относительно оси x
    3) Растянуть от оси x в 4 раз
    4) Выполнить параллельный перенос гиперболы, при котором её центр (0;0) переходит в точку (−2;1)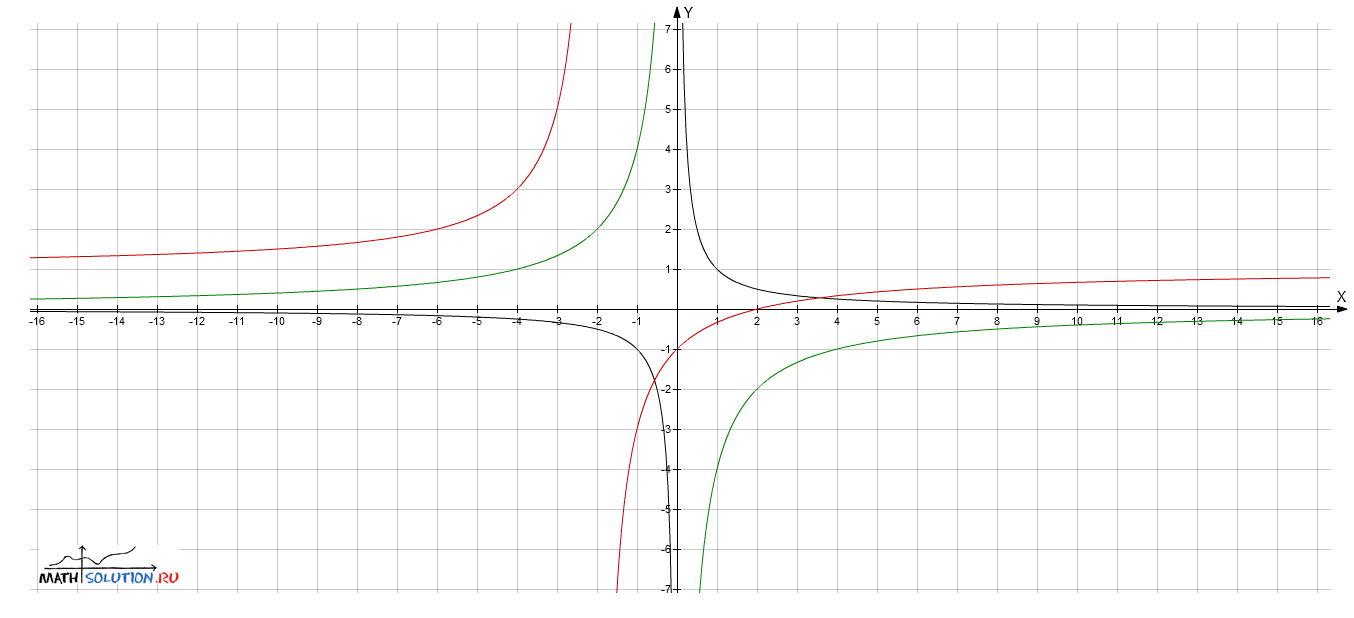Y x- x - x Значит чтоб построить график надо    Построить график функции y x   Зеркально отразить его относительно оси x  Растянуть от оси x в   раз  Выполнить параллельный п...

  • Найти координаты пересечения графиков функций 4х-3у=-1 и 3х+2у=12


    Решение: 4х-3у=-1 |*2

    3х+2у=12|*3

    8x-6y=-2

    9x+6y=36

    -

    17x=34

    x=2

    4*2-3y=-1

    8-3y=-1

    -3y=-9

    y=3

    Если два графика пересекаются то они имеют общую точку, т. е. будут иметь одинаковые координаты оба графика в этой точке.

    В общем надо выразить либо x либо y и приравнять уравнения

    Допустим выражу я x из второго уравнения:

    x=(12-2y)/3

    подставим в первое уравнение x:

    (12-2y)*4/3-3y=-1

    (48 -8y)/3-3y=-1

    домножим обе части уравнения на 3 чтобы избавиться от знаменателя:

    48-8y-9y=-3

    -17y=-51

    (1)y=3

    подставим это значение в любое из первоночально данных уравнение, допустим в первое:

    4x-9=-1

    (2)x=2

    вот собственно и точки пересечения ((1) и (2))

    Ответ: пересекаются в точке A(2;3). 

1 2 3 > >>