график функции »
график функции - страница 3
На графике функции y=-3x+10 найти точку пресечения координата которой равна ее абсциссе
Решение: Нужно решить систему уравнений
у=3х+10
у=х
вычтя из первого уравнения второе, получим 0=2х+10 х= -5 у= -5
координаты искомой точки (-5; -5)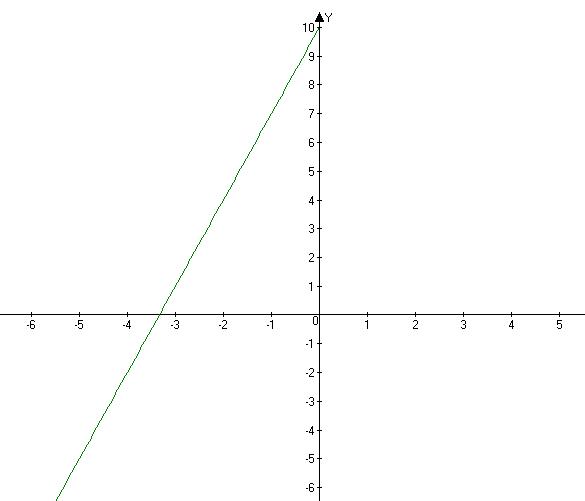
Найти У наиб. и У наим. для линейной функции у=-1.5х+3.5 на луче [0, +Бесконечность)
Решение: Откуда взялась точка (3;-1)?
Ответ: функция у = -1.5х+3.5 - линейная, поэтому достаточно двух точек для ее построения, вторая точка получается при х = 3
у (3) = -1,5*3+3,5 = -1
Так как функция убывающая, то Наибольшее значение функции на интервале $$ [0;+\infty] $$ будет в точке х =0
у (0) = -1,5*0+3,5 = 3,5 - наибольшее значение функции
Наименьшее значение при $$ x \to +\infty $$ стремится к $$ y \to -\infty $$
Найти на графике функции y=4/x точки, ближайшие к началу координат
Решение: Необходимо найти кратчайшее расстояние от центра О(0;0) до точек графика. Составим функцию и найдем ее производную (см. вложенный файл)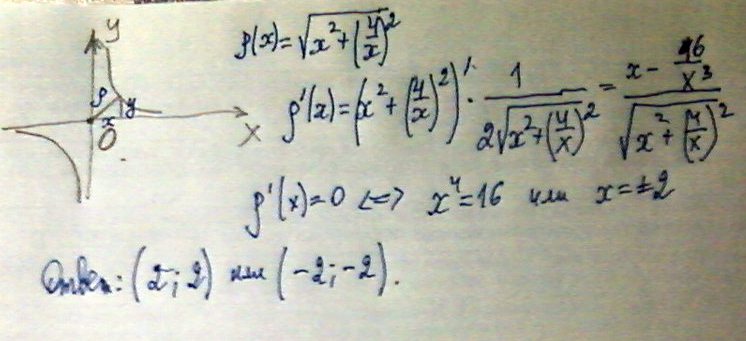
Найдите значения k и b функции вида у = kх + b, если известно, что график функции проходит через точки M (3;9) и N (-6;-9). Найдите координаты точки пересечения этого графика с прямой у=6
Решение: У=кх+b
т. М (3; 9)
т.N (-6;-9)
1) {9=3k+b | умножим на "-1" {-9=-3k-b
{-9=-6k+b {-9=-6k+b
Складываем два уравнения системы:
-9-9=-3к-6к
-18=-9к
к=2
9=3*2+b
9=6+b
b=3
y=2x+3
2) Найдем точки пересечения графиков у=2х+3 и у=6:
6=2х+3
6-3=2х
2х=3
х=1,5
т. А (1,5; 6) - точка пересечения графиков.
Ответ: т. А (1,5; 6)Найдите все точки графика функции у=(х^2+2х-20)/(х-4), имеющие целочисленные координаты. нужно решение
Решение: 1) Разделим столбиком многочлен на многочлен, получим:
$$ y= \frac{x^{2}+2x-20}{x-4}=x+6+\frac{4}{x-4} $$
2) Чтобы у было целым, нужно чтобы дробь $$ \frac{4}{x-4} $$ была сократима.
Это возможно, если знаменатель является делителем 4, т. е. он равен:
2.1) $$ x-4=4 \\ x_{1}=8 $$
2.2) $$ x-4=-4 \\ x_{2}=0 $$
2.3) $$ x-4=2 \\ x_{3}=6 $$
2.4) $$ x-4=-2 \\ x_{4}=2 $$
2.5) $$ x-4=1 \\ x_{5}=5 $$
2.6) $$ x-4=-1 \\ x_{6}=3 $$
3) Найдем ординаты точек:
$$ y(0)=0+6+\frac{4}{0-4}=6-1=5 \\ y(2)=2+6+\frac{4}{2-4}=8-2=6 \\ y(3)=3+6+\frac{4}{3-4}=9-4=5 \\ y(5)=5+6+\frac{4}{5-4}=11+4=15 \\ y(6)=6+6+\frac{4}{6-4}=12+2=14 \\ y(8)=8+6+\frac{4}{8-4}=14+1=15 $$
Ответ: (0;5), (2;6), (3;5), (5;15), (6;14), (8;15)


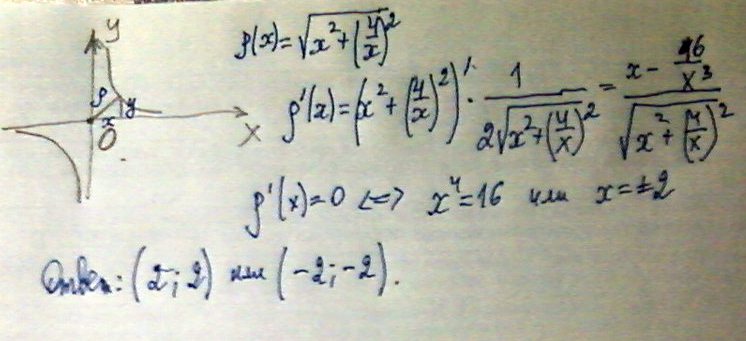
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...