график функции »

область определения функции - страница 21

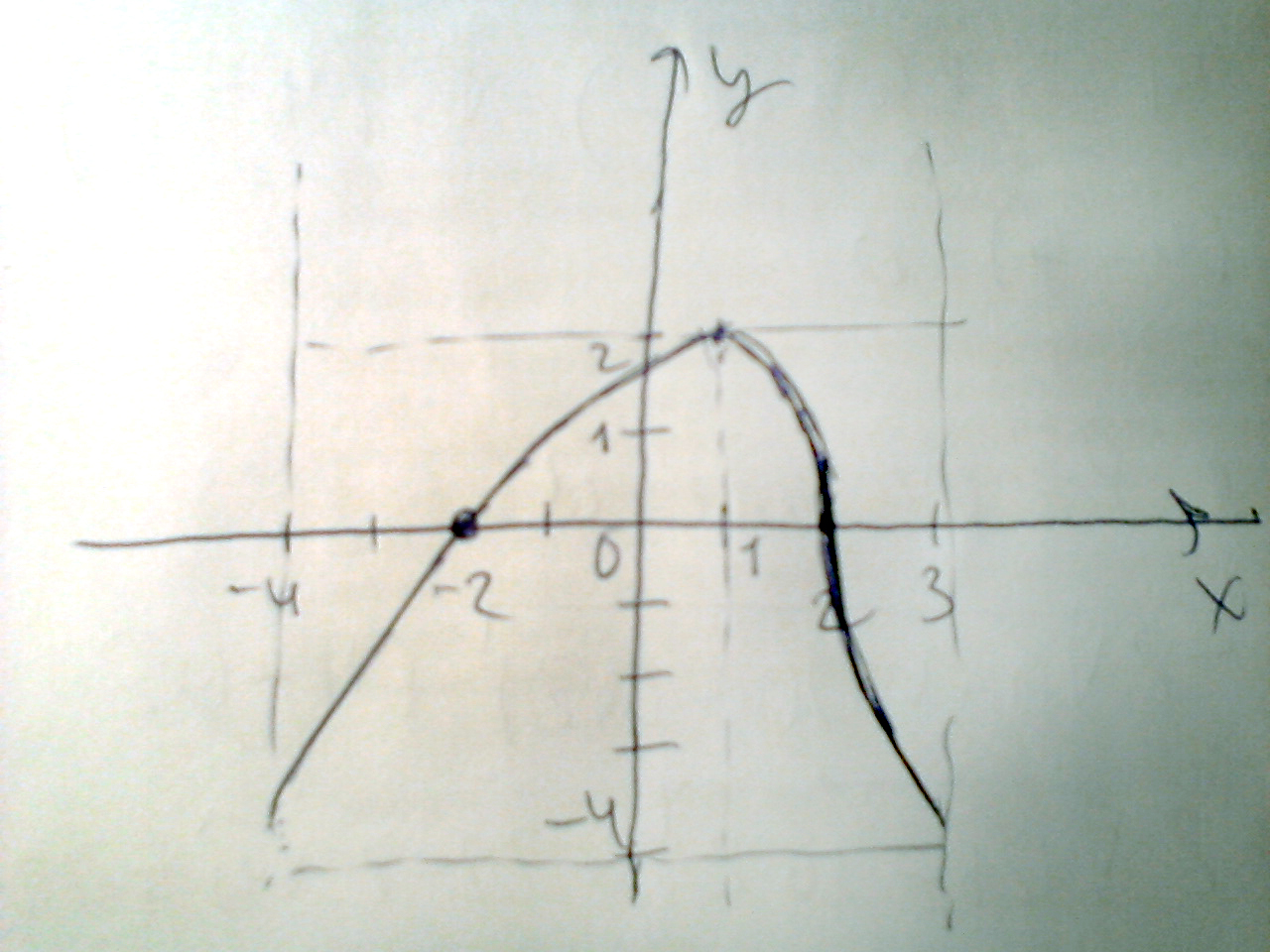
  • Изобразите график функции, зная, что: а) область определения функции есть промежуток [-4;3] б) значения функции составляют промежуток [-4;2] в) производная функции положительна на (-4;1), отрицательна на (1;3) г) нули производной функции 1 д) нули функции -2 и 2


    Решение: 1). Область определения функции есть промежуток [-3; 4];
    2). Значение функции составляет промежуток [-4; 3];
    3). Функция убывает на промежутке [-3; 1]и возрастает на промежутке
    [1; 4];
    4). Значения функции отрицательны только в точках промежутка (-1;2).

    _____________________________________________

    . Область определения функции есть промежуток - . Значение функции составляет промежуток - . Функция убывает на промежутке - и возрастает на промежутке . Значения функции отр...

  • Исследование функции с помощью произвоной
    y=(x+2)^3/(x-1)^2
    1) Найти область определения функции
    2) Чётность, нечётность функции
    3) Непрерывность
    4) Критические точки
    5) Интервалы возрастания и убывания функции
    6) Экстремумы функции
    7) Критические точки второго рода
    8) Интервалы выпуклости и вогнутости функции
    9) Точки перегиба
    10) Асимптоты
    11) Построить график


    Решение: y=(x+2)^3/(x-1)^2
    1) Найти область определения функции
    выражений с корнем четной степени нет
    знаменатель не равен нулю, значит х-1 не равен 0 значит х - не равен 1
    область определения х є (-беск;1) U (1:+беск)
    2) Чётность, нечётность функции
    y(x)=(x+2)^3/(x-1)^2
    y(-x)=(-x+2)^3/(-x-1)^2 не равно y(x)
    y(-x)=(-x+2)^3/(-x-1)^2 не равно -y(x)
    y(x)=(x+2)^3/(x-1)^2 не является ни четной ни нечетной
    3) Непрерывность
    y(x)=(x+2)^3/(x-1)^2 имеет точку разрыва при х=1
    4) Критические точки
    y(x)=(x+2)^3/(x-1)^2
    y’(x)={3*(x+2)^2*(x-1)^2-(x+2)^3*2*(x-1)}/(x-1)^4 =
    ={3*(x-1)-2*(x+2)}*(x+2)^2/(x-1)^3=
    =(3x-3-2x-4)*(x+2)^2/(x-1)^3=
    =(x-7)*(x+2)^2/(x-1)^3
    y’(x)=0 при
    (x-7)*(x+2)^2/(x-1)^3=0
    х=-2 x=1 х=7 - критические точки
    5) Интервалы возрастания и убывания функции
     в точках x=1 и х = 7 производная меняет знак
    интервалы возрастания
    х є (7; +беск) U (-2;1) U (-беск ;-2)
    интервалы убывания
    х є (1;7)
    6) Экстремумы функции
     в точках x=1 и х = 7 производная меняет знак
    x=1 - локальный максимум
    х = 7- локальный минимум
    7) Критические точки второго рода
    x=1  - критические точки 2 рода
    8) Интервалы выпуклости и вогнутости функции
    надо считать вторую производную - лень
    9) Точки перегиба
    то же самое
    10) Асимптоты
    вертикальная асимптота у=1
    наклонная асимптота ищем в виде
    у=ах+в
    а = lim(y)/x=1
    b=lim(y-a*x)=8
    асимптота у = х+8
    11) Построить график
    график

<< < 192021