график функции »

область определения функции - страница 20

  • 1. функция задана формулой:
    f(x) = 2х^2 - х + 1. Найдите
    f(-1)
    2. Определите корни
    квадратного трехчлена:
    x^2 -2х-15
    3. Решите уравнение у^2 - 2у^2-3=0


    Решение: 1. f(-1) = 2*(-1)² - (-1) + 1 = 2*1 +1 +1 = 4
    2. x² - 2x - 15 = 0 | a =1; b =-2; c =-15
    D = b² - 4*a*c = 4 + 60 = 64
    x₁ = (-b - √D) / 2 = (2 - 8) / 2 = -3;
    x₂ = (-b + √D) / 2 = (2 + 8) / 2 = 5.
    Ответ: - 3; 5.
    3. y^4 - 2*y² - 3 = 0
    Пусть y²= t
    t² - 2*t - 3 = 0
    D = 4 +12 = 16
    x₁ = (2 - 4) /2 = -1
    x₂ = (2 + 4) /2 = 3
    x² = -1
    Корней нет
    x² = 3
    x₁ = √3
    x₂ = -√3
    Ответ: -√3; √3.

  • Исследуйте функцию y=6x^2 - x^3 - 8
    и постройте ее график.
    Для этого найдите :
    а) область определения D(y)
    б) производную и критические точки
    в) промежутки монотонности
    г) точки экстремума и экстремумы
    д) точку пересечения с осью Oy и несколько точек графика
    е) множество значений E(y) функции
    ж) корни функции ( можно приближенно )


    Решение: функция определена на всей числовй оси

    y’=12x-3x^2

    y’=0 12x-3x^2=0  3x(4-x)=0  x=0  x=4

    y’’=12-6x=0

    x=2 y(2)=24-8-8=8

    (2;8) точка перегиба

    y’’(0)>0 точка минимума (0;-8)

    y(4)=6*16-8-4*16=24

    (4;24) точка максимума

    при x<0 x>4 функция убывает

    при 0<x<4 -функция возрастает

    нули (0;-8)

    корни x1=-1,1 x2=1,3  x3=5,8

  • Функция задана графиком. Назвать:
    1) область определения функции
    2) область значения функции
    3) f наибольшим и f наименьшим 4) промежутки возрастания и убывания
    5) нули функции
    6) является функция четный или нечетный 7) при каких значениях аргумента f(x) больше 0? И f(x) меньше 0?


    Решение: 1) область определения функции [-2;4]
    2) область значения функции [-3;4]
    3) f наибольшим и f наименьшим y(0)=y(4)=4 максимум y(-2)=-3 y(2)=-2
    4) промежутки возрастания и убывания убывает (0;2) возрастает (-2;0) U (2;4)
    5) нули функции (-1;0) (1;0) 3;0) (0;4)
    6) является функция четный или нечетный функция не обладает данным свойством
    7) при каких значениях аргумента f(x) больше 0? И f(x) меньше 0?
    (-1;1) U x>3 f(x)>0
    [-2-1) U (1;3) f(x)<0

  • Функция задана графиком. укажите формулу, которая задаёт функцию


    Решение: График данной функции находится во 2-ой и 4-ой четверти.
    Значит угловой коэффициент графика - меньше 0 (k<0).
    Следовательно нам подходят только 2) у=-3х и 3) у=-2х.
    Если присмотреться внимательно к графику, то можно заметить что он проходит через точку (1; -3). Подставим эту точку в оба графика.
    2) у=-3х
    (1; -3)
    -3=-3*1
    -3=3 значит точка принадлежит графику
    3) у=-2х
    (1;-3)
    -3=-2*1
    -3≠-2 точка не принадлежит графику
    Ответ график 2) у=-3х 

  • Квадратичная функция
    №2. Функция задана формулой у = 3х2 + 2х – 5.
    а) Найдите значение функции при х =
    б) Найдите нули функции.
    №3. а) Постройте график функции у = -х2 + 4.
    б) Укажите значение аргумента, при которых функция принимает отрицательные значения.
    в) Укажите промежуток, на котором функция убывает.
    №4. Решите неравенство х2 – 3х +2
    №5. Запишите уравнение параболы, если известно, что она получена сдвигом параболы у = 2х2 вдоль оси Х на четыре единицы вправо и вдоль оси У на две единицы вниз.
    №6. Найдите область определения функции у =.
    №7. При каких значениях p и q вершина параболы y = x2 + pх + q находится в точке (-1; 5)


    Решение: №2. y=3x²+2x-5
    а)x=-2/3 => y=3*(-2/3)² + 2*(-2/3)-5 = 3*4/9 - 4/3 - 5 = 4/3 - 4/3 - 5 = -5;
    y=-5;
    б)0=3x²+2x-5
    D=b²-4ac, D=2² - 4 * 3 * (-5)=64;
    x1=(-b-√D)/2a, x2=(-b+√D)/2a
    x1=(-2-8)/2*3=-5/3;
    x2=(-2+8)/2*3=1.
    x1=-5/3 и x2=1- нули функции.
    №3 К этому номеру будет фотография (а)
    б) при х∈(-∞;-2)∪(2;+∞);
    в) функция убывает при x∈[0;=∞).
    №4 x²-3x+2
    Приравняю к нулю =>  x²-3x+2=0;
    D=b^2-4ac,
    D=(-3)²-4*2*1=1;
    x1=(-b-√D)/2a, x2=(-b+√D)/2a
    x1=(3-1)/2*1=1, x2=(3+1)/2*1=2
    Ответ: 1;2.
    №5 y=2(x-4)²-2
    1)y=ax²+n получен из y=ax² параллельным переносом вдоль оси Oy на n единиц вверх (при n>0) и на n единиц вниз (при n<0).2)y=a(x-m)² получен из y=ax² параллельным переносом вдоль оси Ox на m единиц вправо (при m>0) и на m единиц влево (при m<0).
    №6 Ты мне сказал не решать.
    №7 в-вершина, xв=-1, yв=5;
    y=x²+px+q;
    xв=-b/2a=-p/2;
    -p=xв*2;
    -p=-1*2=-2;
    p=2;
    Подставим все имеющиеся переменные в функцию y=x²+px+q:
    5=(-1)²+2*(-1)+q;
    5=1-2+q;
    5=q-1;
    q=5+1=6
    Ответ: при p=2 и q=6 вершина параболы y = x2 + pх + q находится в точке (-1;5).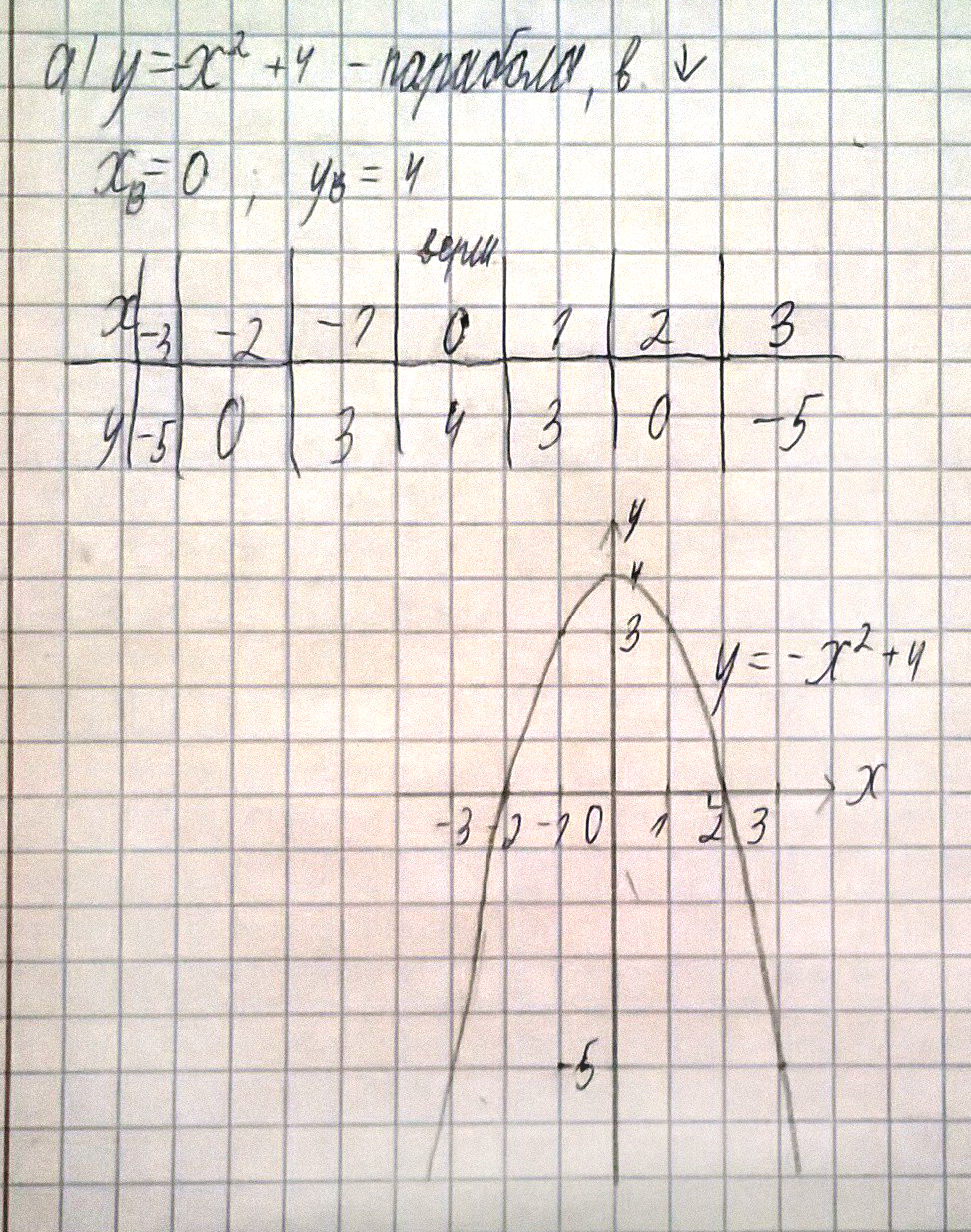

    . y x x- а x - y -     - -      -   -       -   -     - y - б x x- D b - ac D  -          - x -b- D a x -b D ax - - - x - .x - и x - нули функции. К этому номеру будет фотогр...
<< < 181920 21 > >>