график функции »

область определения функции - страница 18

  • №1 (Найдите значение дроби):
    а) 12у+3у2 (игрик в квадрате) - в числителе
    (4у+у2, т. е. игрик в квадрате)(у-0.4)- в знаменателе.
    При у=1.9
    б) n2-64 - в числителе
    n2+64+16n - в знаменателе
    При n=12
    №2( Найдите естественную область определения рациональной дроби):
    а) 3х - в числителе
    9х+15 - в знаменателе
    б) 11 - в числителе
    2m(m-5) - в знаменателе
    №3 Сократите дробь 6abd - в сислителе
    bdc-abd- в знаметателе
    Хоть что-нибудь))


    Решение: №1 
    а) 12у+3у^2 = 3у(4+у) =   3 =   3 =   3 = 30 = 2
    (4у+у^2)(у-0.4) у(4+у)(у-0,4) у-0,4 1,9-0,4 1,5 15
    б) n^2-64 =(n-8)(n+8) =  n-8 = 12-8 = 4 = 1
      n^2+64+16n (n+8)^2 n+8 12+8 20 5
    №2( Найдите естественную область определения рациональной дроби):
    а) 3х 
    9х+15 9x+15 не равно 0

      9х не равно -15

      х не равен -15/9 = -5/3
    б) 11
    2m(m-5)  m не равно 0,  m не равно 5
    №3 6abd = 6abd = 6a
      bdc-abd bd(c-a) c-a

  • Найдите наибольшее значение дроби
    30/16х^2+6-24ху+9у^2
    найдите область определения функций
    у=3(х-6)-х+2/х(х+4)


    Решение: $$ \frac{30}{16x^2+6-24xy+9y^2}=\frac{30}{(4x-3y)^2+6} $$
    Дробь принимает наибольшее значение, когда знаменатель принимает своё наименьшее значение. Это будет тогда, когда первое слагаемое будет =0.
    $$ (4x-3y)^2=0\to (4x-3y)^2+6=6\\\frac{30}{6}=5 $$ 
    Наибольшее значение дроби равно 5.
    2) ООФ: знаменатель дроби не=0.
    х(х+4) не=0,> х не=0, х не=-4
    х Є (-беск,4)U(-4,0)U(0, беск) 

  • 1) В какой координатной четверти расположена вершина параболы?
    y=6x^2-x-25
    2) в каких координатных четвертях расположен график?
    y=-1,6/x(дробь)
    3) решите уравнение
    4x^2-5x^2+1=0
    4) Найдите область определения функции
    y=под корнем 12-8x-x^2
    5) найдите множество решений неравенства
    (x^2-16)(x-5)<0


    Решение: 1) Найдём координаты вершины:

    x=-b/2a=1/12

    $$ y=6*1/144 - 1/12-25=1/24-1/12 -25=-1/24 -25=-25\frac{1}{24} $$

    В четвертой четверти

    3) $$ 4x^{2} - 5x^{2}+1=0 \\ 1-x^{2}=0 \\ (1-x)(1+x)=0 \\ x=1 x=-1 $$

    4)$$ 12-8x-x^{2}\geq0 \\ x^{2}+8x-12\leq0 \\ D=64+48=112 \\ x_{1}=(-8+\sqrt{112})/2 \\ x_{2}=(-8-\sqrt{112})/2 $$

    Х принадлежит от $$ [(-8-\sqrt{112})/2; (-8+\sqrt{112})/2] $$

    5) $$ (x^{2}-16)(x-5)<0 \\ (x-4)(x+4)(x-5)=0 \\ x=4; x=-4; x=5 \\ X=(\infty;-4) $$

  • 1.) Решите графически уравнение 6-х-х2(кв.)=0.
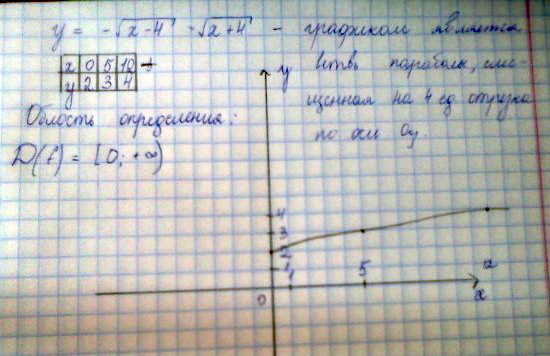
    2) Постройте график функции y=-под корнем x-4.(Под одним корнем x-4) Укажите область определения функции.


    Решение: 1)6-х-х2(кв.)=0;

    -х2(кв.)-х+6=0;

    это уравнение можно умножить на -1, так легче счетать и получится х2(кв.)+х-6=0

    D= -1 (кв.)-4*(-1)*24= 1+24=25

    х1= (1-5):2*(-1)= -4:(-2)=2; х2=(1+5):2*(-1)=6:(-2)=-3

    2)

    -х-х кв. -х кв. -х это уравнение можно умножить на - так легче счетать и получится х кв. х- D - кв. - - х - - - - х - - -...

  • Исследуйте функцию по общей схеме и постройье график.
    1. Область определения функции, точки разрыва.
    2. Корни функции (нули).
    3. Четность (нечетность).
    4. Периодичность.
    5. Промежутки монотонности и точки экстреумума (следуйте алгоритму):
    Найдите y’(x)
    1. Определитель критические (стационарные) точки.
    2. Опрежелите знаки y’(x) в достаточно малых окрестностях найденных критических точек и точек разрыва функции y=y(x).
    3. Заполните таблицу:
    X ?
    Y’ ?
    Y ?
    6. Промежутки выпуклости (вогнутости), точки перегиба.
    7. Асимптоты.
    8. Построение графика.
    y=((x-1)^3)-3(x-1)


    Решение: Y=(x-1)(x²-2x+1-3)=(x-1)(x²-2x-2)
    D(y)∈(-∞;∞)
    Aсимптот нет
    Непериодична
    y(-x)=(-x-1)(x²+2x-2) ни четная, ни нечетная
    x=0  y=2
    y=0  x=1;x=1-√3;x=1+√3
    Точки пересечения с осями (0;2);(1;0);(1-√3;0);(1+√3;0)
    y’=1*(x²-2x-2)+(x-1)(2x-2)=x²-2x-2+2x²-4x+2=3x²-6x=0
    3x(x-2)=0
    x=0 u x=2
       + _ +
    -(0)-(2)-
    возр max убыв min  возр
    ymax=2
    ymin=-2
    y’’=6x-6=0
    x=1
    y(1)=0-точка перегиба
      _ +
     -(1)-
    выпук вверх вогн вниз 

<< < 161718 19 20 > >>