график функции »

область определения функции - страница 19

  • Построить график функции y=x^2+3x+4+(x+4)/(x+4)+корень из(x+4) - корень из (x+4).


    Решение: $$ y= x^{2} +3x+4+ \frac{x+4}{x+4} + \sqrt{x+4} - \sqrt{x+4} $$
    ОДЗ: х+4≥0, х≠-4 ⇒ (- 4;+∞)
    Выделим полный квадрат:
    $$ y=(x+ \frac{3}{2} ) ^{2} - \frac{9}{4} +4, \\ y=(x+ \frac{3}{2}) ^{2} + \frac{7}{4} $$
    Осталось построить эту параболу на (- 4;+∞)
    Вершина параболы в точке (-3/2; 7/4). парабола пересекает ось Оу в точке (0;4)
    Дополнительные точки (-4;8) и (-1;8)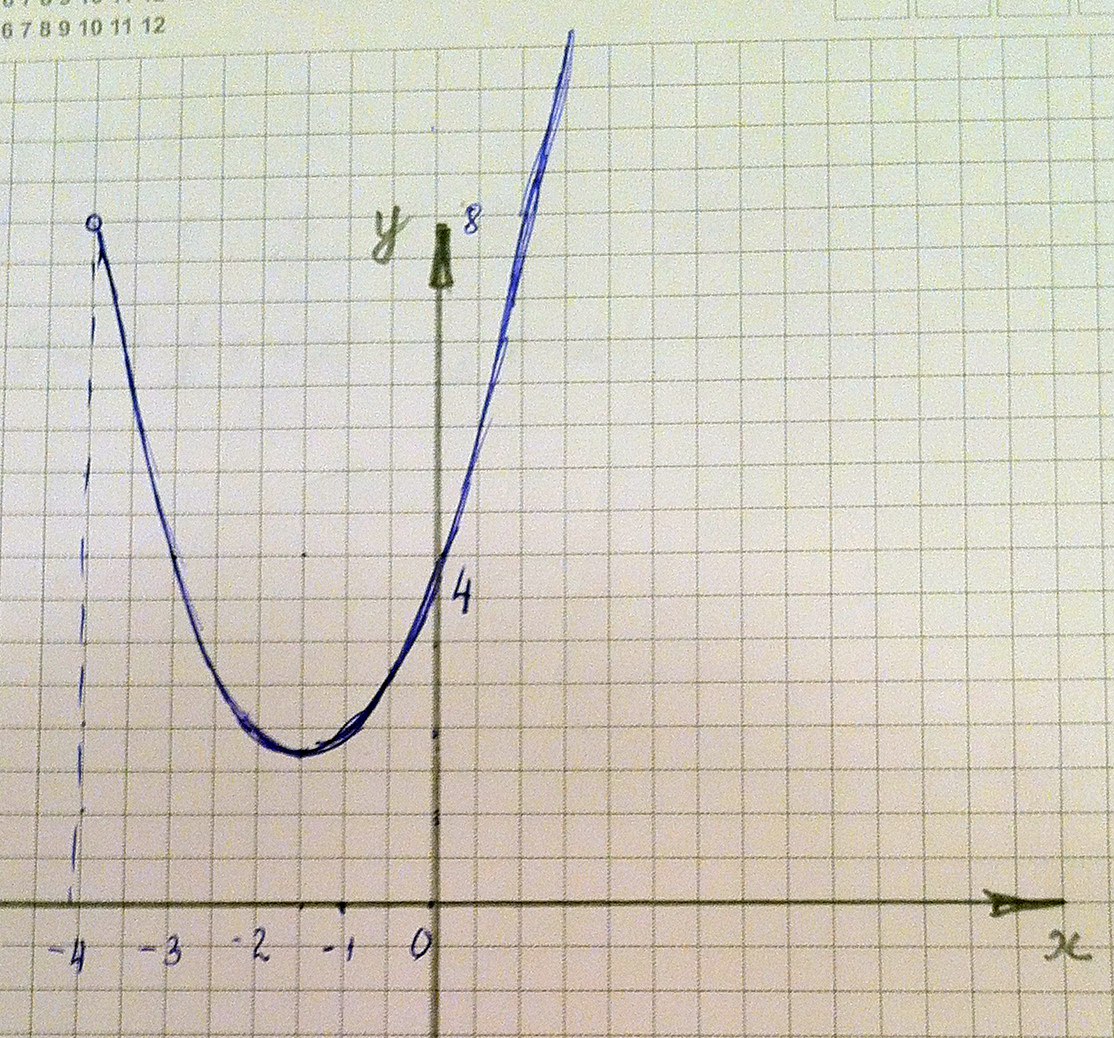

    y x x frac x x sqrt x - sqrt x ОДЗ х х - - Выделим полный квадрат y x frac - frac y x frac frac Осталось построить эту параболу на - Вершина параболы в точке - . парабола пер...


  • 1. Начертите график функции y=корень из x. Какова область определения этой функции.
    2. Принадлежит ли графику функции y в квадрате = корень из x A(121:11) B(-81:9)
    3. Сколько корней имеет уравнение x в квадрате =а ; взависимости от значения А


    Решение: Выражение под корнем больше или равно 0x^2-3*x -4 >=0решаем квадратное уравнение:x^2-3*x -4 =0D=9-4*(-4)=25корень из D =5x1 = (3+5)/2=4,x2=(3-5)/2=-1рисуем ось х, отмечаем на ней 2 точки( закрашенные) -1 и 4в промежутке [-беск.;-1]  выражение будет положительным. нужно просто подставить в уравнение число из промежутка, в [-1: 4 ] отрицв [4: беск] полож.=> выбираем промежутки, где ф-я принимает полож значение[-беск.;-1] и  [4: беск]

  • Постройте график линейной функции y=0.5x-3. Используя график функции определите a) y, если x=-3 ;8 б) x, если y=-1 ;-2 в) область определения и область значение функции г) корни функции д) интервалы, в которых функция положительная и отрицательная е) интервалы, в которых функция возрастает и убывает


    Решение: Таблица для черчения графика: x 2   4   6

                                                      y -2  -1  0

    А) х=-3 у=-4.5 \ х=8 у=1

    Б) у=-1 х=4 \ у=-2 х=2

    В) ООФ (-бескон.;+бескон.) ООЗ тоже самое

    Г)(-бескон;+бескон.)

    Д) Положительная (6;+бескон.)

        Отрицательная (-бескон.;6)

    Е) Возрастает (-бескон.; +бескон.)

        Не убывает.

  • 1. Постройте график функции y=3/x. Укажите промежутки возрастания и убывания функции.
    2. Упростить выражение: cos(x-y)-cosx*cosy
    3. Найдите a1 и d арифметической прогрессии (an), если а10=39.5, а а3=4.5
    4. Решить систему уравнений: {x^2-y=21
    {x+y=9
    5. Найти область определения функции: y=√-36-x^2+12x (выраж. под корнем)
    6. На пост депутата маслихата претендовало три кандидата: Ахметов, Бакиев, Утешев. Во время выборов за Утешева было отдано в 1.5 раза больше голосов, чем за Ахметова, а за Бакиева - в 4 раза больше, чем за Ахметова и Утешева вместе. Сколько процентов избирателей проголосовало за победителя?


    Решение: 1. просто подставьте х=-1 х=1 х=1.5 х=-1.5 х=3 х=-3 х=9 х=-9
    2.
    cos(x-y)-cosx*cosy=cos(x-y)-cos(x*y)=cos((x-y)*xy)=cos(x^2y-xy^2)
    3. а10=а3+7d
    7d=a10-a3
    7d=39.5-4.5=35
    d=35:7=5
    a3=a1+2d
    a1=a3-2d
    a1=4.5-2*5=4.5-10=-5.5
    Ответ: d=5, a1=-5.5
    4.{х^2-у=21
    {х+у=9
    х^2+х=30
    х^2+х-30=0
    D=1^2-4*1*(-30)=1+120=121
    √D=11
    x1=(-1+11)/2=10/2=5
    x2=(-1-11)/2=-12/2=-6
    Если х=5, то х+у=9
    У=9-х
    У=9-5
    У=4
    если х=-6, то у=9-(-6)
    У=9+6
    У=15
    Ответ: (5;4) ; (-6;15)
    6. пусть за Бакиева проголосовало х человек, тогда за Утешева и Ахметова проголосовало х/4
    х+х/4=100
    4х+х=400
    5х=400
    х=80
    80 % людей проголовали за победителя
    Ответ: 80%

  • 1. Найти область определения функцииf(x) = Под корнем 5x-25
    2. Для функции y=f(x) найти значения x, когда y=x^3 - x a) y = 0, б)y>0; в)y<0
    3. Исследователь на четность функциюf(x) = -4x^4 + x^2
    4. Построить график функции.y=x^2 - 4
    5. Изобразить график непрерывной функции y=f(x), зная, что:a) D (y) = [-1;6]b) E (y) = [-4;3]в) y>0 только на (0:3); г) y возрастает на [-1;2] у убывает на [2;6]


    Решение: 1. $$5x-25 \geq 0 \\ 5x \geq 25 \\ х \geq 5$$ответ:$$ х \geq 5$$
    2. Для функции y=f(x) найти значения x, когда y=x^3 - x
    решение:
    а)x^3 - x=0
    x(x^2-1)=0
    x=0 х=1 х=-1
    ответ:x=0 х=1 х=-1
    б)x^3 - x>0
    x(x^2-1)>0
    x принадлежит (-1;0)U(1;+ бескон.)
    ответ:x принадлежит (-1;0)U(1;+ бескон.)
<< < 171819 20 21 > >>