координаты »

найти координаты точки пересечения прямых - страница 2

  • Найти координаты точки пересечения прямых
    Y1=4x+11
    Y2=8x-1


    Решение: У=4Х+11; (1)

    У=8Х-1; (2)

    2: 4Х+11=8Х-1;

    4Х=12;

    Х=3;

    1: У=23.

    ОТВЕТ: (3;23).

    y₁ = 4x +11

    y₂ = 8x -1

    Пусть точка пересечения прямых имеет координаты (x₀ ; y₀ ),

    тогда выполняются равенства:

    y₀ = 4x₀ +11

    y₀ = 8x₀ -1

    левые части уравнений равны  =>  равны и правые части,  т. е.

    8x₀ -1 = 4x₀ +11

    8x₀ - 4x₀ =  11 + 1

    4x₀ =  12

    x₀ = 3

    Теперь подставив значение x₀  в любое из уравнений, получим y₀ :

    y₀ = 4x₀ +11 = y₀ = 4*3 +11 = 12 +11 = 23

    Итак, координаты точки пересечения прямых ( 3 ; 23)

    Ответ:  ( 3 ; 23).

  • Решить:
    Найти координаты точки пересечения прямых y=5x−7 и y=x+5


    Решение: Давайте сначала подумаем. Почему прямые пересекаются? Потому, что имеют общее решение. То есть, существует пара точек, аргумент и значение функции, обращающие каждую формулу в верное равенство.
    А почему 1 решение? Пересечение бывает только раз.
    Приравниваем y.
    5х-7=х+5
    4х=12
    х=3
    Дальше аргумент в любую функцию подставляете, какая вам нравится.
    Пусть: y=5*3-7, откуда y = 8
    Ответ:(3;8)

  • 1) построить график линейной функции у=-2х+1. С помощью графика найти: а) наименьшее и наибольшее значение функции на отрезке [-1;2]. б) значения переменной х, при которых график функции расположен ниже оси Ох.
    2) Найти координаты точки пересечения прямых у= 3 -х и у = 2х


    Решение: а) у наменьшее -3 при х=2 ; у наибольшее 3 при х=-1
      б) х>2
    №3 а) -3х+2у-6=0 
      2у=6+3х
      у=(6+3х)2
      у=3+1,5х
    линейная функция пересекается с осью Ох в точке ( -2;0)
    линейная функция пересекается с осью Оу в точке (0;3)
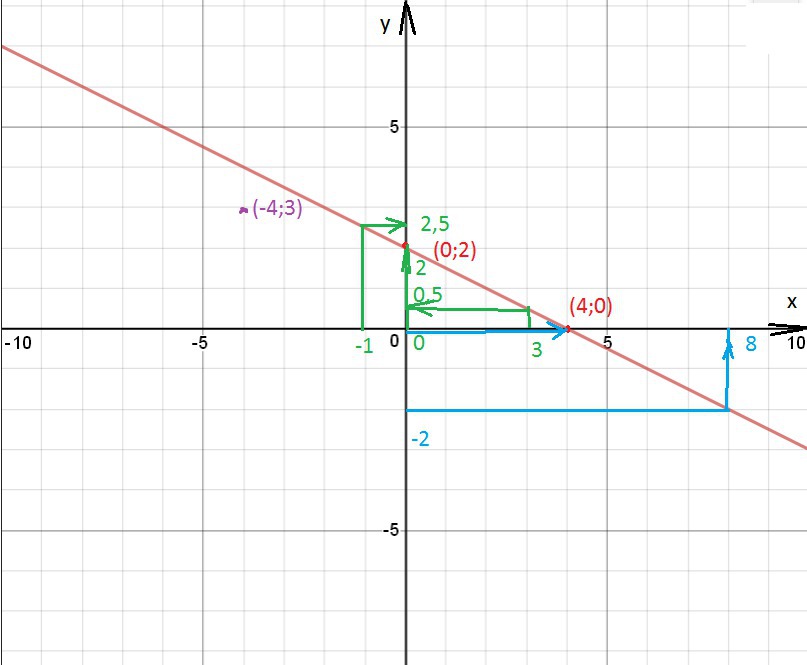
    б) точка К не принадлежит графику данного уравнения

  • 1. Построить график функции у = -0,5х + 2. По графику найти:
    а) значение функции, если значение аргумента равно -1; 0; 3;
    б) значение аргумента, если значение функции равно -2; 0; 2;
    в) координаты точек пересечения прямой с осью х и с осью у;
    г) принадлежит ли графику функции точка (-4;3)?
    2. Найти координаты точки пересечения прямых у = -х и у = -2х +1 графическим и аналитическим методами


    Решение: 1. См. рисунок 1.
    а) при х=-1 у=2,5
        при х=0  у=2
       при х=3  у=0,5
    б) при у=-2 х=8
       при у=0 х=4
       при у=2 х=0
    в) с осью Ох точка (4;0)
      с осью Оу точка (0;2)
    г) не принадлежит
    2.  Приравниваем левые части
       -х=-2х+1
       2х-х=1
       х=1
    тогда у =-х
       у =-1
    О т в е т. (1;-1)
    Графическое решение см 2.

    . См. рисунок .а при х - у     при х   у    при х   у б при у - х    при у х    при у х в с осью Ох точка   с осью Оу точка г не принадлежит .  Приравниваем левые части   -х...

  • даны точки A(4;4),B(-1;6),C(0;2),D(3;2). найти координаты точки пересечения прямых AC и BD


    Решение: 1) Составляем уравнение AC: 
    (x-xA)/(xC-xA)=(y-yA)/(yC-yA) 
    (x-4)/(0-4)=(y-4)/(2-4) 
    (x-4)/(-4)=(y-4)/(-2) 
    x-4=2(y-4)
    x-4=2y-8

    x=2y-8+4

    x=2y-4
    2) Составляем уравнение BD: 
    (x-xB)/(xD-xB)=(y-yB)/(yD-yB) 
    (x+1)/(3+1)=(y-6)/(2-6) 
    (x+1)/4=(y-6)/(-4) 
    x+1=-(y-6)

    x+1=-y+6

    x=5-y
    3) Находим точку пересечения диагоналей АС и BD: 
    2y-4=5-y

    3y=9

    y=3
    x=5-3=2 
    Ответ: О(2; 3)

<< < 12 3 > >>